第二篇 计算机是如何学会下棋的（五）
清华大学计算机系 马少平
第五节：AlphaGo是如何下棋的
艾博士继续讲到：蒙特卡洛树搜索方法于2006年被应用于计算机围棋中，使得计算机围棋的水平有了质的飞跃，可以达到业余中高手的水平，可以说是计算机围棋发展史上的一个里程碑。但是，距离职业棋手的水平还有很大差距，经历了一段时间的发展后，很快又进入停滞期，水平很难再次提高。
小明问：这是为什么呢？从原理上来说蒙特卡洛树搜索方法是个很靠谱的方法啊。
艾博士解释说：依靠随机模拟的方法估算概率必须有足够的模拟次数，由于围棋可能的状态数太多，虽然在蒙特卡洛树搜索中通过信心上限有选择地做模拟，但是模拟的还是有些盲目，没有利用到围棋本身的一些特性或者知识，在规定的时间内模拟次数不够，估算的概率不够准确，从而影响了计算机围棋的水平。
小明：如何解决这个问题呢？
艾博士：取得突破的就是AlphaGo了。AlphaGo将深度学习方法，也就是神经网络与蒙特卡洛树搜索有效地结合在一起，巧妙地解决了这个问题。
小明：AlphaGo是如何解决的呢？
艾博士：小明还记得前面我们分析为什么以前的计算机围棋水平比较低？
小明想了想回答说：艾博士，您讲了几条原因，第一条说的就是局势评估问题，但是局势评估采用蒙特卡洛树搜索方法已经解决了，您问的应该不是这个问题。我猜想是您最后提到的有关逻辑思维、形象思维问题，您提到人在下围棋的过程中用到的更多的是形象思维，而不是逻辑思维。
艾博士：小明说的非常正确。长期以来一直认为计算机更擅长处理逻辑思维问题，而不擅长处理形象思维问题，但是深度学习方法的提出改变了这一看法，利用深度学习也可以很好地处理一些形象思维的问题，如图像识别等。围棋的棋局看起来更像一幅图像，所以可能更适合用深度学习方法处理，通过深度学习方法从围棋棋谱中学习围棋知识，与蒙特卡洛树搜索结合在一起，提高蒙特卡洛树搜索的效率和随机模拟的准确性。
小明：这倒是一个很好的思路，AlphaGo究竟是如何做到这点的呢？
艾博士：在此想法的指导下，AlphaGo构建了两个神经网络，一个是策略网络，一个是估值网络。我们先介绍这两个神经网络的功能以及具体的实现方法。
策略网络由一个神经网络构成，其输入是当前棋局，输出则是每个可下棋点的行棋概率，行棋概率越大的点，越说明这是一个好的可下棋点，应该优先选择在这里行棋。
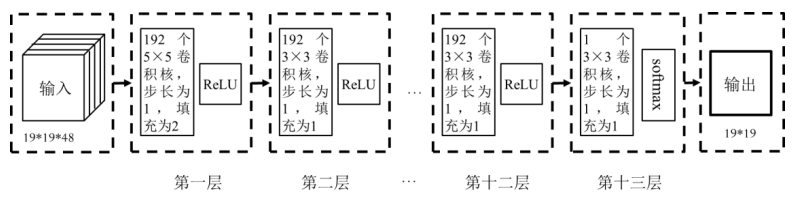
图2.14 AlphaGo策略网络示意图
图2.14给出了AlphaGo的策略网络示意图。输入是由48个大小为19×19的通道表示的当前棋局。
小明问到：我知道大小19×19是因为围棋的棋盘是19×19的，但是为什么有48个通道呢？
艾博士解释说：每个通道用来表示当前棋局的一些特征。比如：一个通道是当前棋局有我方棋子的位置为1，其他位置为0；一个通道是当前棋局有对方棋子的位置为1，其他位置为0；还有一个通道是当前棋局中没有落子的位置为1，其他位置为0。用8个通道分别表示当前棋局中一个棋链所具有的气数，这里的棋链可以理解为连接在一起的相同颜色的一块棋。比如一个棋链的气数是5，则在气数为5的通道中用1表示，其他位置为0。这样8个通道分别表示气数1到气数8。
小明听的有些迷糊，问艾博士：什么叫棋链的气数啊？
艾博士回答说：气数是围棋中一个很重要的概念，涉及到围棋知识，我们就不详细介绍了。还有8个通道记录最近的8个棋局。其余的几个通道我们就不具体说了，都与围棋知识有关。类似的特征共用了48个通道表示。
小明：输入竟然这么详细。
艾博士：接下来就是一个普通的卷积神经网络了，不知小明是否还记得卷积神经网络的相关内容，如果记不清楚了请复习我们前面讲过的第一篇内容“神经网络是如何实现的”。
小明：艾博士，我记得呢，听您讲完后我还认真复习了呢。
艾博士夸奖说：小明真是一个好学生。
艾博士：第一个卷积层由192个5×5的卷积核组成，步长为1，填充为2，接ReLU激活函数后，得到192个19×19的通道。第二层到第十二层都是一样的，每层192个3×3卷积核，步长为1，填充为1，接ReLU激活函数。第十三层是1个3×3的卷积核，步长为1，填充为1，接softmax激活函数，得到策略网络最终大小为19×19的输出，输出值范围为0到1之间，表示棋盘上每个点的行棋概率。
小明问：棋盘上有些地方已经有棋子了，已经有棋子的地方是不能再落子的，为什么输出是19×19、是整个棋盘呢？
艾博士解释说：神经网络本身是很难做出这些判断的，在使用策略网络的输出结果时，会专门用程序判断一下，剔除这样的点。
小明问：程序判断一下倒是比较容易。怎么获得策略网络的训练数据呢？
艾博士：在AlphaGo中共用了16万盘人类棋手棋谱进行训练，棋谱的每一步行棋都可以作为一个训练样本。策略网络的目标就是学会“像人类那样下棋”。所以如果棋谱中人类棋手在a处走了一步棋，则可以认为在a处下棋的概率为1，我们用 ta 表示。如果用 pa 表示策略网络给出的在a处下棋的概率，则 pa 应该逼近ta 。由于两个表示的都是概率，所以损失函数可以采用交叉熵损失函数，即：
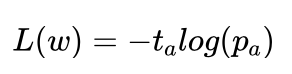
这样我们就可以通过逐步优化该损失函数，使得策略网络的性能逐步逼近人类棋手的目的。
小明：如果只是逼近人类棋手，如何做到战胜人类围棋高手呢？
艾博士：首先这种逼近是对16万盘人类棋谱的逼近，可以说是扬长避短，吸取了众多高手之精华。其次，后面我们还要讲到，AlphaGo是将策略网络等与蒙特卡洛树搜索融合在一起，通过大规模的随机模拟选取一个最佳走步，这相当于起到了一个“智力放大”的作用，这可能才是AlphaGo强大的真正原因。
小明：艾博士这么一讲解，就明白怎么训练了，其实跟神经网络用于图像分类原理是一样的，当前棋局相当于图像，在哪个位置行棋相当于类别标记。
艾博士：对，就是相当于一个分类问题。所以说在求解一个新问题时，要看看是否能套到一个已知问题上，如果可以的话，就可以用已有的办法求解了。
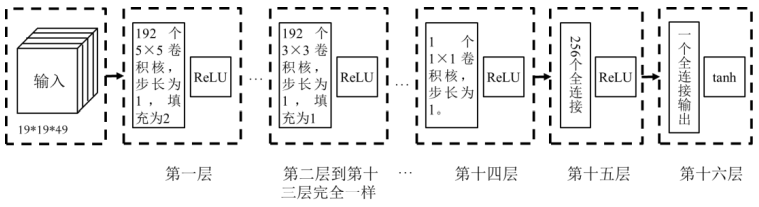
图2.15 AlphaGo估值网络示意图
下面再介绍AlphaGo用到的另一个神经网络——估值网络。估值网络对当前棋局进行评估，输入是当前棋局，输出是一个在-1和1之间的数值，表示棋局对当前执子方的有利程度即收益。当数值大于0时，表示对当前执子方有利，而小于0是表示对对方有利。
图2.15给出了估值网络的示意图。输入为49个大小为19×19的通道，其中前48个通道与策略网络的通道是一样的，但是比策略网络多了一个与当前执子方有关的通道，如果执子方为黑棋，则该通道全部为1，否则全部为0。估值网络共由16层组成，其中第一层为192个5×5的卷积核，步长为1，填充为2，后面接ReLU激活函数。第二层到第十三层是完全一样的，每层为192个3×3的卷积核，步长为1，填充为1，后面接ReLU激活函数。第十四层为1个1×1的卷积核，步长为1，后面接ReLU激活函数。第十五层为含有256个神经元的全连接层，每个神经元接ReLU激活函数。第十六次为只有一个神经元的全连接层，该神经元接tanh激活函数，得到取值在-1和1之间的整个神经网络的输出。
估值网络的训练样本同样来自16万盘人类棋手的棋谱，一盘棋出现的所有棋局作为训练样本，获胜方的棋局标签为1，失败方的棋局标签为-1。估值网络的目标就是预测一盘棋的胜负，对我方占优的局面，其输出值应该接近于1，对对方占优的局面，其输出应该接近于-1。为此损失函数可以采用误差的平方。具体的损失函数如下：
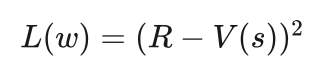
其中s表示棋局即输入的样本，R为该局棋的胜负情况，获胜R取值为1，失败取值为-1，V(s)为估值网络的输出。
小明听着艾博士的讲解领悟到：如果熟悉了神经网络，策略网络和估值网络看起来并不难。
艾博士：确实是这样的，无论是策略网络还是估值网络，其实就是一个普通的卷积神经网络。其实也不是AlphaGo第一次将神经网络用于围棋中，以前也有团队曾经做过尝试。AlphaGo的主要贡献是将神经网络与蒙特卡洛树搜索巧妙地结合在一起，这才有了战胜人类最高水平棋手的能力。
小明：AlphaGo是怎样将神经网络和蒙特卡洛树搜索结合在一起的呢？
艾博士：在蒙特卡洛树搜索中最主要的就是如何选择待模拟的节点，小明还记得如何选择吗？
小明想了想说：优先选择信心上限最大的节点，该策略同时考虑了收益和模拟次数两方面的因素，第j个落子点的信心上限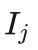 
计算公式如下：
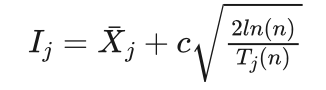
其中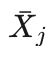 
是落子点j的平均收益，
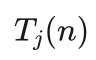是落子点j的模拟次数，n是j的父节点的模拟次数，c为加权系数。
艾博士：小明你记得很清楚。在蒙特卡洛树搜索中，收益值是通过随机模拟获得的，被选择模拟的次数越多其收益值越准确。一方面，信心上限策略对于已经被选择过多次的节点，其收益值已经比较可信，倾向于选择收益最好的节点，以便进一步确认其收益值。另一方面，对于被选择次数比较少的节点，其收益值的多少并不可信，希望再多被选择几次，以便提高其收益值的准确性。在AlphaGo中又增加了第三个原则，策略网络会提供每个可落子点的概率，具有高概率的可落子点应该是一个比较好的走步，希望具有高概率的可落子点被优先选择。
为此AlphaGo对信心上限的计算做了修改，以便更多地利用策略网络和估值网络的结果，因为这两个网络是从人类棋手的棋谱中学到的，有理由相信这两个网络的计算结果，但其基本思想并没有改变，还是同时考虑收益和模拟次数两方面的因素，只是引入了更多的量。
小明：都引入了哪些量呢？
艾博士：对于一个棋局s，我们可以从两个途径获得其收益，一个途径是通过估值网络获得，用value(s)表示，另一个途径是通过随机模拟获得，用rollout(s)表示。我们用二者的加权平均作为棋局s第i次模拟的收益：
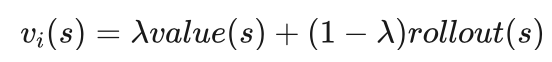
其中0≤λ≤1为加权系数。
为了方便起见，我们假设当前棋局为s，一个可行的落子点为a，在棋局s下在a处落子后得到的棋局用 表示，用 Q(sa) 表示棋局sa 的平均收益，则：
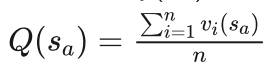
Q(sa) 相当于信心上限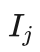 
计算公式中的平均收益 
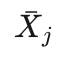。对于还没有模拟过的节点，Q(sa)=value(s) 。
在AlphaGo中定义了一个与模拟次数有关的函数 u(sa) ，并引入了可落子点概率：
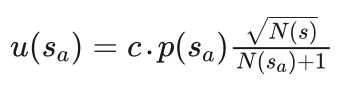
其中 p(sa) 为策略网络给出的在s棋局下在a出行棋的概率，N(s)为棋局s的模拟次数，N(sa) 为棋局 sa 的模拟次数，注意 sa 是在s棋局下在a出行棋后得到的棋局。c为加权系数。
u(sa) 与信心上限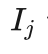 
计算公式中的第二项 
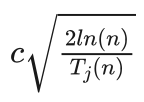对应。所以在蒙特卡洛树搜索的选择阶段，用 Q(sa)+u(sa) 代替信心上限 
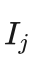，优先选择 Q(sa)+u(sa) 大的子节点。
所以在选择过程中，从搜索树的根节点开始，从上向下每次都优先选择 Q(sa)+u(sa) 大的子节点，直到被选择的节点为叶节点为止，该叶节点被选中，选择过程结束。
小明：明白了，这里将策略网络和估值网络都很好地利用上了。但是艾博士，我有个问题，在前面讲蒙特卡洛树搜索时，选择过程是遇到一个含有未扩展的子节点的节点时，扩展过程结束。这里为什么是被选择的节点为叶节点时结束呢？
艾博士解释说：AlphaGo在这方面做了一点小改进，这与下面将要讲到的扩展方式有关。在AlphaGo中是一次扩展出被选中节点的所有子节点，但只对被选中的节点进行模拟，这是因为即便是没有模拟过的节点，也可以根据策略网络和估值网络的输出计算出 Q(sa)+u(sa) 从而进行选择。这样就可以只对被选中的节点进行模拟，从而提高了效率。
小明：原来是这样，我明白了。
艾博士接着说：如同刚才讲过的，扩展过程就是生成出被选中节点的所有子节点，每个子节点对应一个可能的走步，并通过策略网络、估值网络分别计算出每个子节点的行棋概率和估值。
接下来就是模拟过程，对被选中的节点进行随机模拟。如果模拟结果获胜，则收益为1，模拟结果为获败，则收益为-1。模拟结果和估值网络计算出的收益估值加权平均后作为被选中节点本次模拟的收益 vi(s) 。这里有个需要注意的地方，就是模拟的是被选中的节点，而不是该节点的子节点，这些子节点是否被模拟以及什么时候模拟，需要看后续是否被选中。这也是与之前讲的蒙特卡洛树搜索不一样的地方。
在蒙特卡洛树搜索的模拟过程中，AlphaGo并不是完全随机地行棋模拟，而是按照策略网络给出的每个落子点的概率进行模拟。前面我们说过，随机模拟的次数越多，其结果越可信，为了在一定的时间内获得更多次的模拟，AlphaGo中又设计了一个快速网络，该网络的功能与策略网络完全一样，只是神经网络的结构更简单，虽然牺牲了一些性能，但是速度很快，大概是策略网络的1000倍。
小明：竟然快了这么多啊，为了更多的模拟次数，牺牲一些性能也是值得的。
艾博士：在蒙特卡洛树搜索的回传过程中，对每次模拟得到的结果 vi(s) 要逐层向上回传到其祖先节点，在回传过程中要注意正负号的变化，因为对于一方是正的收益的话，对于另一方就是负的收益。比如图2.16所示的，a是当前棋局，b、c、d是依次产生的后辈节点，经模拟后d获得收益v，该收益依次向上传，由于b和d是同一方产生的节点，所以d的收益要加到b的总收益中，而c、a是d对手方产生的节点，所以要从c、a的总收益中减去v。
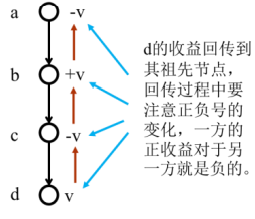
图2.16 回传过程示意图
小明说：原来是这样的，我明白了。
艾博士：除了刚刚讲过的选择过程中的小改进外，在AlphaGo中还有几个小改进。
（1）在蒙特卡洛树搜索中，并不是一直生成新的节点，当达到指定深度后，就不再生成新的子节点了。也就是说，只生成指定深度以内的节点。
（2）规定了一个总模拟次数，当达到该模拟次数后，则蒙特卡洛树搜索结束。选择当前棋局的子节点中被模拟次数最多的节点作为选择的行棋点，而不是收益最高的子节点。
小明：这是为什么呢？为什么不选择收益最高的子节点？
艾博士解释说：主要为了防止由于模拟次数不足造成的虚假高收益。不过按照蒙特卡洛树搜索的选择方法，绝大多数情况下模拟次数最多的节点与收益最高的节点是一致的，个别情况下不一致时，宁愿选择模拟次数最多的节点，这样更加可靠。
小明：听您这么一讲觉得挺有道理的啊。
艾博士：最后我们再把AlphaGo的蒙特卡洛树搜索过程梳理一遍，图2.17给出搜索示意图，这是一个简化图，一些节点并没有画出来。
（1）每个节点记录以下信息：
总收益。总收益包括该节点初次被选中时通过模拟和估值网络获得的加权平均收益，以及在搜索过程中，其后辈节点收益回传得到的收益总和。
行棋概率。从其父节点行棋到该节点的概率值，通过策略网络计算得到。
选中次数。该节点被选中的总次数。
（2）以当前棋局为根节点开始进行蒙特卡洛树搜索。
（3）选择过程如图2（a）所示，从根节点开始从上到下依次选择 最大的子节点，直到被选择的节点为叶节点为止。图中假定先后选择了a、b、c，其中c为最后选定的节点。
（4）扩展过程如图2（b）所示，生成c的所有子节点，并通过策略网络计算出从节点c到每个子节点的概率，通过估值网络计算出c的每个子节点的估值。设置这些子节点的总收益为0，选中次数为0。在AlphaGo中为了不使搜索树过于庞大，限定了一个最大搜索深度，如果被选定的节点已经达到了这个深度，就不再对其做扩展，也就是不再生成其子节点。
（5）模拟过程如图2（c）所示，随机对c进行模拟，根据模拟结果获得收益，获胜为1，获败为-1。计算模拟结果和估值收益的加权平均值作为c的此次模拟的收益v。注意，这里模拟的对象是c，而不是c的子节点。这与一般的蒙特卡洛树搜索有所不同。
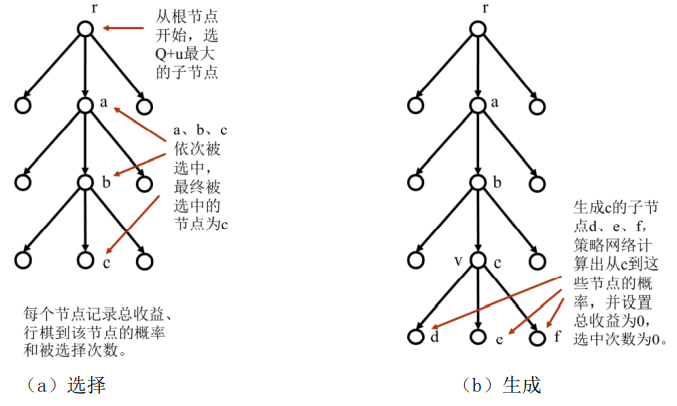
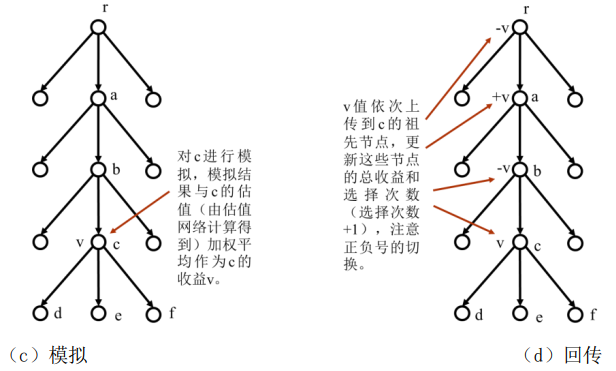
图2.17 AlphaGo的蒙特卡洛树搜索
（6）回传过程如图2（d）所示，将c的收益v回传给c的祖先节点，注意对于一方的收益为v的话，对于另一方的收益就是-v，所以在回传时v的正负号要交替改变，按照回传的正负号将收益v或者-v累加到c的祖先节点中，更新这些节点的总收益，并且对包括c在内的相关节点的选中次数加1。
（7）重复（3）到（6）的过程，直到达到了给定的模拟次数，或者用完了给定的时限。
（8）从根节点的所有子节点中选择一个被选中次数最多的节点，作为本轮的行棋点下棋。等待对手行棋后，再根据对手的行棋情况再次进行蒙特卡洛树搜索，选择自己的行棋点，直到双方分出胜负，对弈结束。
小明读书笔记
AlphaGo的基本框架是蒙特卡洛树搜索，在蒙特卡洛树搜索中引入了两个神经网络——策略网络和估值网络。
策略网络的输入是当前棋局，输出是每个可落子点的行棋概率。该网络通过学习人类棋手的16万盘棋谱得到，采用的是交叉熵损失函数。
估值网络输入是当前棋局，输出是当前棋局的收益估值，取值在正负1之间。同样是通过学习人类的16万盘棋谱得到，采用的是误差的平方损失函数。
此外，AlphaGo还有一个快速网络，功能与策略网络是一样的，只是结构更简单，速度更快，比策略网络大概快1000倍，用于蒙特卡洛树搜索中的模拟过程。
AlphaGo对蒙特卡洛树搜索做了如下改进：
在选择过程中，从根节点开始从上向下每次优先选择 Q(sa)+u(sa) 值大的子节点，该值综合考虑了落子点的概率、估值和模拟次数。
在生成过程中，并不是一直生成新的节点，当达到指定深度后，就不再生成新的子节点了。也就是说，只生成指定深度以内的节点。
规定了一个总模拟次数，当达到该模拟次数后，则蒙特卡洛树搜索结束。选择当前棋局的子节点中被选中次数最多的节点作为选择的行棋点，而不是收益最高的子节点。
未完待续