第二篇 计算机是如何学会下棋的（四）
清华大学计算机系 马少平
第四节：蒙特卡洛树搜索
小明听完艾博士的讲解，赞叹到：看起来α-β剪枝算法的效果还是非常显著的，但是为什么一直没用应用于围棋呢？
艾博士：α-β剪枝算法不仅是在国际象棋上取得了成功，在中国象棋上也取得了成功。前面介绍过的浪潮杯中国象棋人机大战，采用的就是α-β剪枝方法。这种方法也不是没有用到围棋上，只是基本不成功，采用这种方法设计的围棋软件水平很低，别说是专业棋手了，就连普通业余棋手也不能战胜。
小明不解地问：那是为什么呢？
艾博士解答说：很多人对此进行过分析，其中的一个观点是，围棋可能的状态多，比象棋复杂，所以实现的计算机下棋软件水平不行。这种观点是不对的。围棋可能的状态数确实比象棋多，可能的状态数多也确实带来了很大的难度，但这并不是根本原因。前面我们讨论过，α-β剪枝算法严重依赖于对局面评估的准确性，在这方面无论是国际象棋还是中国象棋，都相对容易一些，而且不同高手间对于局面评估的一致性也比较好。也就是说，对于同一个局面究竟是对甲方有利，还是对乙方有利，不同棋手之间看法基本一致，不会有太大的分歧。但是对于围棋来说，局面评估难度就大多了，而且由于不同棋手之间的风格不同，局面评估的一致性也比较差。另外，对于象棋来说，棋子之间的联系不像围棋那么大，可以通过对每个棋子评估实现对整个局面的评估，像前面提到过的，通过对每颗棋子单独评分再求和就可以实现对整个局面的评估。而围棋棋子之间是紧密联系的，单个棋子一定要与其他棋子联系在一起考虑，才有可能体现出它的作用。这些均给围棋局面评估带来很大的难度。另外，脑科学研究也表明，棋手在下象棋时更多的用的是左半脑，而下围棋时则更多的用的是右半脑，而一般认为左半脑负责逻辑思维，右半脑负责形象思维，而计算机处理逻辑思维的能力强于处理形象思维的能力。
小明：还真存在您说的这些问题。
艾博士继续说到：正是由于这样的原因，以前以α-β剪枝算法为基础的围棋程序都没有取得成功。所以如果想提高计算机下围棋的水平，首先要解决围棋的局面评估问题。正是在这一背景下，蒙特卡洛树搜索方法被提了出来。
小明有些疑惑地问到：蒙特卡洛树搜索？
艾博士进一步解释说：这一方法是将传统的蒙特卡洛方法与下棋问题中的搜索树相结合而产生的一种方法。
下面先简单介绍一个蒙特卡洛方法。这个方法是一类基于概率方法的统称，不特指某种具体的方法，最早由冯诺依曼和乌拉姆等人发明，用随机数求解一些计算问题，“蒙特卡洛”这个名称来源于摩纳哥的一个赌场的名字。
为了对这一方法有所体会，我们举一个用蒙特卡洛方法计算π值的例子。
艾博士问小明：小明，你知道π如何计算吗？
小明回答说：有很多种方法可以计算π，最早祖冲之就采用割圆术计算π值，得出了π值介于3.1415926和3.1415927之间的结论。
艾博士称赞说：小明你记得很准确，在当时没有任何计算工具的情况下，这是一项很了不起的成就。如果只给你一张带格子的稿纸和一根针，你能求出π值吗？
图2.7 蒲丰投针
小明摸着自己的小脑瓜说：只有一张稿纸和一根针，这怎么能求出π值呢？
艾博士说：法国数学家蒲丰就给出了一种称作“蒲丰投针”的计算π值的方法，其实就是最早的蒙特卡洛方法的运用。
小明迫不及待地说；这太神奇了，艾博士你快讲讲。
艾博士：如图2.8所示，假设有一张放在桌子上带格子的稿纸，随机向纸上扔一根针，那么针与格子之间会呈现出不同的状态，有时候针会与格子相交，有时候针会落在两条线之间。
图2.8 蒲丰投针示意图
为了方便计算，我们可以将蒲丰投针问题简化为图2.9所示的情况。图中左边是针与格子相交的情况，假设针的长度为l，格子的宽度为d，针与格子底线的夹角为α，针的中间位置到格子底线的距离为x。图中右边是一种针刚好与底线相交的边缘情况，针如果再向上一点，就不会与格子底线相交了。所以这时的 就是针与底线相交的最大值。当 x<=x0 时，针与底线是相交的，否则针就不会与底线相交。
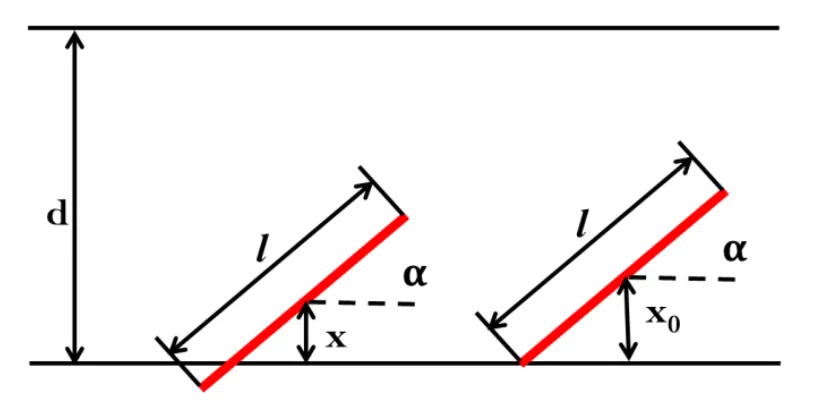
图2.9 蒲丰投针计算示意图
按照三角函数公式我们有：
所以针与底线相交的条件就是：
夹角α的可能变化范围应该是[0,2π]，对于针来说如果我们不区分针头和针尾的话，夹角α处于[0，π]和[π，2π]是一样的，所以为了简化起见，我们只考虑[0，π]这一变化区间。同理对于针的中间位置是处于格子的上半段还是下半段也是一样的，因为如果处于下半段就看是否与底线相交，如果处于上半段就看是否与顶线相交，所以我们也只考虑是否与底线相交这种情况。这样的话，x的取值范围是[0,d/2]，α的取值范围是[0,π]。
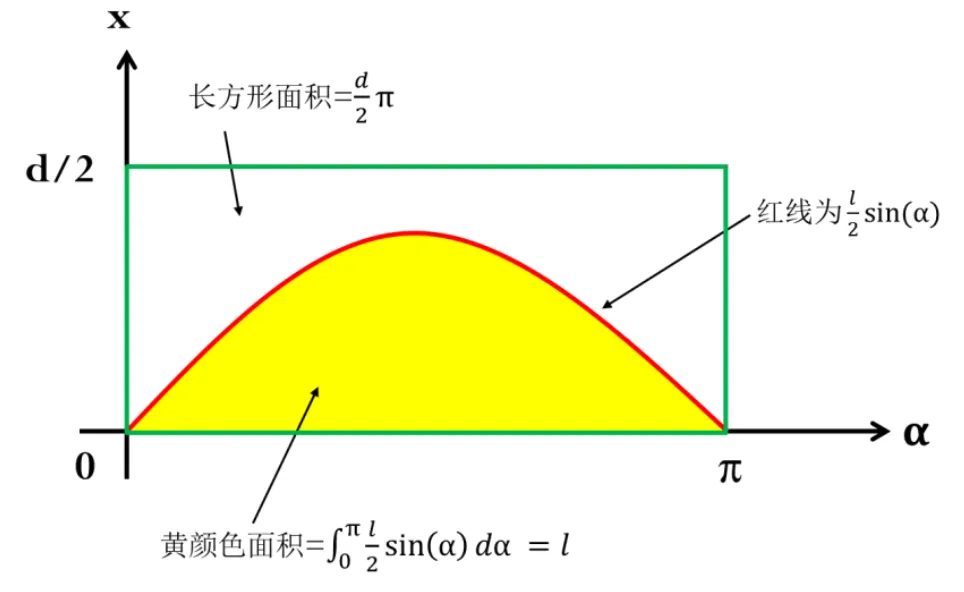
图2.10 蒲丰投针计算π值示意图
一旦确定了α和x之后，针的位置就确定了。如图2.10所示，绿色长方形内任何一点（α，x）就确定了一次投针的位置，按照针与底线相交的条件，黄色区域代表针与底线相交，绿色长方形内的白色区域，代表针没有与底线相交。所以黄色区域的面积除以绿色长方形的面积，就是针与底线相交的概率p( 相交 )。
按照面积的计算公式，绿色长方形的面积为：
艾博士问小明：这里用到了定积分，你还会计算吗？
小明回答说：这个定积分应该不难，我会计算。
艾博士：好的，如果忘记了回去自己复习一下。
艾博士接着讲到：另一方面，如果我们投掷了n次针，其中有m次针是与底线相交的，那么针与底线相交的概率就是：
只要投掷针的次数足够多，就可以求得一个一定精度的π值。
小明看着艾博士的推导赞叹到：竟然还可以这样求解π值，可真是神奇。
艾博士说：这种方法就是蒙特卡洛方法，通过将一个计算问题转化为概率问题后，利用随机性，通过求解概率的方法求解原始问题的解。小明，你回去后可以编写一个程序，利用随机数发生器随机产生一些满足要求的x和α，通过模拟投针的办法计算π值。
小明说：好的，我回去一定试试这个神奇的方法。那么这种方法如何应用到围棋中呢？
艾博士：小明，围棋程序遇到的最大问题是什么？
小明回答说：刚才您讲过了，主要是对棋局的估值问题。
艾博士：对啊，既然这个棋局估值问题不容易解决，我们是否也可以利用随机模拟的办法评价一个棋局呢？比如说，对于给定的围棋棋局我们让计算机随机地交替行白棋和黑棋，直到一局棋结束，判定出胜负。这样就得到了一次模拟结果。当然一次模拟结果不说明任何问题，计算机的优势就是速度快，可以在短时间内几万、几十万次地进行模拟。如果模拟的次数足够多，我们就可以相信这个模拟结果。如果大量的模拟结果显示黑棋获胜概率大，那么就有理由认为当前的棋局对黑方有利，否则就认为对白方有利。
小明说：竟然这么简单啊，棋局估值问题解决了，是不是就可以写出高水平的围棋程序了？
艾博士：还没有这么简单，这只是一个思路，但是确实给实现高水平围棋程序指明了方向。
小明问道：那么还存在什么问题呢？
艾博士提示说：小明你想想，下棋是甲乙双方一步一步轮流进行的，我们在模拟过程中是否需要考虑这个因素呢？就像前面我们讲过的极小-极大模型中说过的一样，甲方希望走对自己最有利的棋，乙方也希望走对自己最有利的棋，双方是一个对抗的过程。所以在模拟过程中应该考虑到这种一人一步的对抗性问题，将搜索树考虑进来。正是在这样的思想指导下，才提出了我们马上要讲的蒙特卡洛树搜索方法，在随机模拟的过程中，将一人一步的搜索过程考虑进来。
小明：我明白了，确实需要考虑这个问题，否则就是只想着自己怎么行棋，完全不考虑对方可能的行棋方法，这样不可能达到高水平的。
图2.11 蒙特卡洛树搜索示意图
艾博士：为此有研究者将蒙特卡洛方法与下棋问题的搜索树相结合，提出了蒙特卡洛树搜索方法。
蒙特卡洛树搜索方法如图2.11所示，共包括4个过程：
（1）选择过程：如图2.11第一个图所示，从根节点r出发，按照某种原则自上而下地选择节点，直到第一次遇到一个节点，该节点还存在未生成的子节点为止。如图所示，从根节点r开始，从r的3个子节点中按照某种原则选择一个节点，假设选择了节点a。接下来又从a的子节点中选择节点，假设选择了b。这时发现b还存在子节点没有生成，则选择过程结束，节点b被选中；
（2）扩展过程：如图2.11第二个图所示，生成出被选中节点的一个子节点，并添加到搜索树中。由于在上一步选中的节点为b，所以生成出b的一个子节点c，然后将节点c添加到搜索树中；
（3）模拟过程：如图2.11第三个图所示，对新生成的节点c进行随机模拟，即黑白轮流随机行棋，直到分出胜负为止。然后根据模拟的胜负结果计算节点c的收益△。
（4）回传过程：如图2.11第四个图所示，将收益△向节点c的祖先进行传递。因为对节点c的一次模拟也相当于对c的祖先节点b、a、r各进行了一次模拟，所以要将对节点c的模拟结果回传到c的祖先节点b、a、r。
在上述4个过程中，第二个扩展过程比较简单，直接生成一个被选中节点的子节点，并添加到搜索树上就可以了。第三个模拟过程也比较简单，就是随机地轮流选择黑白棋，按规则行棋就可以了，直到能分出胜负为止。当然具体如何随机行棋、如何计算胜负等与具体的围棋规则有关，我们就不具体讨论了。第四个回传过程与具体的收益表示方法有关，我们留待后面结合具体例子再详细讲解，下面我们重点介绍第一个过程——选择过程。
选择过程就是选择哪个节点进行模拟，这里的模拟不一定是直接对该节点做随机模拟，也可能是通过对其后辈节点的模拟达到对该节点模拟的目的。因为就如同在回传过程中所说的那样，后辈节点的一次模拟，也相当于对其祖先节点做了一次模拟。所以在选择过程中，如果一个节点的子节点全部生成完了，则要继续从其子节点中进行选择，直到发现某个节点，它还有未生成的子节点为止。
小明不太明白地问：为什么要进行选择呢？或者说选择的目的是什么呢？
艾博士：选择的目的就要在有限的时间内对重点节点进行模拟，以便挑选出最好的行棋走步。我举个例子说明吧，假设你是班级体委，学校要举行篮球比赛，你要挑选上场队员。有些同学你比较了解，因为你知道这些同学以前打球比较好，有些同学你不太了解，不知道水平如何。为了确定上场队员，你计划打几场热身赛对同学们进行考察。考察过程中，对于以前你认为打球好的同学，你可能让他们上场打打试试，看是否还继续保持高水平。对于你不太了解的同学，你也可能让他们上场试试，以便了解他们的水平究竟如何。
小明：如果我是班级体委确实要这么做，以便挑选出真正有实力的队员。
艾博士：所以，这里利用了两个原则：
（1）对不充分了解的同学的考察；
（2）对以往水平比较高同学的确认。
选择哪些节点进行模拟就如同在热身赛中考察队员，也遵循这两个原则。在蒙特卡洛树搜索的过程中，根据到目前为止的模拟结果，搜索树上的每个节点都获得了一定的模拟次数和一个收益值，模拟次数可能有多有少，收益值也有大有小。收益值大的节点就相当于以往打球水平比较高的同学，这些节点是真的收益值高呢？还是因为模拟的不够充分暂时体现出虚假的高分呢？需要进一步模拟考察。而对于那些模拟次数比较少的节点，相当于不充分了解的同学，由于模拟的次数比较少，无论收益值高低，都应该优先选择以便进一步模拟，了解其真实情况。
在这样的原则下，选择节点时应该要同时考虑到目前为止节点的收益值和模拟次数，比如对于某个节点x，如果它的收益值又高、模拟次数又少，这样的节点肯定要优先选择，以便确认它的收益值的真实性。如果它的收益值很低、模拟次数又多，说明这个低收益值已经比较可靠了，没有必要再进一步模拟了。所以我们可以得出结论：节点被选择的可能性与其收益值正相关，而与其模拟次数负相关，可以将收益值和模拟次数综合在一起确定选择哪个节点。
小明：那么具体如何选择呢？
艾博士：类似的问题早就有人研究过，我们可以借用过来。比如多臂老虎机模型就是求解此类问题的一种模型。
小明：多臂老虎机？这是个什么模型呢？还与赌博有关？
艾博士：很多概率问题的研究都与赌博有关，我们正在介绍的蒙特卡洛树搜索不也是因摩纳哥的一个赌城而得名吗？赌博不能粘，但是相关的研究成果我们可以利用求解我们的问题，为人类服务。
图2.12多臂老虎机示意图
多臂老虎机是一个具有多个拉杆的赌博机，投入一个筹码之后，可以选择拉动一个拉杆，每个拉杆的中奖概率不一样。多臂老虎机问题就是在有限次行动下，通过选择不同的拉杆，以获得最大的收益。
小明：这个多臂老虎机与蒙特卡洛树搜索中的选择过程具有什么关系呢？
艾博士：选择哪个节点进行模拟，就相当于选择拉动多臂老虎机的哪个拉杆，而模拟得到的收益，则相当于拉动拉杆后获得的收益。
小明：这么一对比就将两个看似无关的问题对应起来了。
艾博士：经过学者们的研究，对于多臂老虎机问题，提出了一种称作信心上限（UCB：Upper Confidence Bound）的算法。
该算法的基本思想是，先每个拉杆拉动一次，记录每个拉杆的收益和被拉动次数，此时拉动次数都是1。按后按照下式计算拉杆j的信息上限值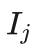 
：
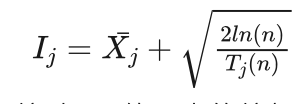
信心上限算法就是每次选择拉动 值最大的拉杆。其中 表示第j个拉杆到目前为止的平均收益，n是所有拉杆被拉动的总次数，ln(n)是取对数，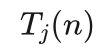 
是总拉动次数为n时，第j个拉杆被拉动的次数。重复以上过程直到达到拉杆被拉动的总次数结束。
上述信心上限方法可以推广到蒙特卡洛树搜索过程的选择过程，也就是从上向下一层层选择节点时，按照信心上限方法，选择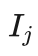 
值最大的子节点，直到某个含有未被生成子节点的节点为止。在具体使用的过程中，一般会增加一个调节系数，以方便调节收益和模拟次数间的权重，如下式所示：
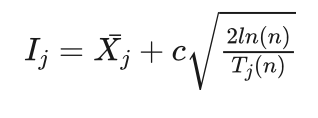
小明：我明白了可以用信心上限方法选择模拟节点。
艾博士：下面我们通过一个具体例子说一下蒙特卡洛树搜索的具体过程，同时也通过这个例子说明如何实现收益的回传过程。为此我们先给出记录收益和模拟次数的方法。对于搜索树中的每个节点，我们用m/n记录该节点的获胜次数m和模拟次数n，收益用胜率表示，即m/n。注意这里的“获胜”均是从节点本方考虑的，也就是这个节点是由甲方走成的，则获胜是指甲方获胜，如果这个节点是由乙方走成的，则获胜指乙方获胜。比如在图2.11中最后一个图中，假设对节点c的模拟结果是获胜，则c的获胜数加1，同时向上传递该结果，由于b是对方走成的节点，我方获胜就是对方失败，所以b的获胜次数不增加。模拟收益再向上传到节点a，a是我方走成的节点，c获胜也相当于a获胜，所以a的获胜数也加1。同样节点r是对方走成的节点，所以r的获胜次数也不增加。
小明：由于搜索树是双方轮流行棋而形成的，所以获胜次数向上传递也是每次相隔一个节点增加的。
艾博士说：小明说的是对的，回传过程正是这样进行的。不过如何回传与我们选用的表示方法是有关的，如果采用其他的表示方法可能就会有所变化。比如说如果获胜我们用1表示，失败用-1表示，则回传时就可能是加1、减1交替地进行。
小明：明白了，原来回传方法还与如何表示有关。
艾博士：所以如果看其他的参考资料的话，一定要先弄清楚具体的表示方法。
艾博士：请看图2.13，我们用这个具体的例子再说明一下蒙特卡洛树的搜索过程。为了简单起见，在计算信心上限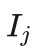 
时，我们假定收益 
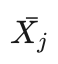为胜率，并假定调节参数c=0，也就是说假定信心上限 
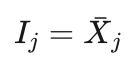。当然这只是为了举例方便计算才这样假设的，实际使用时不会这样。
图2.13（a）是当前的搜索树，从节点r开始进行选择，节点r的三个子节点中，a的信心上限值最大为2/3 ，所以选择节点a。假定a没有其他未生成的子节点了，所以继续从a的两个子节点中选择，节点b的信心上限值最大为 1/2 ，同样假定b也没有其他未生成的子节点了，继续从b的两个子节点中进行选择，节点c的信心上限值最大为 1/1 ，而且由于c存在未生成的子节点，所以选择过程结束，节点c被选中。
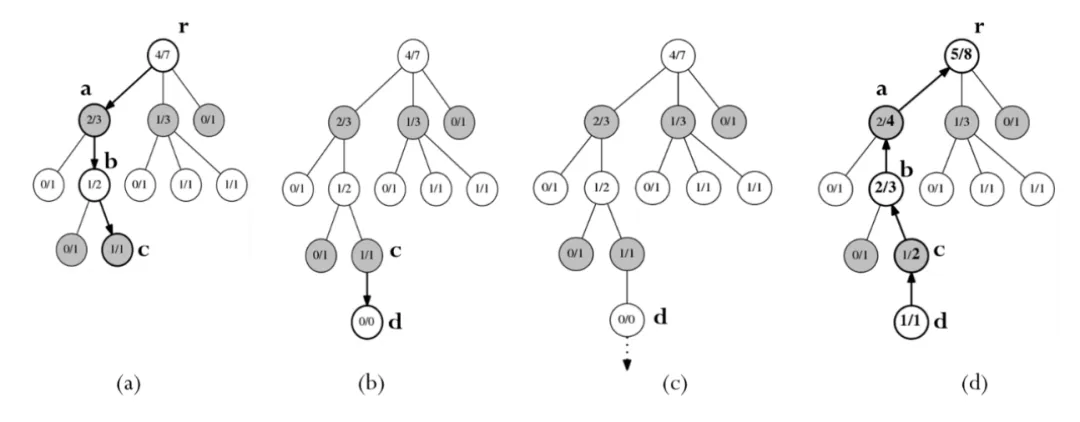
图2.13 蒙特卡洛树搜索举例
进入扩展过程，如图2.13（b）所示，节点d被生成并添加到搜索树中成为节点c的子节点。扩展过程结束。
接下来进入模拟过程，如图2.13（c）所示，对节点d进行随机模拟，黑白双方随机选择行棋点，直到决出胜负。假定模拟结果是胜利，也就是说节点d经模拟后获得了一次胜利。模拟过程结束。
最后是回传过程，首先记录节点d的模拟情况为1/1，表示d被模拟了一次，获胜一次。向上传递。节点c之前的模拟结果是1/1，这次由于d被模拟一次，所以相当于c也被模拟了一次，但是从c的角度来说，这次模拟是失败。所以c的模拟次数增加一次，但获胜次数保持不变，更新c的模拟结果为1/2。继续回传到b，b之前的模拟结果为1/2，这次模拟次数和获胜次数均被加1，所以更新b的模拟结果为2/3。再回传到节点a，该节点只增加模拟次数1次，不改变获胜次数，更新a的模拟结果为2/4。最后再回传到根节点r，该节点获胜次数和模拟次数均增加1次，所以模拟结果为5/8。
至此完成了一轮蒙特卡洛树搜索，反复该过程，直到达到一定的模拟次数或者规定的时间到，结束蒙特卡洛树搜索。
小明：蒙特卡洛树搜索结束之后如何选择最佳走步呢？
艾博士：搜索结束后，根据根节点r的子节点的胜率，选择胜率最大的子节点作为我方的行棋点。因为按照刚刚结束的蒙特卡洛树搜索结果，这样可以获得最大收益。
小明仔细看着图2.13的示例，陷入沉思中，过了一些时候才问艾博士：在选择过程中，一直都是选择信心上限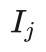 
的最大值，哪里体现出了像极小-极大过程中的我方取最大、对方取最小的思想呢？按理说到对方节点时，应该选取胜率小的才对啊。
艾博士：小明提出了一个很好的问题。这也跟我们的表示方法有关。还记得刚才讲解如何标记模拟结果时，我们记录的是从节点方角度考虑的获胜次数。也就是我方走成的节点记录的是我方的获胜次数，对方走成的节点记录的是对方的获胜次数。所以当我方选择时选择的是信心上限最大的节点，如果只考虑胜率的话，就相当于选择胜率最大的节点。而当对方选择时，虽然也是选择信心上限最大的节点，但是其中与胜率有关的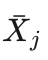 
用的是对方的胜率，所以选的是对对方最有利而对我方最不利的节点。所以与极小-极大模型也是一致的，之所以极小-极大模型中我方选最大、对方选最小，是因为表示棋局的数字都是从我方角度考虑的，而在这里胜率是从各自角度考虑的。这样做的好处是，在选择过程中可以不考虑我方和对方，都统一选择最大就可以了，比较方便统一。
小明想了想说：确实是这么回事，这样感觉更简单了。
小明读书笔记
蒙特卡洛方法是一类基于概率方法的统称，最早由冯诺依曼和乌拉姆等人提出，用随机数求解一些计算问题。“蒙特卡洛”这个名称来源于摩纳哥的一个赌场的名字。为了解决围棋局势不容易判断的问题，将蒙特卡洛方法引入进来，通过随机模拟的方法判断棋局的局势。结合围棋下棋双方轮流走子的特点，提出了蒙特卡洛树搜索方法。
蒙特卡洛树搜索方法包含4个过程：
选择过程：这是蒙特卡洛树搜索的重点，借助于多臂老虎机模型的已有研究成果，从搜索树的根节点开始，从上到下依次选择信息上限最大的节点，直到遇到第一个含有子节点未被扩展的节点。
信心上限的计算公式为：
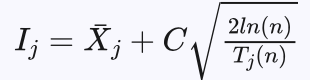
其中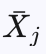
为第j个子节点的平均收益，n为父节点的模拟次数，
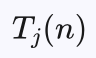为第j个子节点的模拟次数，C为调节系数。
多臂老虎机模型综合体现了以下两个原则：
对收益好的节点的确认；
对不充分了解的节点的考察。
扩展过程：为被选择的节点生成一个新的子节点，也就是一种可行的走步之后得到的棋局。
模拟过程：从新的子节点开始进行随机模拟，直到分出胜负。
回传过程：将模拟结果向上回传到新节点的祖先各节点，回传时要注意对弈双方各自的立场。
当蒙特卡洛树搜索结束时，从根节点的各个子节点中选取平均收益最大的子节点作为最佳走步。
需要注意的是，每次轮到机器行棋时，都要以当前棋局作为根节点进行一次蒙特卡洛树搜索，以便找出当前棋局下计算机应该选择的走步。
未完待续