第四篇 如何用随机算法求解组合优化问题(三)
清华大学计算机系 马少平
第三节:局部搜索算法存在的问题
小明:请问艾博士,局部搜索算法存在哪些问题呢?
艾博士:局部搜索算法主要的问题是不能保证找到全局最优解,当待求解问题具有多个极值点时,该问题更加突出。下面我们具体分析一下都与哪些具体的因素有关。
1、局部最优问题
为了更形象地说明问题,下面我们假设求问题的最大值,以爬山过程为例做讲解,这样更容易理解。
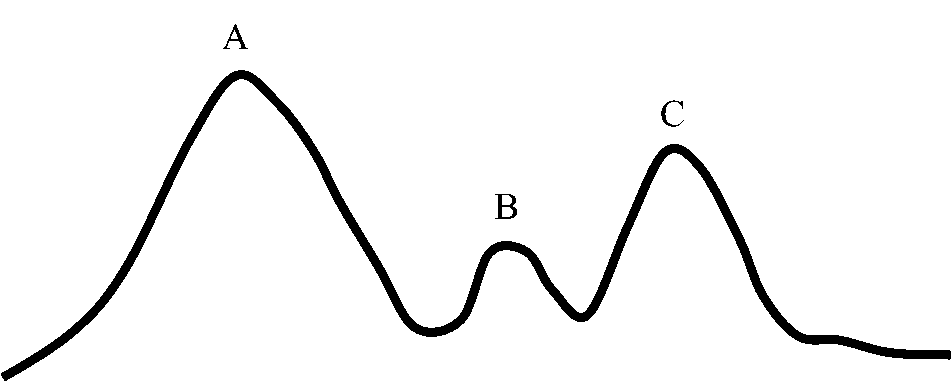
图4.6 局部最优问题
如图4.6所示的山峰,具有A、B、C多个局部最优值,只有A是我们希望的全局最优解。如果用局部搜索算法进行求解,则可能到达任何一个局部最优解后,由于满足算法的结束条件导致算法结束。这时可能是A、B、C的任何一点,因此存在找不到全局最优解的可能性。这就是局部最优问题。
小明:是否有解决局部最优解的办法呢?
艾博士:我们可以给算法增加一些随机因素。在局部搜索算法中,每次接受邻域内的一个最好的结果,也正是由于这种“贪婪”的选择,才会导致在某个局部最优点而非全局最优点结束。一种解决办法是,在局部搜索算法中,我们按概率接受一些好解,也按概率接受一些差解,越好的解被接受的概率越大,越差的解被接受的概率越小。这样在算法搜索过程中,就有一定的概率逃离局部最优点,而奔向全局最优点。也就是说,从邻域中随机选择一个解,如果该解的指标函数好于当前已知的最好解,则以大概率接受该解,否则就以小概率接受,而不是只是一味地只接受好解,拒绝差解。也就是所谓的“迂回,是为了更好地前进”。
小明:那么如何计算接受概率呢?
艾博士:当求指标函数的最大值时,可以按照下式计算接受概率:
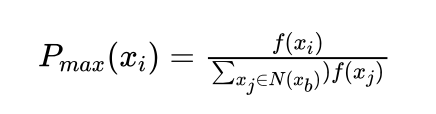
其中xb 为当前获得的最好解, N(xb) 为xb 的邻域,xi 为邻域中的一个解,Pmax(xi) 为 xi 被接受的概率,指标函数值 f(xi) 越大的解,其被接受的概率也越大。
小明:如果想求最小解怎么办呢?
艾博士:求最小解时,应该刚好反过来,f(xi) 越小的解,其被接受的概率越大,而f(xi) 越大的解,其被接受的概率越小。一种简单的办法可以这样计算:
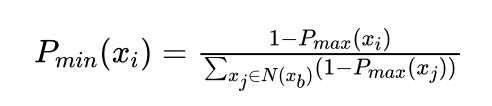
也可以设立一个比较大的常数M>0,通过求M-f(xi) 的最大值求解 f(xi) 的最小值。
小明:这个方法挺方便的,把一个求最小值问题转化为了求最大值问题。有了接受概率,如何根据接受概率判断是否接受了呢?
艾博士:小明这个问题问得好!我们可以通过随机数发生器模拟按概率接受这一随机现象。
小明:什么是随机数发生器?怎么用来模拟随机现象呢?
艾博士:一般的程序设计语言中都会有一个随机数发生器函数,利用该函数可以产生一个[0,1]之间的均匀分布的随机数。设random(0,1)为随机数发生器,每调用一次就产生一个[0,1]之间的随机数。设被接受的概率为P,是[0,1]之间的一个小数。为了方便说明,我们假设P=0.6。
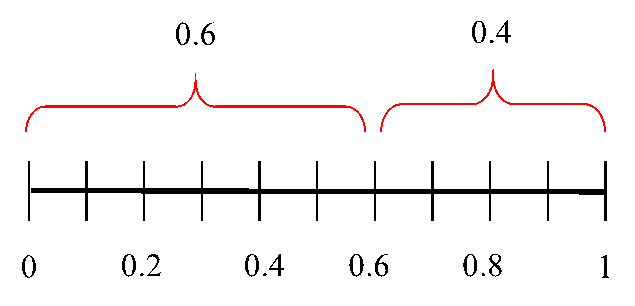
图4.7 按概率P接受示意图
如图4.7所示,如果当前解被接受的概率为0.6,那么该解是否被接受呢?这时就要看random(0,1)的值了。由于random(0,1)是在[0,1]之间均匀分布的,所以其产生的随机数落入[0,0.6]区间的概率为0.6,落入[0.6,1]区间的概率为0.4。现在当前解被接受的概率为0.6,如果random(0,1)产生的随机数落入[0,0.6]区间,也就是该随机数小于0.6时,当前解就被接受,否则就不被接受。一般情况下,当random(0,1)<p时,当前解就被接受。这就是利用随机数函数模拟按照概率接受一个差解的方法。
小明:原来随机数函数还可以这么用,又长见识了。
艾博士:这样我们就得到了一个改进的局部搜索算法,该方法按照概率接受一个新解:
局部搜索算法1(Local Search 1)
1、随机的选择一个初始的可能解 x0∈D ,xb=x0 , P=N(xb) ;
2、对于所有的x∈P计算指标函数f(x),并计算x被接受的概率P(x)
3、如果不满足结束条件,则
4、Begin
5、从P中随机选择一个解xn
6、如果 random(0,1)<p(xn) 则接受 xn ,xb = xn,p=N(xb) ,转2
7、否则将 xn 从P中删除,如果P为空则转9,否则转5
8、End
9、输出计算结果
10、结束
2、步长问题
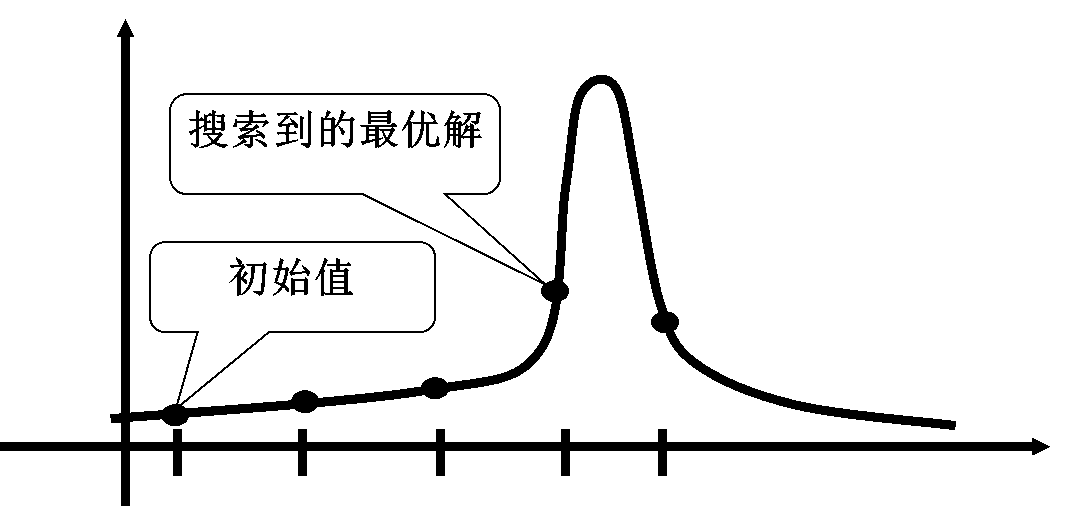
图4.8 步长问题示意图
艾博士:局部搜索算法存在的第二个问题是步长问题。
小明:什么是步长?步长问题又是指什么问题?
艾博士:简单地说,步长就相当于爬山法中“拐杖”的长度,相当于探寻到的局部信息的范围。如图4.8所示,如果山峰比较尖,而步长比较大的话,就可能出现越过山峰最高点的情况,找到了一个错误的最高峰。
小明:哪有那么大的步子啊?另外我们变小步长不就可以了?
艾博士:这只是一个比喻。因为实际问题中,山峰的宽度我们往往并不知道有多大,也正因为如此,我们也往往不知道多大的步长是个合适的步长。如果步长太小的话,移动的太慢,严重影响求解效率。如果步长过大的话,则可能出现刚刚说过的错过最高峰的情况。小明,你想想可以怎么解决这个问题呢?
小明思考了一会说:是不是可以这样解决?开始步长可以大一点,然后再改变步长,逐渐减少步长。
艾博士:这是一种很好的解决办法,这就是“变步长”方法。图4.9给出了这种变步长方法的示意图。
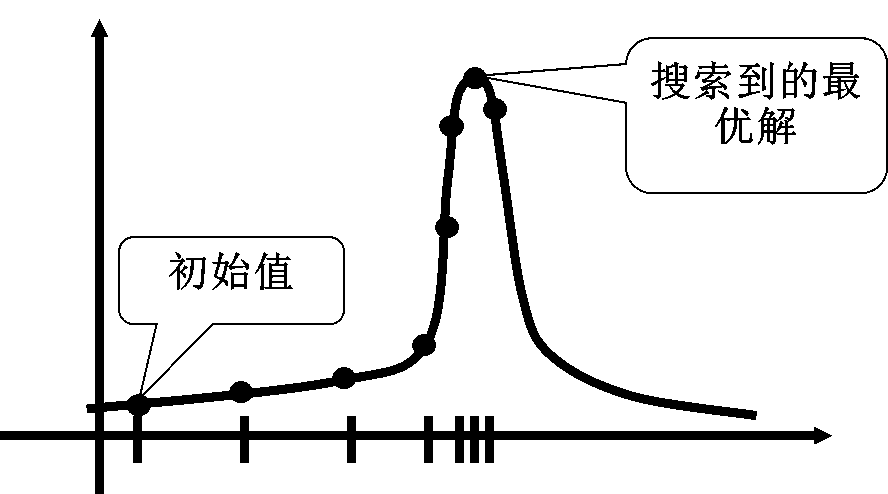
图4.9 变步长方法示意图
小明:但是怎么实现变步长呢?应该如何变才合适呢?
艾博士:是的,这是一个问题。变步长很容易想到,但是问题是怎么变才合适,这是一个一个需要思考的问题。
下面我们给出变步长的局部搜索算法,该算法每次获得一个新解后改变一次步长,在新步长下计算解的邻域。
局部搜索算法2(Local Search 2)
1、随机的选择一个初始的可能解 x0∈D,xb=x0 ,按步长计算邻域P=N(xb) ;
2、如果不满足结束条件,则
3,Begin
4、选择P的一个子集P',xn 为P'中的最优解
5、如果 f(xn)<f(xb) ,则xb =xn ,改变步长计算邻域 P=N(xb) ,转2;
6、否则P = P–P',转2。
7、End
8、输出计算结果
9、结束
3、起始点问题
艾博士:当具有多个山峰时,局部搜索算法能得到什么样的结果,取决于起始点的位置,开始位置不同,得到的结果就可能不同。如图4.10所示,如果起点位置在A处,就可以找到全局最优值,如果起点位置在B处,就只能找到局部最优值。
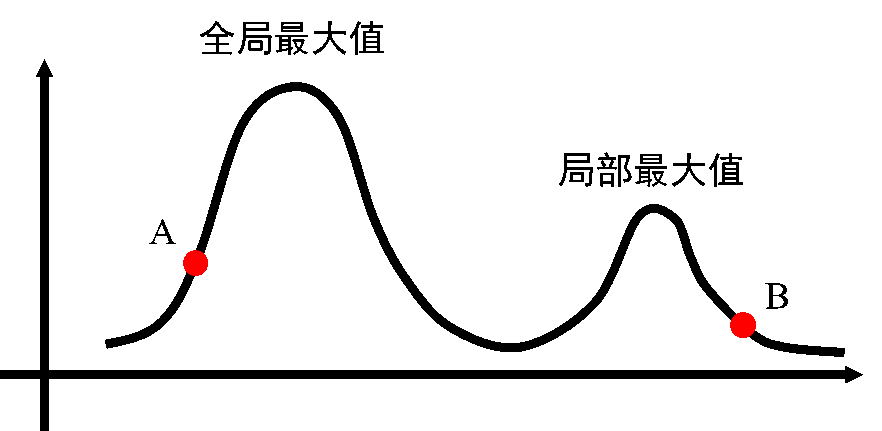
图4.10 起始点问题示意图
这个问题解决起来相对比较简单,可以通过多次运行局部搜索算法的方法来解决。每次随机设置起始位置,然后从多个不同起始位置的结果中找一个最好的结果。当然这样也不能保证找到的一定是全局最优解,但是如果运行的次数足够多,则有较大的概率找到全局最优解。
事实上,在前面的百万皇后例子中,就是采用的这种多次运行的方法,只是皇后问题事先知道最优值是多少,一旦找到了最优解就可以结束。而一般的组合优化问题就没有这么幸运了,我们并不知道什么时候算法结束才是合适的。
下面给出随机设置多个起始点的局部搜索算法,与基本的局部搜索算法相比,在最外层增加了一个循环,控制算法的运行总次数,并从多次运行结果中,选取一个最好的结果作为算法的输出。
局部搜索算法3(Local Search 3)
1、k=0;
2、随机的选择一个初始的可能解 x0∈D ,xb=x0 ,P=N(xb) ;N(xb) 为求 xb 的邻域
3、如果不满足结束条件,则
4、Begin
5、选择P的一个子集P',xn 为P'中的最优解
6、如果 f(xn)<f(xb) ,则 xb=xn ,P=N(xb) ,转3;f(x)为指标函数。
7、否则P = P–P',转3。
8、End
9、k = k+1
10、如果k达到了指定的次数,则从k个结果中选择一个最好的结果输出,否则转(2)
11、输出计算结果
12、结束
艾博士总结说:以上就是局部搜索算法存在的几个问题,以及解决这些问题的方法。这些方法还只是一些原则性的方法,还需要进一步的具体实现。下一节将要介绍的模拟退火算法就属于将(1)和(2)两种方法结合起来实现的一个局部搜索算法,如果再加上算法的多次运行,就实现了三种改进方法的融合。
小明读书笔记
局部搜索算法存在局部最优问题、步长问题和起始点问题等3个问题,从而使得局部搜索算法不能保证求解到全局最优解。为了提高求解全局最优解的概率,针对不同的问题可以寻求不同的改进思路。
针对局部最优值问题,解决思路是以一定的概率接受新解,越好的解接受概率越大,越差的解接受概率越小,核心是以一定概率接受差解,增加算法跳出局部最优解的可能。
针对步长问题,解决思路就是实现变步长,在求解效率和解的质量之间建立平衡。
针对起始点问题,解决思路是随机设立多个起始点,通过多次运行算法解决。
未完待续

