第四篇 如何用随机算法求解组合优化问题（四）
清华大学计算机系 马少平
第四节：退火过程及分析
小明：刚才您提到模拟退火算法，听起来这个算法怎么还和物理有关呢？
艾博士：模拟退火算法是为了解决局部搜索算法存在的问题,受物理中金属退火现象的启发而提出的一个随机算法。作为求解复杂组合优化问题的一种有效的方法，模拟退化算法已经在许多工程和科学领域得到广泛的应用。
小明：原来模拟退化算法名称来源于此。
1、退火现象
艾博士：我们先回顾一下物理中的退火现象。小明，我们先做个实验吧。这里有一根细钢丝，你可以用这根钢丝做一个弹簧吗？
图4.11 弹簧示意图
小明找来一根圆筷子，努力地将钢丝缠在筷子上，做成弹簧的形状。但是由于钢丝具有很好的弹性，好不容易缠好的钢丝，一松手就立即回复了原状，无论如何也做不好一个弹簧。
看着小明满头大汗、垂头丧气的样子，艾博士说：由于钢丝具有弹性，这样是不可能做好一个弹簧的。这样吧，我们将先钢丝加热一下，再将它放置在房间里，让它慢慢冷却，再看情况会发生什么变化。
艾博士点燃了煤气灶，用一把钳子夹着钢丝，在煤气灶上对钢丝进行加热，边加热边不停地移动钢丝，让钢丝尽可能受热均匀。不一会的功夫，钢丝就被烧的通红。
艾博士对小明说：加热的钢丝需要慢慢冷却，今天时间也不早了，我们就先讲到这里，明天我们再看冷却后的钢丝会发生什么变化。
小明一晚上都在想着实验的事，第二天一早就来到艾博士家，想尽快知道结果。
艾博士对小明说：你再试试看，这次是否容易一些了？
小明拿着处理过的钢丝，再次在筷子上缠绕起来，发现原来硬邦邦、具有弹性的钢丝，变得非常“温顺”起来，很容易就将钢丝做成了一个弹簧状的样子。
小明：这次容易多了，但是这样做成的“弹簧”没有任何弹性啊，只是形状象个弹簧样，根本起不到弹簧的作用。
艾博士解释说：是的，这样做成的不还能叫弹簧，还需要再处理一下。
说完，艾博士又用钳子夹着做好的弹簧在煤气炉上加热起来。艾博士让小明准备好一盆冷水，等弹簧被烧的慢慢变红之后，艾博士迅速地将火红的弹簧扔到冷水中，随着“吱吱”的响声，盆中冒起来“白烟”。不一会功夫，弹簧就被冷却了。
艾博士拿起冷却后的弹簧对小明说：你再试试看，是不是有弹性了？
小明拿起弹簧用手拉伸了一下说：好神奇啊，这次果然有弹性了。这是为什么呢？
艾博士解释说：第一次我们将钢丝加热后，让其慢慢地冷却，这叫“退火”。经退火处理的钢丝，其内能处于一种最低状态，这时原来的钢丝就变的很柔软，失去了弹性。第二次我们将做好的弹簧再次加热，将其放入冷水中使其快速地降温，这叫“淬火”。经淬火处理后的弹簧，其内能处于一种高能状态，就又使得弹簧恢复了弹性。
小明：原来是这样啊，很有意思的现象。
艾博士：模拟退火算法就是利用退火的这种现象，将组合优化问题与退火现象对应起来，用算法模拟退火过程，当内能处于最低状态时，刚好对应组合优化问题的最优解。小明我们先对退火过程做一个详细的分析，了解退火过程为什么会使得金属处于最低内能状态，然后再介绍如何利用退火现象求解组合优化问题。
2、退火过程分析
艾博士：这部分内容是一些基本的理论分析，也是将退火过程通过模拟的方法应用于求解组合优化问题的理论依据，会涉及到不少的公式推导，如果对理论推导不感兴趣的话，可以跳过这部分内容。
小明：您还是讲解一下吧，我希望了解为什么模拟退火算法可以求解组合优化问题，而不只是知道算法的具体实现过程。
艾博士：好的，我们就详细讲解一下。在具体讲解之前，我们先介绍一个奇怪的杯子。假设有图4.12所示的怪杯子。该杯子杯壁上有很多的小凹槽，杯底部也有几个一样的小凹槽。这个杯子可以帮助我们理解退火现象。
图4.12 奇怪的杯子
艾博士的话一下就抓住了小明的好奇心：这个奇怪的杯子跟退火现象有什么关系呢？
艾博士：我们先大概介绍一下退火过程。金属的退火过程是一种物理现象，属于热力学和统计物理学的研究范畴。当对一个金属进行加热时，粒子的热运动不断增加，随着温度的不断上升，粒子逐渐脱离开其平衡位置，变得越来越自由，直到达到金属的溶解温度，粒子排列从原来的有序状态变为完全的无序状态。这就是金属的溶解过程。退火过程与溶解过程刚好相反。随着温度的下降，粒子的热运动逐渐减弱，粒子逐渐停留在不同的状态，其排列也从无序向有序方向发展，直至到温度很低时，粒子重新以一定的结构排列。粒子不同的排列结构，对应着不同的内能水平。如果退火过程是缓慢进行的，也就是说，温度的下降如果非常缓慢的话，使得在每个温度下粒子的排列都达到一种平衡状态，则当温度趋于绝对0度时，系统的内能将趋于最小值。
说着艾博士拿起一粒豆子放进了怪杯子里，用力摇晃起来。边摇晃杯子艾博士边解释说：这个豆子就代表了粒子的运动，杯子的摇晃速度就代表了系统所处的温度，越用力摇动杯子表示温度越高。杯壁上的很多小凹槽代表了不同的内能水平，越处于杯子上部的凹槽表示内能越高，越是处于杯子下部的凹槽表示内能越低，而杯子底部的几个凹槽就是内能最低的位置。当我们非常用力地摇晃杯子时，豆子在杯子里激烈地跳动，可能会出现在杯子的任何位置。如果我们缓慢地降低摇晃杯子的速度，由于摇晃的速度越慢，豆子越容易向下落，所以这种情况下，豆子总体上会趋向于落向下方。当我们最终停止摇动杯子时，豆子会大概率地落入到杯子底部的凹槽中，也就是内能最低的位置。小明你看，这个奇怪的杯子是不是跟退火现象非常像？
听艾博士这样介绍，小明高兴地说：用这个怪杯子类比退火现象太形象了，容易理解多了。
艾博士继续讲解说：当然引入这个怪杯子的目的只是为了帮助我们理解退火过程，为什么退火过程最终会趋于内能最小的状态，还必须从数学上给出信服的分析。同样的，为了帮助理解，在数学推导过程中会与怪杯子对应起来，以便帮助大家理解。
小明兴奋地说：这样就太好了，更容易理解了。
艾博士：如果以粒子的排列或者相应的内能表达金属所处的状态，在温度T下，金属所处的状态具有一定的随机性。一方面，物理系统倾向于内量较低的状态，另一方面，热运动又妨碍了系统准确落入低内能状态。
用怪杯子比喻的话，由于杯子处于摇晃状态，豆子落入到哪个凹槽中具有一定的随机性，但是由于豆子具有重量会倾向于落入较低的凹槽中，但是由于晃动的存在，又妨碍了豆子准确落入处于下方的凹槽。
对于这一物理现象，物理学家Metropolis给出了从状态i转换为状态j的准则：
如果E(j)≤E(i)，则状态转换被接受；
如果E(j)＞E(i)，则状态转移被接受的概率为：
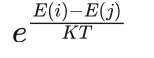（4.1）
其中E(i)、E(j)分别表示在状态i、j下的内能，T是绝对温度，K＞0是物理中的波尔兹曼常数。
Metropolis准则表达了这样一种现象：在温度T下，系统处于某种状态，由于粒子的移动，系统的状态发生微小的变化，并导致了系统内能的变化。如果这种变化使得系统的内能减少，则接受这种转换；如果变换使得系统的内能增加，则以一定的概率接受这种转换。概率的大小与温度有关，温度越高转换概率越大，温度越低转换概率越小。
这就相当于怪杯子中的豆子，一旦遇到一个低位置的凹槽就马上落入该凹槽，如果遇到一个高位置的凹槽，则以一定概率落入其中，概率的大小与杯子的晃动程度有关，晃动越激烈落入高位置凹槽的概率就越大，晃动越缓慢落入高位置凹槽的概率就越小。
在给定的温度T下，当进行足够多次的状态转换后，系统将达到一种热平稳状态。此时系统处于某个状态i的概率 Pi(T) 由Boltzmann分布给出：
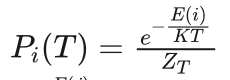（4.2）
其中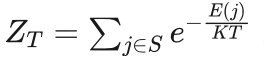 
为归一化因子，S是所有可能状态的集合。
对于怪杯子来说，如果我们保持晃动杯子的速度不变，则豆子在杯子里不停地跳动，一会落入这个凹槽中，一会落入那个凹槽中，如果时间足够长就会达到一种平稳状态，即落入每个凹槽的概率会达到一个稳定值。
做完怪杯子演示艾博士接着说：为了说清楚为什么退火过程最终会趋向于落入最低内能的状态，下面我们分以下4种情况，考察一下式（4.2）给出的温度T下落入状态i的概率随温度T的变化情况：
同一温度下两个内能不同的状态
高温下的情况
低温下的情况
当温度缓慢下降时的情况
（1）同一温度下两个内能不同的状态
艾博士问小明：假设i、j是怪杯子上的两个凹槽，并假定i的位置低于j的位置。当匀速晃动杯子时，豆子处于凹槽i、凹槽j的概率哪个更大呢？
小明回答说：豆子应该更倾向于落入位置低的凹槽吧？所以应该是处于凹槽i的概率大于处于凹槽j的概率。
艾博士：小明说的是对的。在退火过程中也存在类似的现象。在给定的温度T下，设有i、j两个状态，并假设两个状态的内能E(i)＜E(j)，我们比较一下落入状态i和状态j的概率的大小。
由式（4.2）有：
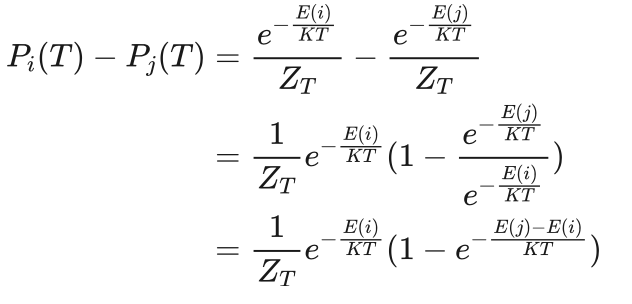(4.3)
由于E(i)＜E(j)，波尔兹曼常数K>0，绝对温度T>0，所以：
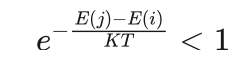
从而有：
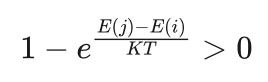
而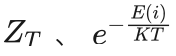 
也都是大于0的，所以有：
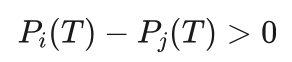
即：
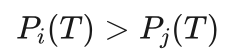(4.4)
上式说明，在温度T下落入低内能状态i的概率大于落入高内能状态j的概率。
从而得出结论：在任何温度T下，系统处于低内能状态的概率大于处于高内能状态的概率。
（2）高温下的情况
艾博士对小明说：你用力摇晃这个怪杯子，有多大力用多大力，观察一下豆子的情况。
小明按照艾博士说的，用力地摇晃起杯子，观察一会后说：当我用力地摇晃杯子的时候，豆子在里边到处乱跳，无论是杯子上边还是下边都能看到豆子，感觉豆子在任何地方的机会都差不多，看不出有什么差别。
艾博士：当你用力摇晃杯子的时候，就相当于高温情况下的退火过程，当温度足够高时，粒子落入任何状态的概率都是一样的。我们通过求解当温度T趋近于无穷时，落入状态i的概率可以得到这个结论。
当温度很高时，我们考虑当温度T趋于无穷大时的情况，由式（4.2）有：
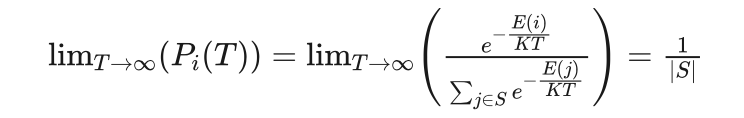（4.5）
其中|S|表示系统所有可能的状态数。由该结果可以看出，当温度趋于无穷大时，处于各个状态的的概率是均匀分布的，都是状态数分之一，与状态的内能大小无关。对于怪杯子来说，当摇晃的足够快时，无论凹槽在杯子的什么位置，豆子都会等概率落入其中。这与小明刚刚观察到的情况是一致的。
从而我们得出结论：当温度趋近于无穷大时，系统处于各个状态的概率相等，处于平均分布，与所处状态的内能无关。
（3）低温下的情况
艾博士：请小明再次做个实验，先是用力摇晃杯子，然后慢慢地降低摇晃的速度，看看最终当停止摇晃时，豆子会处在什么位置。
小明连续做了几次实验后说：只要我慢慢地降低速度，最终停止摇晃的时候，豆子基本都落入了杯子底部的凹槽中，也就是位置最低的凹槽中了。
艾博士：我们看看当温度很低时退火过程会是什么样的情况。当温度很低时，我们考虑当温度趋于绝对0度时的极限情况。
由式（4.2）有：
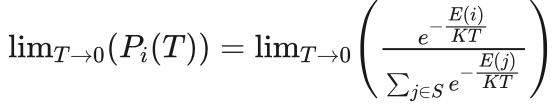（4.6）
设 Sm 表示系统最小内能状态的集合，Em 表示系统的最小内能。
小明：最小内能状态为什么用集合表示？会有多个内能最小的状态吗？
艾博士：就像怪杯子底部有几个一样的凹槽一样，这些凹槽的位置是一样高的。一个物理系统也可能有多个最小内能的状态，所以我们用集合 表示，而|Sm| 表示最小内能状态的数量。
小明：明白了，原来是这样的。难怪在前面介绍怪杯子的时候，强调在杯子底部有几个一样的凹槽。
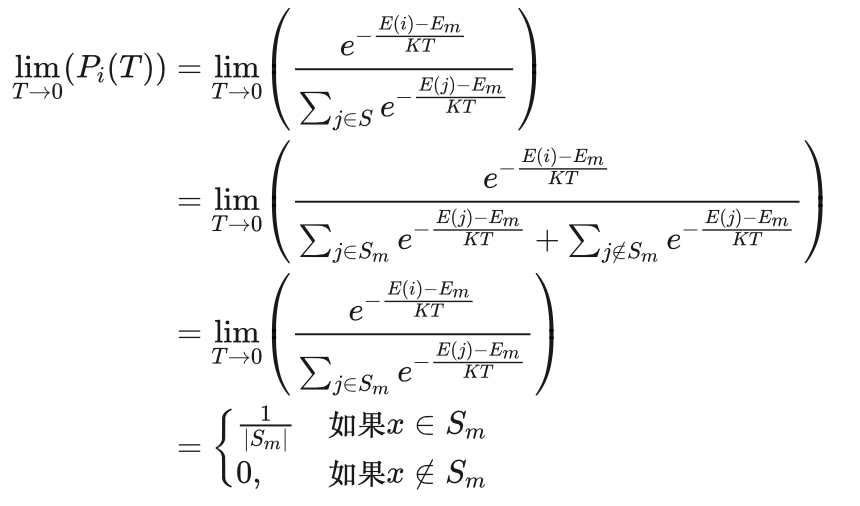
艾博士：为了求解上式的极限，我们对式（4.6）做个变换，分子、分母同乘以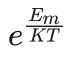 
后有：
（4.7）
在上面的推导过程中，由于T表示的是绝对温度，一定是大于0的，所以T趋近于0只能是从大于0的方向趋向于0，在推导过程中利用了这一点。
上面的推导结果说明，当温度趋近于绝对0度时，系统处于非最小内能状态的概率为0，处于某个最小内能状态的概率为最小内能状态数分之一。如果系统处于任何一个最小内能状态就属于处于最小内能状态的话，则系统处于最小内能状态的概率为1。
由此可以得出结论：当温度趋近于绝对0度时，系统以等概率趋近于几个内能最小的状态之一，而系统处于其他状态的概率为0。也就是说系统达到内能最小状态的概率为1。
小明：我明白了，这个结论说明了为什么退火过程最终会趋向于内能最小的状态。
（4）当温度缓慢下降时的情况
艾博士：小明你再摇晃怪杯子，这次看看摇晃速度稍微缓慢下降一点时，豆子会怎样变化？
这次实验做起来有些难度，下降速度不太好控制。当速度变化很小时，也难于观察豆子的变化情况。在艾博士的帮助和启发下，经反复实验、仔细观察之后小明终于有了结果。
小明总结说：当摇晃速度缓慢下降时，每下降一次摇晃速度，豆子的位置总体上趋向于向下一些，虽然还是在上下跳动，但是向上去的情况逐渐减少，而向下去的情况逐渐增多。
艾博士夸奖说：小明总结的很好，就是这样的结果。
为了考察退火过程温度稍微下降时的情况，我们计算一下处于状态i的概率对温度T的偏导数。因为偏导数反应了温度T时处于状态i的概率的变化趋势，我们看看该概率是如何变化的。
我们先计算处于状态i的概率对温度T的偏导数：
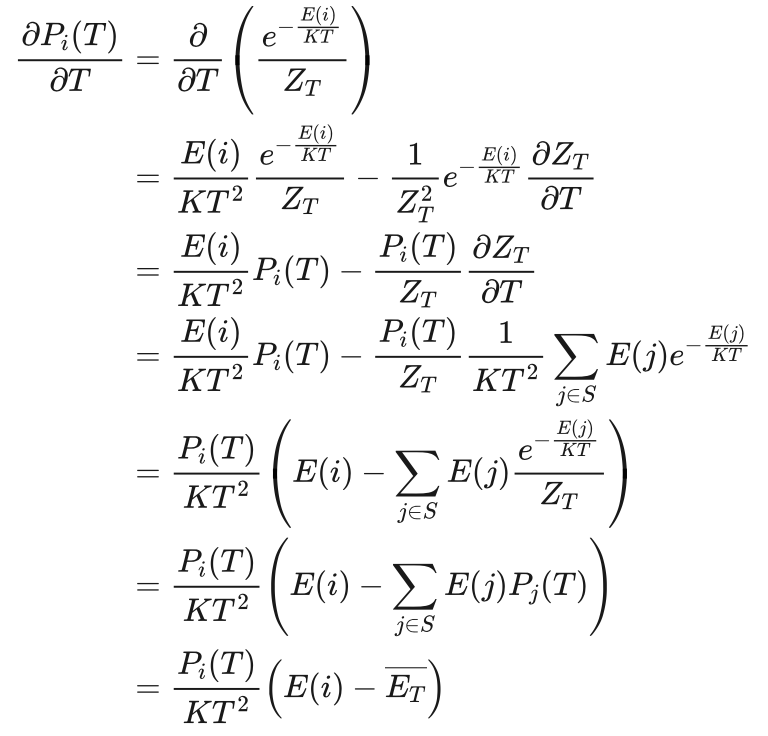（4.8）
其中： 
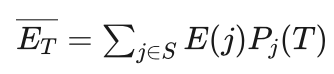（4.9）
是温度T下，各状态内能的平均值。
由于 Pi(T) 、K、T均大于0，因此由式（4.8），我们有：
（4.10）
也就是说，在温度T下，当状态i的内能大于平均值时，处于状态i的概率对温度T的偏导数大于0，而当状态i的内能小于平均值时，处于状态i的的概率对温度T的偏导数小于0。
小明：这个结果说明了什么问题呢？我还是看不太明白。
艾博士：为了讲解方便，我们将内能大于平均值的状态，也就是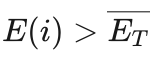 
的状态i，称作高能状态，而把内能小于平均值的状态，也就是 
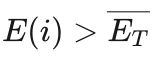的状态i，称作低能状态。注意这里的平均内能
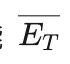是与温度T有关的，不同温度下的平均值可能不相同，因此一个状态属于高能状态还是低能状态，也是与温度T有关的，在一个温度T下的低能状态，在另一个温度下可能就是高能状态。
偏导数为概率Pi(T) 在T点的切线斜率，对于高能状态，温度T处的偏导数大于0，其切线如图4.13所示从左下到右上。在一个比较小的温度变化范围内，概率 Pi(T) 的变化趋势与切线一致，所以我们通过分析当温度从 T0 下降到 T1 时切线的变化获知概率 Pi(T) 的变化趋势。如图4.13所示，如果温度从 T0 下降到 T1 ，则系统处于状态i的概率从 Pi(T0) 下降到 Pi(T1) 。也就是说，当温度缓慢地下降一点时，处于高能状态的概率会随温度下降而下降。
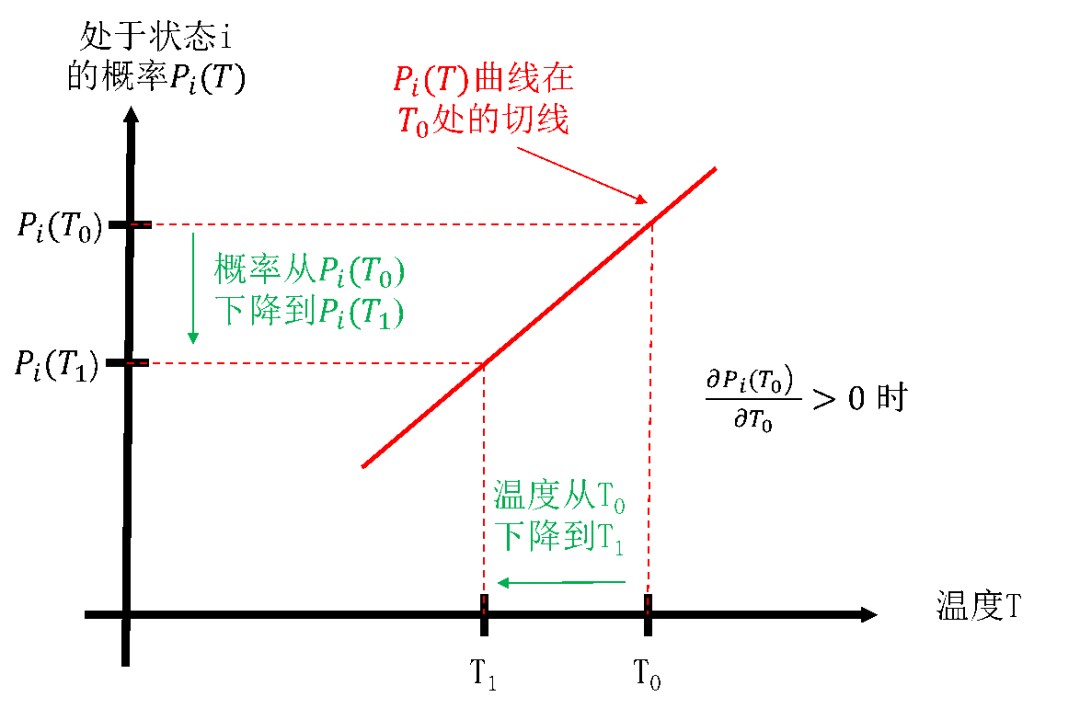
图4.13 处于高能状态的概率随温度下降而下降
同样地，对于低能状态，温度T处的偏导数小于0，其切线如图4.14所示从左上到右下。如图所示，如果温度从 T0下降到 T1 ，则系统处于状态i的概率从 Pi(T0) 上升到 Pi(T1) 。也就是说，当温度缓慢地下降一点时，处于低能状态的概率会随温度下降而上升。
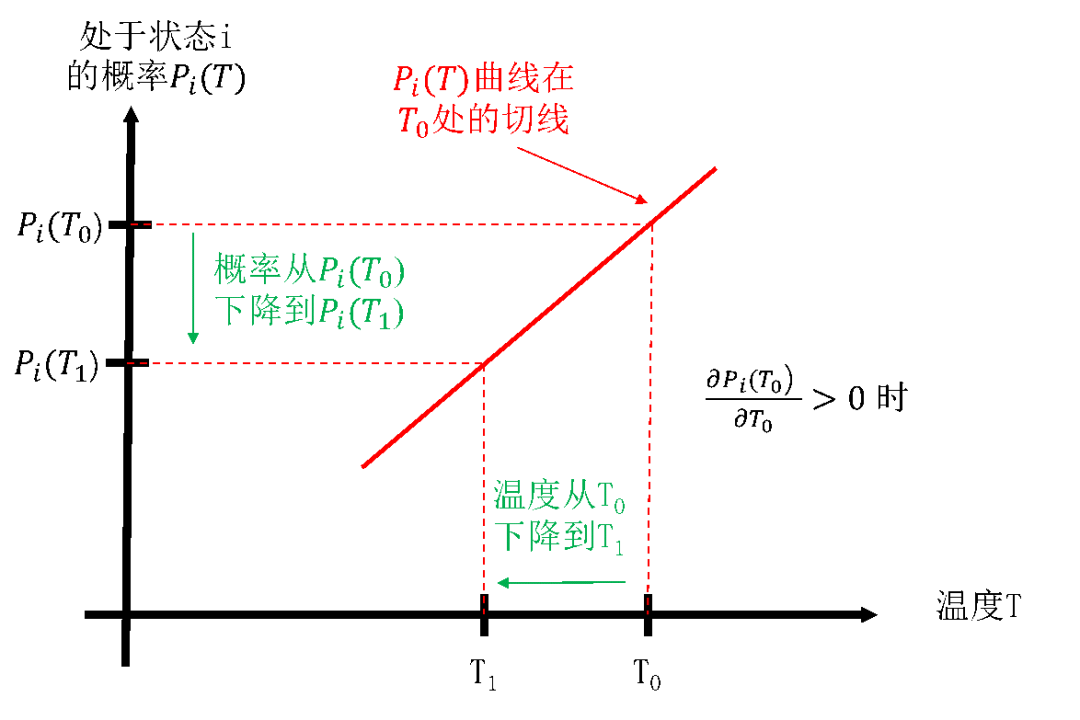
图4.14 处于低能状态的概率随温度下降而上升
从以上分析我们可以得出结论：系统落入高能状态的概率随温度T下降单调下降，而系统处于低能状态的概率随温度T下降单调上升。也就是说，系统处于低能状态的概率随着温度的下降单调上升，而系统处于高量状态的概率随着温度的下降单调下降。随着温度的缓慢下降，由于处于低能状态的概率越来越大，处于高能状态的概率越来越小，导致状态的内能平均值 随温度下降而下降，从而使得更多的状态属于高能状态，越来越少的状态属于低能状态。最终，当温度降低到趋近于绝对0度时，只有具有最小内能的状态才属于低能状态。这也从另一个角度说明了当温度趋近于绝对0度时，为什么系统处于最小内能状态的概率为1，这与我们前面的分析是一致的。
小明慢慢地体会着艾博士说的每一句话，思考了一会说：我明白了，以上4点从不同角度分析了处于某个状态i的概率及其变化情况，这4点也是相互有联系的，综合在一起构成了整个退火过程。比如开始时必须有足够高的温度，这样才可能让粒子充分运动。就好比晃动怪杯子，如果开始时不具备足够的晃动速度，偶然落入较高位置凹槽的豆子，可能由于晃动速度不够导致无法跳出凹槽，一直到慢慢停止晃动时豆子依然在这个凹槽里。还有如果温度不是缓慢下降而是下降速度比较快的话，由于粒子没有足够的交换时间，温度突然就降下来的话，系统也极大可能被“冻结”在高内能状态，失去向低内能状态转移的机会。比如刚开始怪杯子晃动的虽然足够快，但晃动速度下降比较快的话，豆子很有可能会停留在一个位置比较高的凹槽内而跳不出来。用我们前面做过的做弹簧实验也可以说明这一点，退火后的钢丝会变的很软，这是因为加热到通红的钢丝放在了室温下缓慢降温，最终降温到与室温一样。这样就完成了退火过程，使得原来具有弹性的钢丝处于了一种低内能状态，变得很软。当加工好弹簧之后，我们再次对弹簧加热到通红，然后直接放入到冷水中，这种突然降温，使得粒子来不及交换温度就降低到了几乎和冷水一样的低温，从而使得弹簧处于某个高内能状态，钢丝又恢复了已有的弹性。这其实就是退火的反过程——淬火过程。
艾博士：小明总结的很好。梳理一下以上4点内容，我们可以得出如下结论：
在高温下，系统基本处于无序的状态，以等概率处于各个不同的状态。在给定的温度下，系统处于低能状态的概率大于系统处于高能状态的概率，这样在同一温度下，如果系统交换的足够充分，则系统会趋向于处于较低内能的状态。随着温度的缓慢下降，系统处于低能状态的概率逐步增加，而处于高能状态的概率逐步减少，使得系统各状态内能的平均值随温度的下降单调下降，而只有那些内能小于平均值的状态，其概率才会随温度下降增加，其他状态均随温度下降而下降。这样导致状态的内能平均值也随温度下降而下降。因此，随着内能平均值的逐步下降，低能状态逐步减少，当温度趋于绝对0度时，只剩下那些具有最小内能的状态，系统处于其他状态的概率趋近于0。因此最终系统将以概率1处于最小内能状态。
小明：听您讲了这么多，基本明白了其中的大概思想，回去后我再好好复习复习，内容有些多，还需要整理消化一下。我觉得退火过程最重要的几点是：具有足够高的初始温度，温度下降足够缓慢，随着温度的缓慢下降，当最终趋于绝对0度时，系统将以概率1处于最低内能的状态。
艾博士赞许地点点说：能意识到这几点的重要性，说明你基本听懂了。
接下来艾博士总结说：最后我们再总结一下退火现象的要点：当温度处于较高温度时，系统基本以等概率处于任何一种状态。当温度缓慢下降时，系统处于低能状态的概率增加，而处于高能状态的概率下降。当温度缓慢下降逐渐趋近于绝对0度时，系统以概率1处于内能最小的状态。在这个过程中必须满足以下三个条件：
（1）初始温度必须足够高；
（2）在每个温度下状态的交换必须足够充分；
（3）温度T的下降必须足够缓慢。
在这三个条件都满足的情况下，系统才有可能以概率1处于内能最小的状态。实际上，即便系统最终没有落入内能最小的状态，只要满足以上几个条件，一般也会处于一个内能比较小的状态。
小明：经过您的以上讲解，终于明白了为什么在我们做弹簧实验时，要先将钢丝烧的通红，然后再在室温下慢慢冷却，虽然最后没有降温到绝对0度，但相对于烧得通红的钢丝来说，室温已经很低了。这样处理后，钢丝就处于一个很低的内能状态了，所以会变得很软，从而很容易加工了。
艾博士：就是这个道理。
小明读书笔记
将金属加热到高温后再慢慢地冷却下来，金属将处于一个内能最小的状态，这就是物理中的退火过程。
为什么退火过程会达到内能最小状态呢？可以将退火过程类比做一个“怪杯子”，杯子的摇晃程度相当于温度，杯壁上的一些小凹槽相当于系统所处的状态，凹槽的不同位置代表了不同的内能，杯子中的豆子相当于粒子的运动。怪杯子形象地“演示”了退火现象。
退火现象的几个性质：当处于高温时，系统几乎以等概率处于不同内能的状态；当温度缓慢下降时，处于高能状态的概率下降，而处于低能状态的概率上升；在温度不变时，系统处于低能状态的概率高于处于高能状态的概率；当温度趋近于绝对0度时，系统以概率1处于内能最小的状态。
退火过程必须满足的三个条件：初始温度必须足够高，每个温度下状态的交换必须足够充分，温度下降必须足够缓慢。只有这样才能使得当温度趋近于绝对0度时，系统以概率1趋近于内能最小状态。
在退火过程中，状态交换时按照概率1接受低内能状态，按照概率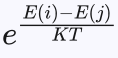 
接受高内能状态，这正是改进局部搜索算法所希望具有的性质。
未完待续