第四篇 如何用随机算法求解组合优化问题（二）
清华大学计算机系 马少平
第二节：局部搜索算法
艾博士：在讲解求解组合优化问题的随机算法之前，我们先从局部搜索算法开始讲起。
在第三篇中我们讲解过寻找最佳路径的A*算法。A*算法寻找的是从初始位置a到达目标位置b的最佳路径，也就是说我们知道目标位置，也知道每个节点达到目标位置最佳路径的估计值，也就是启发函数h(n)。从某种程度来说，算法“看到”的是“全局”信息，从而最终找到的也是全局最优解。
小明：这么说像A*算法这类的最短路径算法就不能用于求解组合优化问题了吗？
艾博士：也不是不可以，只要能定义启发函数h(n)就可以用A*算法求解，问题是能否定义一个有效的启发函数。
局部搜索指的是看不到全局信息，也不知道目标的具体位置，对于组合优化问题来说，目标可能只是满足约束条件的最优解。比如对于旅行商问题来说，求解的是满足“每个城市必须去一次、每个城市只能去一次、最后再回到出发城市”的最短路径。对于这样的问题，只能利用局部信息进行搜索。比如爬山法就是典型的局部搜索算法。
小明：什么是爬山法呢？
艾博士：假设有一座山，想爬到山峰上去。如果你时刻能看到山峰在哪里，就可以大概向山峰方向前进，这样就可以爬到山峰上去。这属于全局搜索。
如果蒙上你的眼睛，让你看不到山峰在哪里，或者因为山林太茂密，看不到山峰在哪个方向，只能看到眼前的局部地理情况，如何爬到山峰上去呢？
小明：这看起来有些难度。
艾博士：在蒙上眼睛的情况下，看不到任何东西，假设给你一根拐杖，拐杖是探索周围环境的唯一工具。在这种情况下，唯一可以依赖的工具就是这根拐杖。
小明：利用这根拐杖就可以爬到山顶吗？
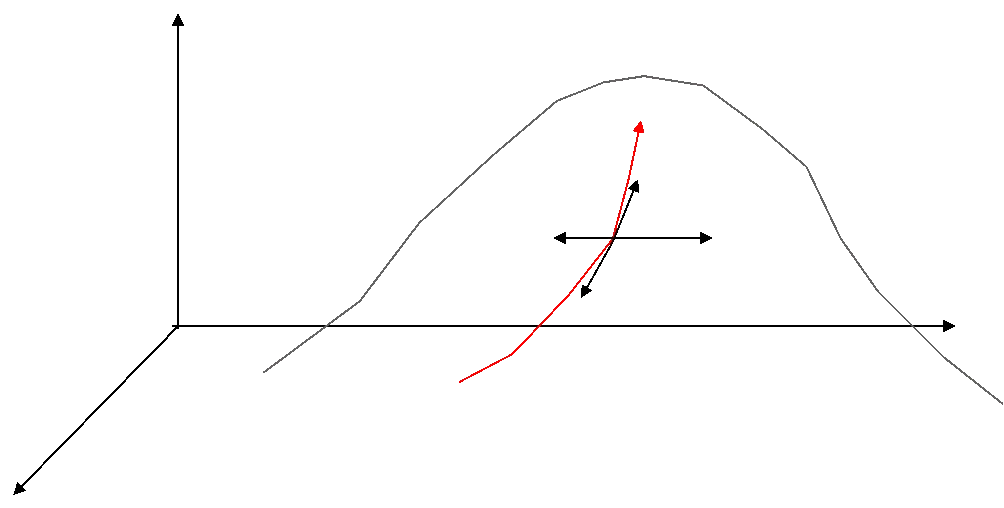
图4.1 爬山法示意图
艾博士：一种可行的方法是，先原地不动，在身体周围用拐杖进行试探，看哪个方向更高一些，然后向高的方向迈进一步。重复刚才的动作，一步一步地向高的方向移动，就有可能到达山顶了。如果山坡是光滑的，并且只有一个山峰，这应该是可以到达山峰的一种办法。
小明：这样似乎是可以的。
艾博士：我们总结一下爬山法，首先我们站在一个位置上，在该位置所在的一个范围内，找一个最高的位置，也就是最好的位置，然后移动到该位置，将该位置作为新的起点，反复重复以上动作。
这里的范围，就是拐杖所能触及的、以拐杖为半径的一个圆，我们称作邻域。但是组合优化问题变量一般是离散的，没有半径的概念。一般来说经过简单变换后得到的一个解为一个邻居，所有邻居的集合就是邻域。下面我们结合具体问题举例说明邻居和邻域的概念。
（1）四皇后问题
艾博士：在4×4的棋盘上，如何摆放4个皇后，使得棋盘上任何一条直线上最多有一个皇后，也就是任何一行、任何一列，以及任何对角线上，都最多只能摆放一个皇后。我们用一个整数的序列表示棋盘上皇后的位置，其中整数在序列中的位置表示皇后所在的行，而该整数值表示皇后所在的列。例如（2,4,1,3）表示第1行第2列、第2行第4列、第3行第1列、第4行第3列摆放有皇后，也就是四皇后问题的一个解。如果我们采用任意交换两个皇后的位置的方法获得其邻居，则（2,4,1,3）的所有邻居，也就是邻域为：
{(4, 2, 1, 3), (1, 4, 2, 3), (3, 4, 1, 2), (2, 1, 4, 3), (2, 3, 1, 4), (2, 4, 3, 1)}
小明：原来邻域指的是这个意思，以一个解为基础，采用简单变换的方法获得的一组解就是该解的邻域。
（2）旅行商问题
艾博士：我们用城市的一个序列表示旅行商问题的一个可能路径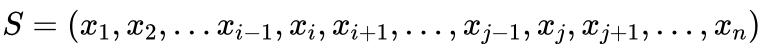 
，可以通过任意交换两个城市xi 、xj 在序列中的位置得到S的邻居S’如下所示：
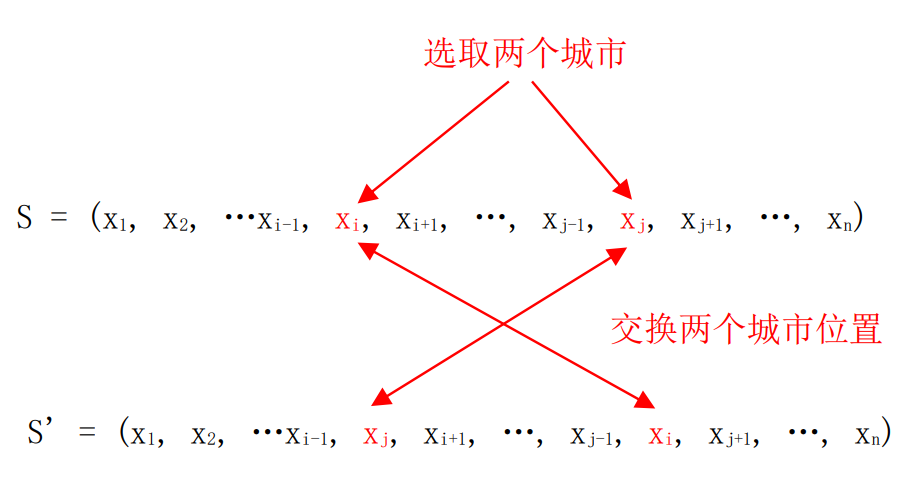
交换前后的路径变化情况如图4.2所示，这种获得邻居的方法称为“常规交换法”。
图4.2 旅行商问题通过常规交换法获得邻居示意图
对于旅行商问题也可以采取“逆序交换法”获得邻居。对于任意两个城市xi 、xj ，我们可以通过逆序排列 xi、xj 两个城市之间的城市次序来得到S的邻居S’如下所示：
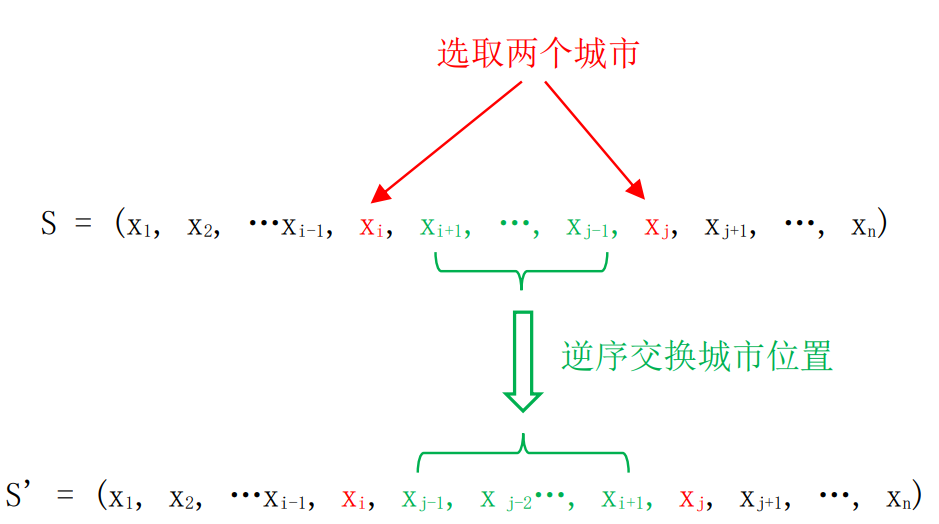
所谓的逆序交换法，就是对于两个城市xi 、xj 之间的城市，原来的排列次序是 xi+1,...,xj-1,经逆序交换后，排列变成了xj-1,xj-2,...,xi+1 。
讲到这里艾博士提醒说：注意这里 xi、xj 两个城市的位置并不发生变化，而是这两个城市之间的城市发生了逆序变化。交换前后的路径变化情况如图4.3所示。
图4.3 旅行商问题通过逆序交换法获得邻居示意图
小明：对于旅行商问题您介绍了两种不同的获得邻居的方法，是不是可以说获取邻居的方法并不是唯一的，可能有不同的变换方法。
艾博士：是的。有了邻域的概念之后，我们就可以将爬山法推广为局部搜索算法求解组合优化问题。
小明：如何推广呢？
艾博士：对于局部搜索来说，首先定义一个指标函数f，该函数相当于山峰的高度，一个初始的解，相当于在山上的位置，每个解可以计算出其指标函数f，也就是该位置所处的高度。然后按照给定的求解邻域的方法获得邻域，从邻域中取一个指标函数f最大的邻居作为一个新的位置。
小明：这看起来跟爬山法差不多啊。
艾博士：确实差不多，本来爬山法就是局部搜索算法的一种。由于爬山法更容易理解，所以我们从爬山法开始讲起。
艾博士问小明：小明，你想想局部搜索算法应该什么时候结束呢？
小明不加思考地回答：指标函数最大了就可以结束了。
艾博士笑了笑说：小明你想的有点简单了，我们确实要求指标函数最大值，但是我们怎么知道一个指标函数是否最大呢？
小明：是啊，一般来说确实不知道啊。
艾博士：还是以前面说的蒙上眼睛爬山为例。如果真要你去这样爬上，由于被蒙上了眼睛，你会什么时候结束爬山呢？
小明思考了一会说：在爬山过程中，我会每次用拐杖四周探索，探索到一个高点就走过去，依次这样做，一点点爬高。如果走到了某个位置，发现用拐杖如何探索都找不到比自己所处位置高的点了，我就会停止，因为眼睛被蒙上了，看不到周围的环境，用拐杖也找不到更高的地方，只好到此停止了。
艾博士：正是这样的，当在一个邻域内找不到更好的解，也就是指标函数f更大的解时，算法就可以结束了。
小明：但是这样就一定能找到最优解吗？
艾博士：一般情况下是不能保证找到最优解的，但是如果山峰只有一个高峰，而且山坡也是非常平滑时，是可以找到最高峰的。
小明：一般的组合优化问题满足这样的条件吗？
艾博士：一般的组合优化问题并不满足这一条件，这也是为什么说组合优化问题求解比较复杂的原因。
小明：这样的话，局部搜索算法有什么意义呢？
艾博士：有一些改进的办法，我们将在后面介绍。下面我们先给出局部搜索算法的一般性描述。在该算法中，并不像爬山法那样，每次从邻域中找出一个最好的结果，而是将邻域分成若干部分，每次从其中一部分中找出一个最好的结果，如果该结果比当前结果好的话就接受，否则再看邻域的其他部分，直到所有部分的最好结果都不如当前结果好为止，算法结束。局部搜索算法可以求最大值，也可以求最小值，一般在描述局部搜索算法时用的是求最小值，下述算法也同样假设求最小值，很容易将其修改为求解最大值。
在算法中，f(x)表示指标函数，算法的目的就是求f(x)取最小值时x的取值。变量 xb 为到目前为止得到的最好解， N(xb) 为计算xb 的邻域。
局部搜索算法具体描述如下：
局部搜索算法（Local Search）
1、随机的选择一个初始的可能解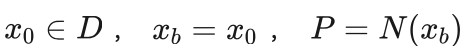
2、如果不满足结束条件，则
3、Begin
4、选择P的一个子集P'， xn 为P'中的最优解
5、如果 f(xn)<f(xb)，则 xb＝xn ，P=N(xb) ，转2；
6、否则P = P–P'，转2。
7、End
8、输出计算结果
9、结束
小明：算法大概看懂了，但是最好能结合一个具体的例子讲解一下。
艾博士：好的，下面我们就举一个5城市旅行商的例子。5城市旅行商问题如图4.4所示，共有A、B、C、D、E等5个城市，A为出发城市，遍历其他4个城市之后还要回到A城市，图中的数字给出了任意两个城市间的距离。
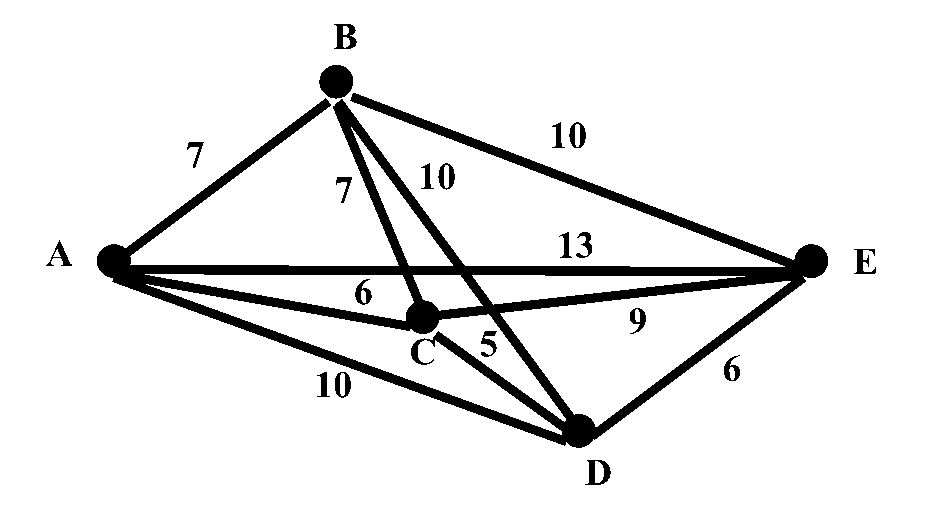
图4.4 5城市旅行商问题
艾博士：我们用局部搜索算法求解该问题，首先要定义指标函数。小明，你认为对于这个问题指标函数应该怎么定义呢？
小明想了想说：5城市旅行商问题就是求走遍5个城市长度最短的路径，可以用路径长度作为指标函数吧？
艾博士：是的，指标函数与所求的问题相对应，对于旅行商问题路径长度就是指标函数。下面我们一步步地按照局部搜索算法求解该旅行商问题。
首先我们先生成一个初始解，假设为 x0=(A,B,C,D,E) ，表示旅行商行走的一条路径A-B-C-D-E-A，注意，最后要回到出发城市A。当前只有x0 一个结果，所以当前最好结果为 xb=x0 。计算 xb 的指标函数值 f(xb)=7+7+5+6+13=38 。我们按照交换两个城市位置的方法得到 xb 的邻域P，P中每个元素都是一个解，即一条可能的行走路线。由于A是出发城市，我们只对其他城市做了交换，A保持在第一个位置不动。
P={(A,C,B,D,E),(A,D,C,B,E),(A,E,C,D,B),(A,B,D,C,E),(A,B,E,D,C),(A,B,C,E,D)}
按照局部搜索算法，每次从P中选取其中的P’部分，我们假设每次只选取一个解，用 表示。
第一次循环：
从P中随机选择一个解，假设为 xn=(A,C,B,D,E) ，则 f(xn)=6+7+10+6+13=42 。由于f(xn)>f(xb) ，不是一个更好的解，所以不接受该结果，将 xn 从P中删除，有：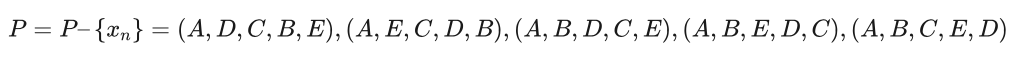
第二次循环：
从P中随机选择一个解，假设为xn=(A,D,C,B,E) ，则 f(xn)=10+5+7+10+13=45 。由于f(xn)>f(xb) ，也不是一个更好的解，不接受给结果，将 xn 从P中删除，有：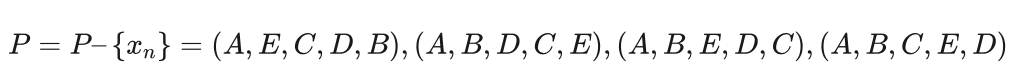
第三次循环：
从P中随机选择一个解，假设为xn=(A,E,C,D,B) ，则f(xn)=13+9+5+10+7=44 。由于 f(xn)>f(xb) ，还是没有得到更好的解，同样不接受该结果，将xn 从P中删除，有：
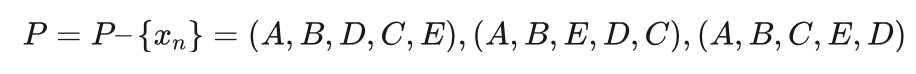
第四次循环：
从P中随机选择一个解，假设为xn=(A,B,D,C,E) ，则 f(xn)=7+10+5+9+13=44 。由于 f(xn)>f(xb) ，不是一个更好的解，不接受该结果，将 xn 从P中删除，有：
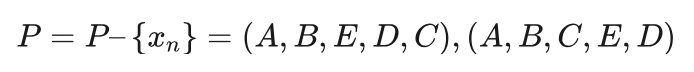
第五次循环：
从P中随机选择一个解，假设为 xn=(A,B,E,D,C) ，则f(xn)=7+10+6+5+6=34 。由于 f(xn)<f(xb) ，这次得到了一个目前为止最好的解，接受该结果，更新 xb=(A,B,E,D,C)。
重新计算 xb 的邻域P：
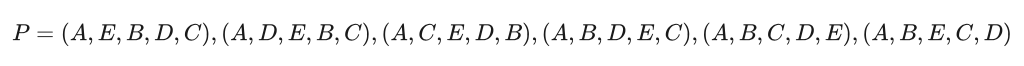
第六次循环：
从P中随机选择一个解，假设为 xn=(A,E,B,D,C) ，f(xn)>f(xb) ，由于 ，有：
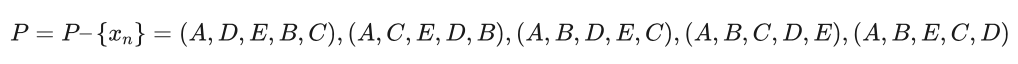
第七次循环：
从P中随机选择一个解，假设为xn=(A,D,E,B,C) ， f(xn)=39 ，由于f(xn)>f(xb) ，有：
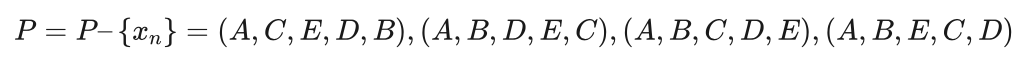
第八次循环：
从P中随机选择一个解，假设为xn=(A,C,E,D,B) ，f(xn)=38 ，由于 f(xn)>f(xb) ，有：
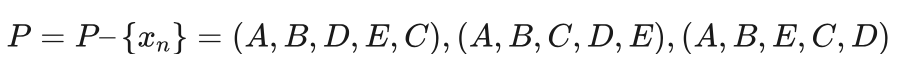
第九次循环：
从P中随机选择一个解，假设为xn=(A,B,D,E,C) ，f(xn)=38 ，由于 f(xn)>f(xb) ，有：
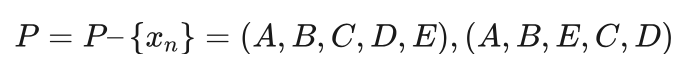
第十次循环：
从P中随机选择一个元素，假设为xn=(A,B,C,D,E) ，f(xn)=38 ，由于 f(xn)>f(xb) ，有：
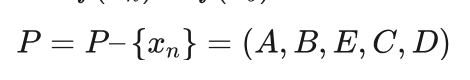
第十一次循环：
从P中随机选择一个，假设为 xn=(A,B,E,C,D) ，f(xn)=41 ，由于f(xn)>f(xb) ，有：
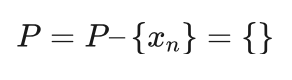
经过十一次循环之后，由于当前得到的最好解 的所有邻居都试探了一遍，P等于空，说明xb的邻域中不存在比 xb还好的解了，算法结束，而从得到当前最好解为 xb=(A,B,E,D,C) ，其指标函数 f(xb)=34 。
听艾博士讲解完例题，小明问到：看起来局部搜搜算法效果挺好吗，这个解是路径最短的解吗？
艾博士：这个解刚好是该5城市旅行商问题的最佳解，但是一般情况下，局部搜索只是找到一个局部最优解，并不能保证找到全局最优解，与很多因素有关，这也是局部搜索算法存在的问题。
艾博士接着说：小明，我们下面再举一个用局部搜索算法求解百万皇后问题的例子。
小明：百万皇后问题？我没有听错吧？真是一百万个皇后？
艾博士：确实没有听错，就是在一百万乘一百万大小的棋盘上，如何摆放一百万个皇后的问题。以前在第三篇中我们介绍过用深度优先搜索算法求解四皇后问题，当皇后数比较多时，深度优先搜索算法就有些无能为力了，别说是一百万个皇后，就是一百个皇后都比较困难。
小明有些疑惑地说：皇后问题不是个最优化问题啊，也可以用局部搜索算法求解吗？
艾博士：皇后问题确实不是一个最优化问题，但是我们也可以把它转化为一个最优化问题求解。
小明很感兴趣地问到：这倒是一个很有意思的求解问题的思路，怎么转化呢？
艾博士：我们可以定义一个指标函数，如果这个指标函数的最优解刚好对应皇后问题的一个解，就可以用局部搜索算法求解了。
比如我们可以这样定义指标函数：棋盘上皇后的冲突数。皇后问题要求棋盘上任何一条直线上都只能有一个皇后，无论是横、竖、还是斜线都是如此。我们定义棋盘上任意两个皇后在一条直线上，就是一次冲突，冲突数就是发生冲突的总次数。
例如在图4.5中，A、B、C、D为皇后，A与D是一次冲突，D与A也是一次冲突，B与C是一次冲突，C与B是一次冲突，所以冲突数为4。
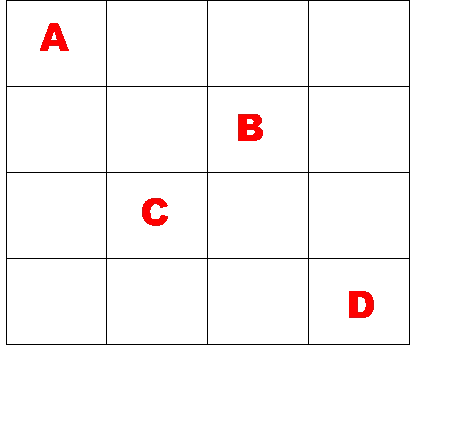
图4.5 皇后问题冲突数计算示意图
满足条件的皇后问题的解应该无任何皇后发生冲突，所以冲突数为0，其他情况下冲突数均大于0，所以皇后问题就转化为了求冲突数最小的问题。
小明：经过这样转换后，皇后问题就变成了求最小值的最优化问题了。有意思，又掌握了一种求解问题的方法。
艾博士：为了求解方便，我们采用前面曾经介绍过的一种皇后问题的表示方法。我们用一个整数的序列表示棋盘上皇后的位置，其中整数在序列中的位置表示皇后所在的行，而该整数值表示皇后所在的列。例如（2,4,1,3）表示第1行第2列、第2行第4列、第3行第1列、第4行第3列摆放有皇后，也就是四皇后问题的一个解。
用局部搜索算法求解百万皇后问题的思想非常简单，开始时先随机地在每行每列摆放一个皇后作为初始解，这一点并不难做到。如果冲突数为0，则求解结束，得到了一个解。如果冲突数不为0，则任选两个皇后交换其位置，相当于得到了当前解的一个邻居。如果交换位置后冲突数是下降的，则接受该解。如果交换后冲突数上升，则放弃此次交换，再任选两个皇后做交换。重复以上过程，直到冲突数为0算法得到一个解结束，或者当所有交换完成后冲突数仍不下降，说明进入了局部最小值。这种情况下，我们放弃此次求解，再重新开始做一次局部搜索，直到得到了一个冲突数为0的解为止。
采用局部搜索算法求解百万皇后问题的算法如下：
皇后搜索算法（Queen Search）
以整数序列表示皇后在棋盘上的位置。
1、随机地将n个皇后分布在棋盘上，使得棋盘的每行、每列只有一个皇后；
2、计算皇后间的冲突数conflicts；
3、如果冲突数conflicts等于0，则转（7）
4、任选两个皇后交换他们在序列中的位置，相当于两个皇后交换了所在的行而列不变；
5、如果交换后的冲突数conflicts减少，则接受这次交换，更新冲突数conflicts，转3；
6、如果陷入了局部极小，既交换了所有的皇后后，冲突数仍然不能下降，则转1；
7、输出结果
8、结束。
听完艾博士的讲解小明攒到：这么简单的算法竟然可以求解百万皇后问题？也真是神奇啊。
艾博士：之所以局部搜索算法可以求解百万皇后问题，主要是利用了皇后问题的一个特点。我们通过定义指标函数为冲突数将皇后问题转化为最优化问题，而皇后问题的解对应的指标函数为0，也就是指标函数的最小值。所以当用局部搜索算法求解时，由于我们已经知道了最优值是0，当求解的局部最优值不等于0时，我们可以放弃此次求解，再重新开始求解，直到找到了最优值为0的解为止。但是对于一般的组合优化问题，我们并不知道最优解是多少，所以也就不能判断所求解的局部最优解是否是我们希望得到的全局最优解，所以用局部搜索算法直接求解一般的组合优化问题会存在很多问题，这也是组合优化问题难以求解的原因之一。
小明读书笔记
局部搜索算法试图利用局部信息搜寻全局最优解。爬山法是一种典型的局部搜索算法，利用“拐杖”探测到的局部信息一点点爬向山峰。当具有多个山峰时，爬山法不能保证找到全局最优解。
“拐杖”所能探索的范围，也就是以拐杖为半径形成的一个圆称作邻域，邻域由若干个邻居组成。在组合优化问题中没有半径的概念，邻居通过简单变换获得，邻居的集合构成了邻域。对于旅行商问题，可以通过常规交换法或者逆序交换法获得邻居。每个邻居对应一个可能的解。
有了邻域的概念后，就可以将爬山法推广到求解一般的组合优化问题的局部搜索算法。所谓局部搜索算法，就是每次在邻域内随机选择一个邻居，也就是解，如果该解好于当前最好解，则接受该解，相当于向山上爬了一步，否则从邻域中删除该解，再选择邻域中的其他解。重复以上操作，直到邻域被删空也没有找到一个更好的解为止。
同爬山法一样，局部搜索算法不能保证找到全局最优解。
有些问题本身并不是最优化问题，但也可以将其转换为最优化问题求解。比如皇后问题，通过定义皇后的冲突数可以将皇后问题转化为求解冲突数最小问题，也就是冲突数为0时的解。利用皇后问题事先可以知道其最小值为0的特点，有研究者利用局部搜索算法实现了求解百万皇后问题。
未完待续