第五篇 统计学习方法是如何实现分类与聚类的(三)
清华大学计算机系 马少平
第三节:决策树
——ID3算法
艾博士:我们在对事物进行分类时,常常先用某个特征先划分成几个大类,然后再一层层的根据事物特点进行细化,直到划分到具体的类别。
比如,根据饮食习惯可以判断是哪个地方的人。可以先根据是否喜欢吃辣的,划分成喜欢吃辣的和不喜欢吃辣的两大部分。如果是喜欢吃辣的,则可能是四川人或者湖南人,再根据是否喜欢吃麻的这一点,区分是四川人或者是湖南人。而对于不喜欢吃辣的这一部分,如果喜欢吃甜的,则可能是上海人。如果不喜欢吃甜的,但喜欢吃酸的,则可能是山西人,否则就可能是河北人。
这一决策过程,我们可以表示为如图5.7所示。由于其形式类似于数据结构中的一棵树,所以被称作决策树。小明了解什么是树结构吧?
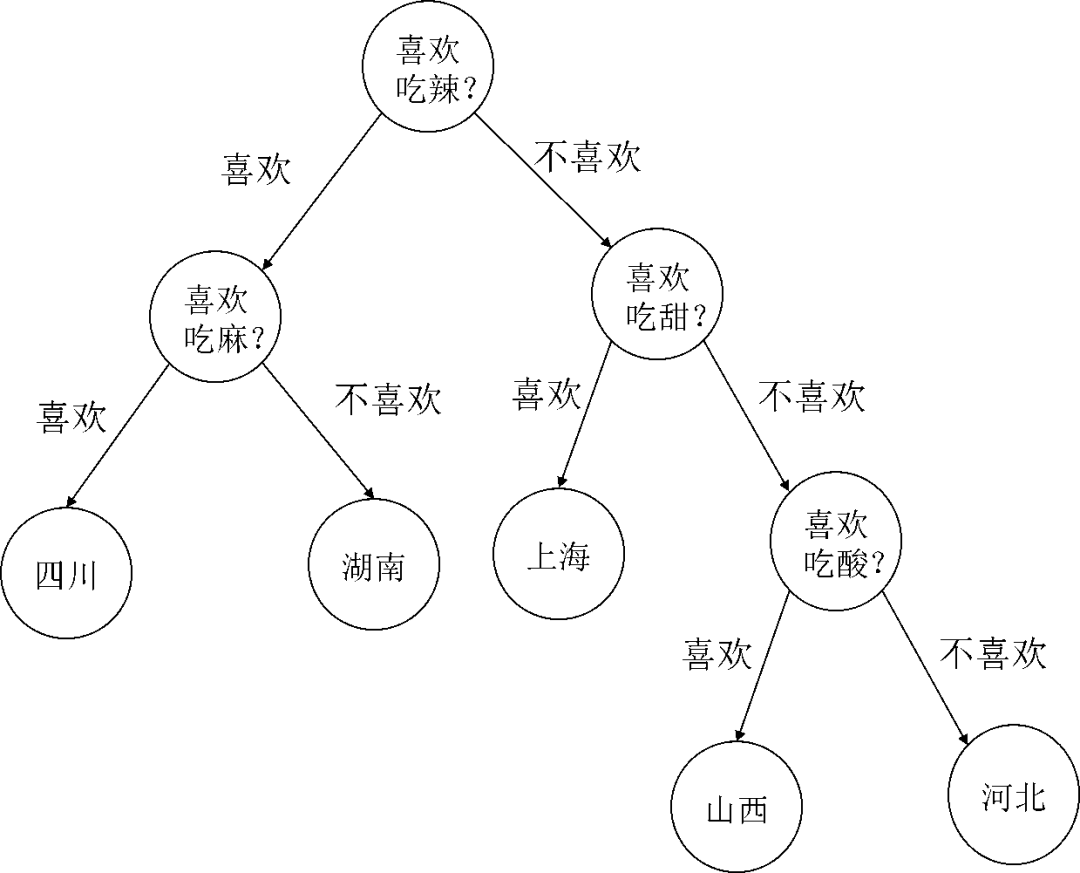
图5.7 决策树示意图
小明:我在数据结构中学习过树结构,这是一种常用的数据结构。图中的圆圈称作节点,节点具有层次性,是一层一层从上到下生成出来的。直接连接在一个节点下面的几个节点称作上面这个节点的子节点,而上面这个节点称作这几个子节点的父节点。子节点和父节点都是相对的,一个父节点可能是其他节点的子节点,同样的,一个子节点也可能是其他节点的父节点。比如图5.7中,节点“喜欢吃酸”是节点“山西”和节点“河北”的父节点,同时又是节点“喜欢吃甜”的子节点。图中最上面的节点,也就是没有父节点的节点,称作根节点。而图中最下面的节点,也就是那些没有子节点的节点,称作叶节点。比如图5.7中,节点“喜欢吃辣”就是这棵树的根节点,而节点“四川”、“湖南”、“上海”、“山西”和“河北”都属于叶节点。
艾博士:小明解释得很全面,几个重要的概念都介绍到了,我们会用到这些概念。
决策树是一种用于分类的特殊的树结构,其叶节点表示类别,非叶节点表示特征,分类时从根节点开始,按照特征的取值逐步细化,最后得到的叶节点即为分类结果。
小明:决策树这种方法看起来倒是比较直观,关键是如何建立这个决策树吧?
艾博士:是的。对于同一个问题,特征使用的次序不同,就可以建立多个不同的决策树,比如前面这个例子,也可以建立如图5.8所示的决策树。这就遇到了一个问题:如何评价一个决策树的好坏,因为我们总是希望建立一个最好的决策树。
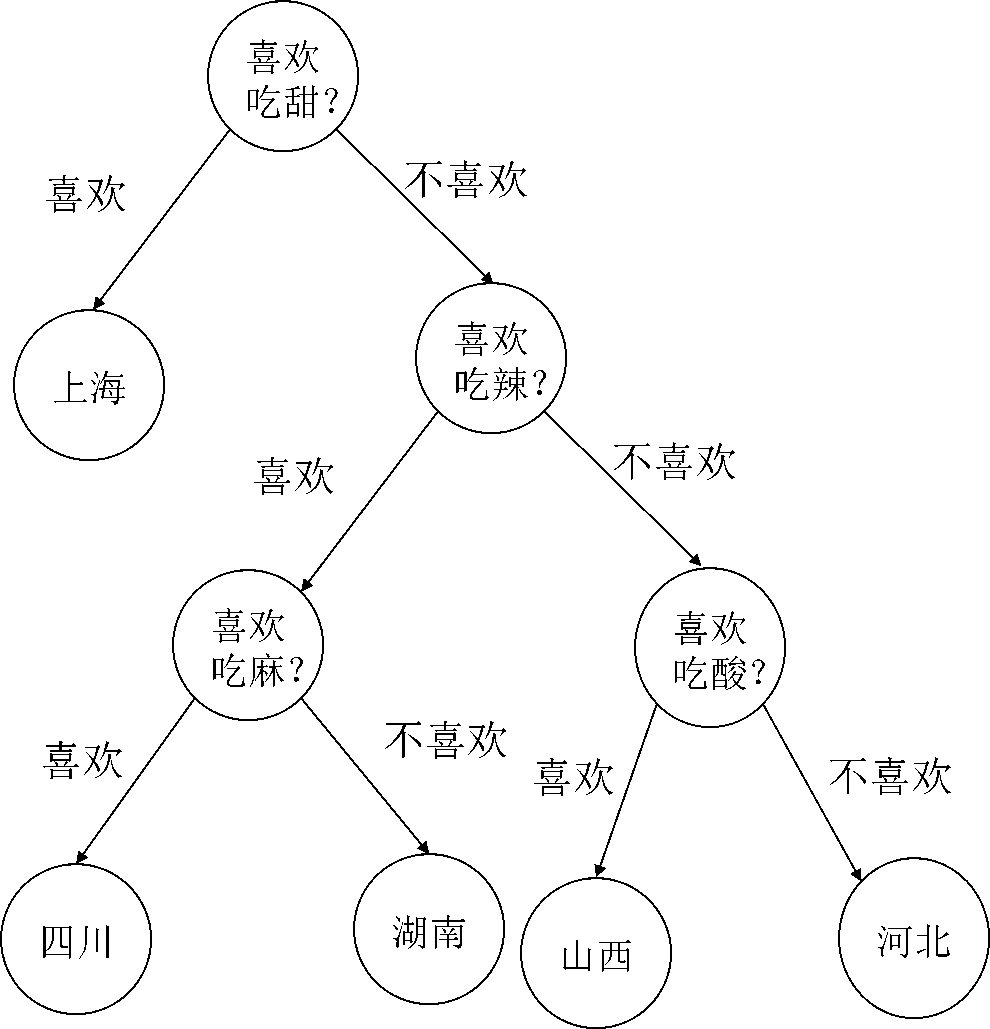
图5.8 决策树示意图
小明:俗话说,是骡子是马拉出来溜溜。能不能采用测试的方法?利用一些测试数据,测试每一个决策树的分类性能,哪个决策树的性能好,就选用哪个。
艾博士:的确是一个办法。但是这里存在一个问题,当特征数量比较多时,可能建立的决策树数量是非常多的,又遇到了组合爆炸问题。我们不可能把所有可能的决策树都建立起来,一个一个去测试以便找到一个最好的决策树。
小明有点不好意思地说:我又把问题想简单了。
艾博士:为了建立一个决策树,首先要有一个供训练用的数据集,数据集是建立决策树的依据。我们建立的决策树希望尽可能满足两个条件,一个条件是与数据集的矛盾尽可能小,也就是说,用决策树对数据集中的每个样本进行分类,其结果应该尽可能与样本的标注信息一致。另一个条件是在使用该决策树进行实际分类时,正确率尽可能高。后者称作泛化能力,泛化能力越强实际使用分类效果就越好。
听到这里小明急忙问到:难道决策树的分类结果不是应该与训练数据集的标注信息完全一致吗?为什么是尽可能一致呢?
艾博士解释说:可能有多个原因做不到完全一致,比如采用的特征不合理或者不完备,利用这些特征就做不到与数据集完全一致的分类,或者数据集本身具有一定的噪声,有些标注信息有错误,这种情况下不一致反而是正确的,一致了反而会有问题。还有就是数据集中的一些样本比较特殊,代表性不强,如果强制对这类样本做正确分类,其结果可能会造成决策树泛化能力下降。后面我们会看到,我们有时会人为地加大决策树分类结果与数据集的不一致性,以便提高决策树的泛化能力。
小明:竟然还会有这样的问题,比较有意思,期待着后面的讲解。
艾博士:既然不可能一个一个去测试每一个可能生成的决策树,就要看看是否有什么办法帮助我们建立一个比较好的决策树,即便不一定是最优的,但是也是一个比较好的。
首先我们先看看如何建立一个与数据集尽可能一致的决策树,先从这个角度考虑如何构建决策树问题。
在决策树中,按照特征的不同取值,可以将数据集划分为不同的子集,不同的决策树就是使用特征的顺序不同,有的特征先使用,有的特征后使用。由于每个特征的分类能力是不一样的,所以有理由应该最先使用分类能力强的特征。比如对于男女性别分类问题,年龄是一个特征,鞋跟高度是一个特征,衣服颜色是一个特征。显然对于男女性别分类问题来说,年龄特征的分类能力比较弱,鞋跟高度特征分类能力则比较强,而衣服颜色特征则介于二者之间,所以应该首先选择鞋跟高度特征优先使用应该是一个不错的选择。
按照这样的思路,我们可以这样建立一个决策树:先选用一个对数据集分类能力最强的特征,按照该特征的取值将数据集划分成几个子类。然后对于每个子类,再选用一个分类能力最强的特征,再将每个子类按照该特征的取值进行划分。注意,特征的分类能力与具体的数据集有关,所以这几个子类采用的不一定是同一个特征。这样一直划分下去,直到得到具体的类别为止,这样就完成了一个决策树的建立。当然这里只是给出了一个建立决策树的基本思路,还涉及到很多细节问题。最主要的问题就是如何根据数据集衡量一个特征的分类能力。下面我们介绍两种常用的建立决策树的方法——ID3算法和C4.5算法,不同方法之间最主要的区别就是如何评价特征的分类能力。
5.3.1决策树算法——ID3算法
艾博士:为了评价特征的分类能力,我们先看看如何评价一个数据集的混乱程度。以男女性别分类为例,如果一个数据集中有男性数据也有女性数据,则数据集是比较混乱的,如果一个数据集中只有男性数据或者只有女性数据,则数据集是纯净的。小明你觉得什么情况下这个数据集最混乱呢?
小明思考了一会儿回答到:男女数据各占一半时数据集最混乱吧?因为在这种情况下,如果没有任何其他信息,猜一个样本数据是男性数据还是女性数据的概率是50%,具有最大的不确定性。如果有些类别的数据多,有些类别的数据少,比如说男性数据占70%,女性数据占30%,则在这种情况下,当没有其他可用信息时,让我猜一个样本数据是男性数据还是女性数据,我肯定会猜测是男性数据,因为猜对的概率为70%。所以对于一个男性数据占70%、女性数据占30%的数据集,就不是那么混乱。
艾博士:所以说,一个数据集的混乱程度与其各个类别的占比,也就是概率有关。为此我们可以引用熵的概念,用熵的大小评价一个数据集的混乱程度。
小明:什么是熵呢?
艾博士:熵是度量数据集混乱程度的一种方法,通过数据集中各个类别数据的概率可以计算出该数据集的熵。
假设数据集由n个类别组成,每个类别的概率为Pi ,则该数据集D的熵H(D)由下式给出:
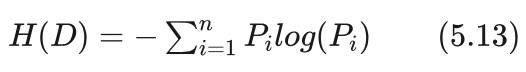
其中log为以2为底的对数运算。概率 Pi 由数据集计算得到: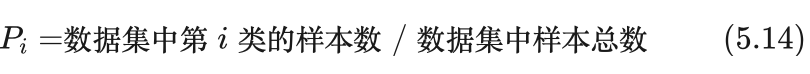
由于概率 Pi 都是大于等于0小于等于1的,所以取对数后 log(Pi) 是小于等于0的,也就是或者为0,或者为负数。这样由式(5.13)可以得到熵一定是大于等于0的。
小明有些疑惑地问到:概率 Pi 是有可能等于0的,而0的对数是负无穷,这种情况下如何计算熵呢?
艾博士解释说:在计算熵时,对于概率 Pi 等于0的情况,我们约定Pilog(Pi) 的值为0。
小明:这样约定就没有问题了。
下面我们举一个计算熵的例子。比如对于男女性别数据集,当男女数据各占一半时,类别为男性的概率和类别为女性的概率均为0.5,所以这种情况下该数据集的熵为:
H(D)=-(男性概率∙log(男性概率)+女性概率∙log(女性概率))
=-(0.5∙log(0.5)+0.5∙log(0.5) )
=-(0.5∙(-1)+0.5∙(-1))
=1
当男性数据为70%、女性数据为30%时,类别为男性的概率为0.7,类别为女性的概率为0.3,所以这种情况下该数据集的熵为:
H(D)=-(男性概率∙log(男性概率)+女性概率∙log(女性概率))
=-(0.7∙log(0.7)+0.3∙log(0.3) )
=-(0.7∙(-0.5146)+0.3∙(-1.7370))
=0.8813
小明:这两个例子确实说明了熵的大小可以反映数据集的混乱程度,熵值越大说明数据集越混乱。这与特征的分类能力有什么关系呢?
艾博士:如果按照特征的取值,将数据集划分成几个子数据集,这些子数据集的熵变小了,就说明采用这个特征后数据集比之前变得更纯净了。使用特征前后数据集熵的下降程度,是否就可以评价特征的分类能力呢?
小明:这是一个巧妙的想法,熵的下降程度越大,说明使用特征后的数据集越纯净,特征的分类能力也就越强。如果使用特征之后划分得到的几个子数据集是完全纯净的,也就是每个子集都是同一个类别的样本数据,则这种情况下熵的下降程度最大,也是我们希望得到的分类结果。
艾博士:但是这时又遇到了问题,采用特征后将数据集划分了几个子数据集,多个子数据集的熵怎么计算呢?
小明:是啊,我又把问题想简单了。
艾博士:这时我们要引用条件熵的概念,也就是按照特征A的取值将数据集D划分成了几个子数据集,综合计算这几个子数据集的熵,称作条件熵,表示为H(D|A)。
假设数据集为D,所使用的特征为A,共有n个取值,按照A的取值将数据集D划分成n个子数据集 ,则条件熵H(D|A)为子数据集的熵按照每个子数据集占数据集的比例的加权和。即:
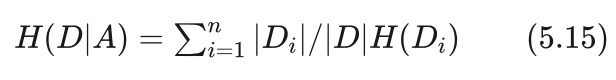
其中 |Di| 表示第i个子数据集 Di 的样本数,|Di| / |D|表示数据集D的样本数, 就是第i个子数据集 Di 占数据集D的比例, H(Di) 是第i个子数据集 Di 的熵,同样按照式(5.13)计算,只是数据采用第i个子数据集 Di 中的样本。
小明:我明白了,条件熵就相当于是每个子数据集熵的加权平均值,权重为每个子数据集占数据集的比例。
艾博士接着讲到:使用特征A前后数据集熵的下降程度我们称之为信息增益,用g(D,A)表示,由下式给出:
g(D,A)=H(D)-H(D│A) (5.16)
用信息增益就可以对特征的分类能力进行评价了,信息增益越大的特征,说明该特征的分类能力越强。
小明:我明白了。由式(5.16)可以看出,信息增益最大为H(D),此时条件熵H(D │ A)为0,说明特征A完全可以将数据集D划分成几个纯净的子数据集,每个子数据集中的样本都是相同的类别。信息增益最小为0,说明特征A使用前后数据集的熵没有变化,特征A没有任何分类能力。
接着小明又问到:这样的话,是不是先按照信息增益对特征排一个序,然后按照顺序使用特征,建立决策树就可以了?
艾博士:小明你又把问题想简单了,特征的分类能力是与具体的数据集有关的,在一个数据集下分类能力强的特征,换一个数据集分类能力可能就没有那么强了。比如说,我们前面讨论过,对于男女性别分类来说,鞋跟高度可能是一个分类能力比较强的特征,这是从一般情况说的,如果一个数据集中全是穿平底鞋的,那么鞋跟高度就没有任何分类能力了。
小明:从式(5.16)也确实可以看出信息增益是与具体的数据集有关。
艾博士:所以说建立决策树时,先用全部数据集D按照信息增益选择一个特征A,按照特征A的取值将数据集D划分成D1 、D2、...、Dn 等n个子数据集,对这n个子数据集再分别计算每个特征的信息增益,每个子数据集Di分别选出对应的信息增益最大的特征 Ai ,这几个特征可能是相同的,也可能是不同的,完全由具体的子数据集决定。
讲到这里艾博士强调说:这种按照信息增益选择特征建立决策树的方法,称作ID3算法。
小明:为什么称作ID3算法呢?
艾博士:ID3算法的全称是Iterative Dichotomiser 3,直译过来就是“第三代迭代二分器”的意思。这里“迭代”的意思是指,对于每个子数据集,包括子数据集的子数据集…,都采用相同的方法选择特征,一层层地逐渐加深建立决策树。而“二分器”指的是每个节点(对应决策树建立过程中的某个数据集)都可以划分成两部分。但是实际上ID3算法建立的决策树不仅仅是“二分”的,也可以是“多分”的,之所以叫做“二分器”可能与早期的决策树形式有关,逐渐改进之后也允许“多分”了。
小明:原来是这样的。
艾博士:下面我们首先给出ID3算法的具体描述,然后再详细讲解其建立决策树的过程。简单地说,ID3算法就是采用上面提到的建立决策树的思想,按照信息增益选择特征,按照特征的取值将数据集逐步划分成小的子数据集,采用递归的思想建立决策树。
ID3算法
输入:训练集D,特征集A,阈值ε
输出:决策树T
1,如果D中所有样本均属于同一类别 Ck ,则T为单节点树,将Ck 作为该节点的类别标志,返回T
2,如果A为空,则T为单节点树,将D中样本最多的类 Ck 作为该节点的类别标志,返回T
3,否则计算A中各特征对D的信息增益,选择信息增益最大的特征 Ag
4,如果 Ag 的信息增益小于阈值ε,则将T视作单节点树,将D中样本最多的类 Ck 作为该节点的类别标记,返回T
5,否则按照Ag 的每个可能取值 ai ,将D划分为n个子数据集 Di ,作为D的子节点
6,对于D的每个子节点 Di ,如果 Di 为空,则视 Ti 为单节点树将 Di 的父节点D中样本最多的类作为 的类别标记
7,否则以 Di 作为训练集,以 A-Ag为特征集,递归地调用算法的1到6步,得到子决策树 Ti ,返回 Ti
艾博士:下面我们就具体解释一下ID3算法建立决策树的过程。
首先,算法的输入包括:一个用于训练的数据集。一个特征集,特征集包含了所有可以使用的特征。一个大于0的阈值ε,当信息增益小于该阈值时,认为信息增益为0,特征不具有任何分类能力。
算法的输出就是一个决策树。由于算法是递归实现的,所以算法输出的也可能只是决策树的某个叶节点,或者是一个子决策树。比如由某个子数据集建立的子决策树。
算法的前几步为处理几种特殊情况。第一步判断数据集D是否都是同一个类别的样本,如果都是同一个类别,则说明该数据集不需要再分类了,应该成为决策树的一个叶节点,按照样本的类别标记该节点的类别。
小明有些不解地问到:为什么会出现数据集D都是同一个类别的情况呢?收集数据集时不是要尽可能各种类别都有吗?
艾博士:收集数据集时确实如小明所说,需要各个类别都有。ID3算法是按照选择的特征逐渐划分数据集,所以这里的数据集D不一定是最原始的训练用数据集,而是算法按照特征对数据集进行划分过程中得到的某个小数据集,这种情况下数据集D很可能就是单一类别的样本,而且随着决策树的建立,当用了多个特征对数据集划分之后,我们也希望最后得到的小数据集是由单一样本组成的,这样才说明这些特征具有比较好的分类效果。比如对于男女性别分类问题,如果采用了鞋跟高度特征之后,取值高跟的划分为一个子数据集,取值平底的划分为另一个子数据集,如果穿高跟鞋的刚好都是女性,而穿平底鞋的刚好都是男性,则两个子数据集都是同一个类别的样本数据。
小明:我明白了,由于按照特征的取值对数据进行反复划分,最后得到的数据集就会出现单一类别的情况,而这也正是我们所希望的结果。
艾博士继续讲解说:ID3算法的第二步,如果特征集A为空,这时即便数据集D中的样本不是单一类别的,由于已经没有特征可用了,也不能继续按照特征的取值对数据集D做进一步划分了,这时只能将数据集D当作决策树的一个叶节点,其类别标记为D中类别最多样本的类别。比如如果这时D中的样本有8个男性、3个女性,男性样本多于女性的样本,则将该节点标记为男性类别。
小明:为什么会出现特征集为空的情况呢?
艾博士:假设我们用特征 Ag 的取值将数据集D划分为n个子数据集 Di ,然后再用信息增益最大的特征 Ai 分别对子数据集 Di 做划分。对于子数据集 Di 来说,是用特征 Ag 的取值划分得到的,那么再对子数据集 Di 做划分时,特征 Ag 已经没有意义,需要从特征集中删除特征 Ag ,从其他特征中选择一个信息增益最大的特征。同样,在对数据集 Di 的子数据集做划分时,也要删除所选择的Ai 这个特征。这样的话,随着按照特征取值对数据集做划分的进行,可用的特征会越来越少,最终就可能出现特征集为空的情况。
小明:这跟随着数据集逐步划分成小数据集,最后会出现单一类别的数据集是同一个道理。
艾博士:但是这时也要注意,避免初学者容易犯的错误。我们通过一个具体例子来说明吧。
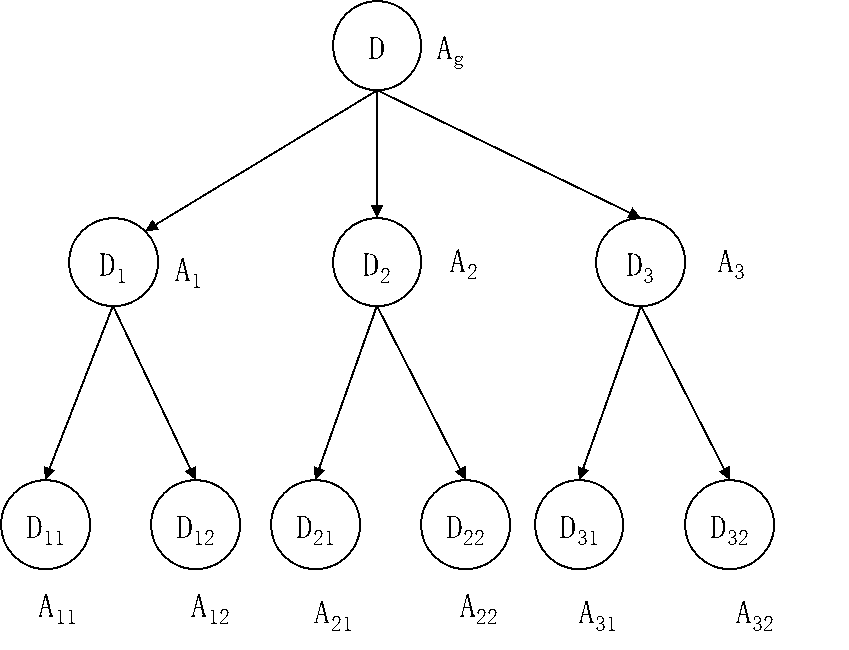
图5.9 决策树建立示意图
如图5.9所示,数据集D由特征 Ag(假定 有三个取值)划分为 D1、D2、D3 三个子数据集,这样接下来在对D1、 D2、D3 三个子数据集做划分时,就不能再用特征 Ag 了,因为这三个数据集就是根据 Ag 的取值划分的,再用也没有任何意义。然后 D1 被特征A1 划分为D11 和D12 、D2 被特征 A2 划分为 D21 和 D22 、 D3 被特征 A3 划分为 D31 和 D32。A1 、A2、A3 这三个特征可能相同也可能不相同,三个特征之间没有任何关联,完全根据 D1、D2、D3 所包含的样本,依据信息增益进行选择。接下来在对 D11 和 D12 两个数据集做划分时,Ag 和 A1两个特征就不能再用了,因为这两个数据集是使用了Ag 和 A1 两个特征后得到的数据集,但是特征 A2 和 A3 还是可以用的,除非这两个特征与 Ag 或者A1 相同。同样的,在对 D21 和D22 两个数据集做划分时,Ag 和A2 两个特征不能用了,特征 A1 和 A3 是可以用的,除非这两个特征与Ag 或者 A2 相同。其他的也都类似。
小明:这个例子很说明问题,并不是用过的特征都不能用了,只是与当前数据集有关系的特征不能再使用。比如在这个例子中,D11 和 D12 两个数据集与特征 Ag 和 A1 有关系,是采用这两个特征后得到的数据集,所以 D11 和 D12 两个数据集不能再用特征 Ag 和 A1 ,而特征 A2 和 A3 与 D11 和 D12 没有关系,所以还可以使用。
艾博士称赞到:小明总结的很好。
ID3算法的第三步,特征集A中的每个特征计算对数据集D的信息增益,从中选择一个信息增益最大的特征 Ag 。这一步就是计算信息增益的过程,前面介绍过具体方法,这里不再重复。
ID3算法的第四步,如果最大的信息增益 Ag 小于给定的阈值,则认为该特征已经没有什么分类能力了,基本等同于算法第二步的特征集A为空的情况,按照同样的办法处理,不再赘述。
ID3算法的第五步,按照特征 Ag 的n个取值a1 、a2、...、an ,将数据集D划分为n个子数据集 Di ,每个子数据集Di 作为数据集D的子节点连接。如下图5.10所示。
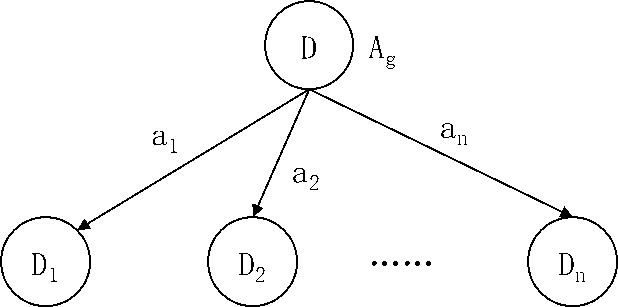
图5.10 按照Ag的n个取值对D做划分
对于ID3算法的第六步,我们先暂时放一放,最后再做解释。
ID3算法的第七步,接下来就是以算法第五步产生的每个子数据集 分别作为训练集,递归地调用ID3算法的第一到第六步,为每个子数据集建立一个子决策树 Ti 。由于这几个子数据集是用特征 Ag 的取值划分得到的,所以在建立子决策树 Ti 时,要将特征 Ag 从特征集A中去除,即以 A-{Ag} 为特征集。
最后我们再返回来说说ID3算法的第六步,这一步是对可能遇到的特殊情况进行处理。当按照特征的取值对数据集划分时,可能会遇到某个子数据集为空的情况,也就是该子数据集中一个样本也没有。比如在图5.10中,如果数据集D中没有任何样本的Ag 特征取值为 a2 ,则子数据集 D2 就为空。这种情况下,我们也要为子数据集 D2 标记一个类别,以便在实际使用时,万一有样本落入这个节点时获得一个分类结果。
小明有些不解地问到:这个节点为空说明没有任何训练样本落入这个节点,怎么对它标注类别呢?从算法中看类别标记都是根据样本情况标记的。
艾博士:确实存在小明所说的情况,所以要特殊处理。在这种情况下,我们就是猜测一个类别作为这个叶节点的分类标记。
小明问到:怎么猜测呢?
艾博士:在ID3算法中是这样处理的:以其父节点数据集D中样本数最多的类别作为该叶节点的类别标记。比如D中男性样本多于女性样本,则该节点就标记为男性。
小明:我明白ID3算法的处理思路了,就是既然这个节点为空,不能确定其类别标记,就按照其父节点的样本情况,猜测一个分类标记。万一在实际使用中有样本落入该节点时,就以猜测的分类标记作为输出。
艾博士:讲了这么多,我们还是举例说明如何使用ID3算法建立一个决策树吧?我们采用表5.1给出的男女性别数据作为训练集,建立一个用于男女性别分类的决策树。为了方便计算,我们再次复制表5.1如表5.3所示。
表5.3 男女性别样本数据表
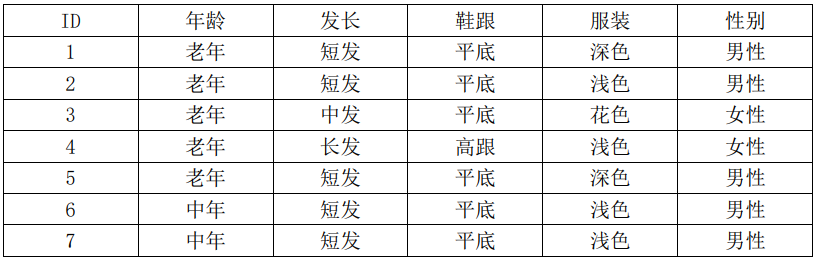
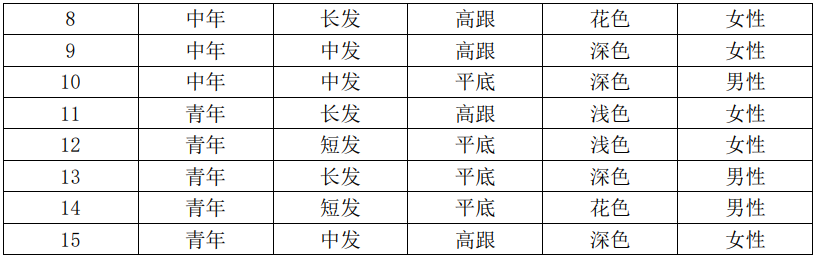
首先开始的时候数据集D就是表5.3所示的这个表,先计算数据集D的熵:
数据集D共有15个样本,其中男性样本有8个,女性样本有7个,则男性、女性的概率分别为:
P(男性)=8/15=0.5333
P(女性)=7/15=0.4667
根据式(5.13)有D的熵为:

接下来根据式(5.15)计算每个特征的条件熵:
对于年龄特征,共有老年、中年和青年三个取值,每个取值都有5个样本。当取值为老年时,5个样本中有3个男性、2个女性,我们得到这个子数据集下男性、女性的概率分别为:
P(男性)=3/5=0.6
P(女性)=2/5=0.4
所以对于取值老年时子数据集的熵,我们用H(老年)表示:
H(老年)=-(P(男性)∙log(P(男性))+P(女性)∙log(P(女性)) )
=-(0.6∙log(0.6)+0.4∙log(0.4) )
=0.9710
相应地,我们可以计算出取值中年、取值青年时子数据集的熵,下面我们直接给出计算结果:
H(中年)=0.9710
H(青年)=0.9710
小明看着艾博士的计算结果有些疑惑地问到:怎么三个子数据集的熵都是0.9710?
艾博士回答说:是的,恰好都是这个结果。因为对于年龄特征,老年、中年和青年三个取值都是各有5个样本,而且三个取值中不是3个男性2个女性,就是2个男性3个女性,这两种情况熵都是一样的。
小明:明白了。
艾博士又继续讲解了起来:根据式(5.15)有特征年龄的条件熵为:

由此我们得到年龄的信息增益为:
g(D,年龄)=H(D)-H(D│年龄)
=0.9968-0.9710
=0.0258
对于发长特征,共有短发、中发和长发三个取值,其中短发有7个样本,中发和短发各有4个样本。当取值为短发时,7个样本中有6个男性、1个女性,我们得到这个子数据集下男性、女性的概率分别为:
P(男性)=6/7=0.8571
P(女性)=1/7=0.1429
所以对于取值短发时子数据集的熵,我们用H(短发)表示:
H(短发)=-(P(男性)∙log(P(男性))+P(女性)∙log(P(女性)) )
=-(0.8571∙log(0.8571)+0.1429∙log(0.1429) )
=0.5917
相应地,我们可以计算出取值中发和长发时子数据集的熵,下面我们直接给出计算结果:
H(中发)=0.8113
H(长发)=0.8113
根据式(5.15)有发长特征的条件熵为:

由此我们得到发长的信息增益为:
g(D,发长)=H(D)-H(D│发长)
=0.9968-0.7088
=0.2880
对于鞋跟特征,共有高跟和平底两个取值,其中高跟有5个样本,平底有10个样本。当取值为高跟时,5个样本均为女性,没有男性样本。我们得到这个子数据集下男性、女性的概率分别为:
P(男性)=0/5=0
P(女性)=5/5=1
所以对于取值高跟时子数据集的熵,我们用H(高跟)表示:
H(高跟)=-(P(男性)∙log(P(男性))+P(女性)∙log(P(女性)) )
=-(0∙log(0)+1∙log(1) )
=0
讲到这里艾博士问小明:这里就遇到了对0取对数的问题,由于0的对数是负无穷大,还记得怎么处理这个问题吗?
小明回答说:记得呢,前面我问过这个问题,对于概率等于0的情况,按照0∙log(0)等于0处理。
艾博士:小明回答得非常正确!
艾博士继续讲到:相应地,我们可以计算出取值平底时子数据集的熵,下面我们直接给出计算结果:
H(平底)=0.7219

由此我们得到鞋跟特征的信息增益为:
g(D,鞋跟)=H(D)-H(D│鞋跟)
=0.9968-0.4813
=0.5155
对于服装特征,共有深色、浅色和花色三个取值,其中深色有6个样本,浅色有6个样本,花色有3个样本。当取值为深色时,6个样本中有4个男性、2个女性,我们得到这个子数据集下男性、女性的概率分别为:
P(男性)=4/6=0.6667
P(女性)=2/6=0.3333
所以对于取值深色时子数据集的熵,我们用H(深色)表示:
H(深色)=-(P(男性)∙log(P(男性))+P(女性)∙log(P(女性)) )
=-(0.6667∙log(0.6667)+0.3333∙log(0.3333) )
=0.9183
相应地,我们可以计算出取值浅色和花色时子数据集的熵,下面我们直接给出计算结果:
H(浅色)=1
H(花色)=0.9183
根据式(5.15)有服装特征的条件熵为:

由此我们得到服装的信息增益为:
g(D,服装)=H(D)-H(D│服装)
=0.9968-0.9510
=0.0458
比较年龄、发长、鞋跟和服装四个特征的信息增益,鞋跟特征的信息增益最大为0.5155,所以对于决策树的根节点采用鞋跟特征对数据集D做划分,按照特征的高跟和平底两个取值,得到两个子数据集D1和D2,如果我们用样本ID的集合表示子数据集,则有:
D1=4,8,9,11,15
D2=1,2,3,5,6,7,10,12,13,14
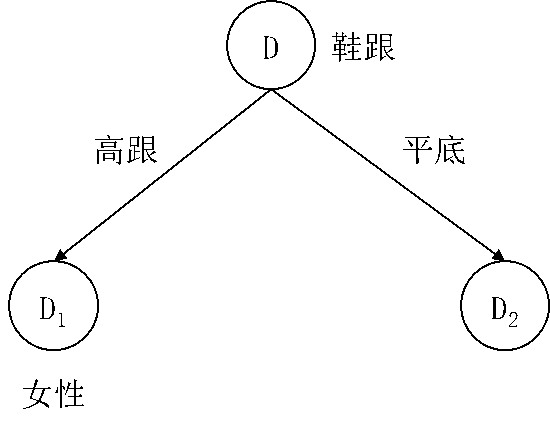
图5.11 使用鞋跟特征后得到的决策树局部
由于子数据集 D1 中样本的类别均为女性,所以 D1 成为决策树的一个叶节点,其类别标记为女性。
到此我们得到决策树的一个局部如图5.11所示。
由于子数据集 D1 是单一类别的样本集,不需要再处理,接下来对 D2 再次应用ID3算法。
首先计算数据集D2 的熵。 D2 中共有10个样本{1,2,3,5,6,7,10,12,13,14},数字表示样本的ID,其中8个男性样本2个女性样本,所以男性、女性的概率分别为:

下面我们计算每个特征的信息增益。在计算信息增益时,要将鞋跟特征从特征集中删除,我们再一次计算年龄、发长和服装这三个特征的信息增益。
小明:年龄、发长和服装这三个特征的信息增益前面已经计算过l,为什么不拿过来直接用呢?
艾博士:前面确实计算过这三个特征的信息增益,但是是对数据集D计算的,而现在是对数据集 D2 计算。我们曾经说过,信息增益是与数据集相关的,不同的数据集计算得到的信息增益可能不一样。
小明:对啊,您前面曾经讲过这个问题,我给忘记了。
艾博士:好的,下面我们就分别计算这三个特征在数据集 D2 上的信息增益。
对于年龄特征,共有老年、中年和青年三个取值,其中取值老年的样本有4个,取值中年和青年的样本各有3个。
当取值为老年时,4个样本中有3个男性、1个女性,我们得到这个子数据集下男性、女性的概率分别为:
P(男性)=3/4=0.75
P(女性)=1/4=0.25
所以对于取值老年时子数据集的熵,我们用H(老年)表示:
H(老年)=-(P(男性)∙log(P(男性))+P(女性)∙log(P(女性)) )
=-(0.75∙log(0.75)+0.25∙log(0.25) )
=0.8113
相应地,我们可以计算出取值中年、取值青年时子数据集的熵,下面我们直接给出计算结果:
H(中年)=0
H(青年)=0.9183
根据式(5.15)有数据集 关于年龄特征的条件熵为:
由此我们得到年龄特征在数据集D2上的信息增益为:
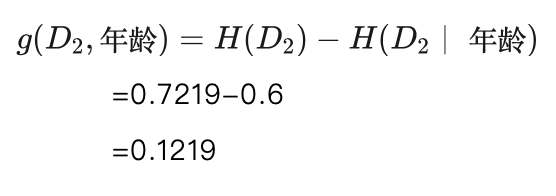
对于发长特征,共有短发、中法和长发三个取值,其中取值短发的样本有7个,取值中发的样本有2个,取值长发的样本有1个。
当取值为短发时,7个样本中有6个男性、1个女性,我们得到这个子数据集下男性、女性的概率分别为:
P(男性)=6/7=0.8571
P(女性)=1/7=0.1429
所以对于取值短发时子数据集的熵,我们用H(短发)表示:
H(短发)=-(P(男性)∙log(P(男性))+P(女性)∙log(P(女性)) )
=-(0.8571∙log(0.8571)+0.1429∙log(0.1429) )
=0.5917
相应地,我们可以计算出取值中发、取值长发时子数据集的熵,下面我们直接给出计算结果:
H(中发)=1
H(长发)=0
根据式(5.15)有数据集D2关于发长特征的条件熵为:

由此我们得到发长特征在数据集D2上的信息增益为:
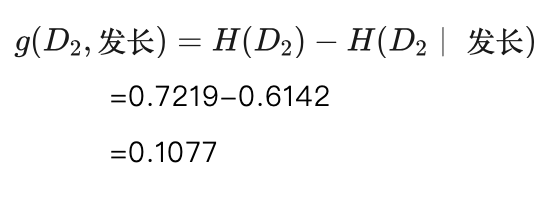
对于服装特征,共有深色、浅色和花色三个取值,其中取值深色的样本有4个,取值浅色的样本有4个,取值花色的样本有2个。
当取值为深色时,4个样本均为男性,我们得到这个子数据集下男性、女性的概率分别为:
P(男性)=4/4=1
P(女性)=0/4=0
所以对于取值深色时子数据集的熵,我们用H(深色)表示:
H(深色)=-(P(男性)∙log(P(男性))+P(女性)∙log(P(女性)) )
=-(1∙log(1)+0∙log(0) )
=0
相应地,我们可以计算出取值浅色、花色时子数据集的熵,下面我们直接给出计算结果:
H(浅色)=0.8113
H(花色)=1
根据式(5.15)有数据集 关于服装特征的条件熵为:

由此我们得到服装特征在数据集 D2 上的信息增益为:
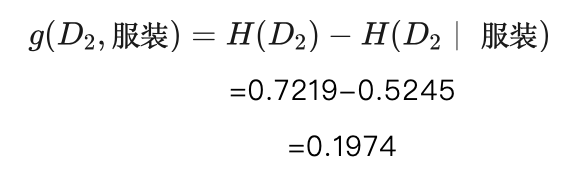
比较年龄、发长和服装三个特征对数据集 D2 的信息增益,服装特征的信息增益最大为0.1974,所以对于决策树的节点 d2 采用服装特征对其做划分,按照服装特征的深色、浅色和花色三个取值,得到数据集D2 的三个子数据集D21 、D22 和 D23 ,如果用样本ID的集合表示这三个子数据集,则有:
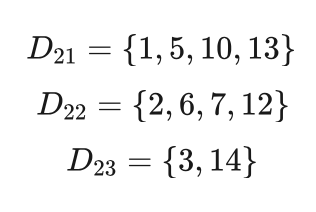
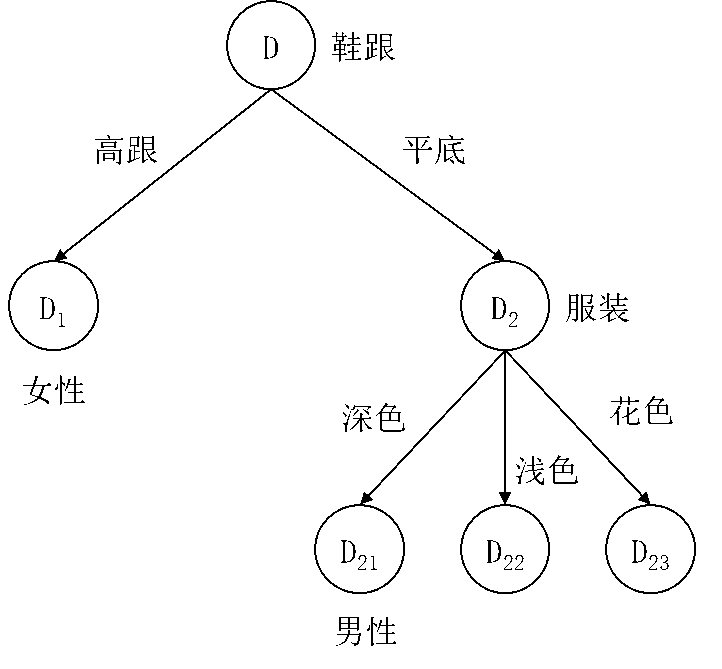
图5.12 决策树中间结果
由于子数据集 D21 中样本的类别均为男性,所以 D21 成为决策树的一个叶节点,其类别标记为男性。
到此为止我们得到如图5.12所示的决策树,其中D22 和 D23 两个子数据集还需要进一步处理。
对于 D22 和 D23 两个子数据集均还有年龄和发长两个特征可用。经计算,年龄特征和发长特征两个特征对数据集 D22 的信息增益分别为0.8113、0.4868,年龄特征的信息增益最大,按照其三个取值老年、中年和青年将数据集 D22 划分为 D221、D222、D223 三个子数据集,拥有的样本分别为:
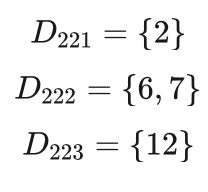
其中 D221 中的样本为男性,该节点标注为男性, D222 中的样本为男性,节点被标注为男性,D223 中的样本为女性,节点被标注为女性。
经计算,年龄特征和发长特征这两个特征对数据集 D23 的信息增益都是1,我们随机选择一个作为信息增益最大的特征,比如选择发长特征,这样数据集 D23 按照该特征的短发、中发和长发三个取值,被划分为 D231、D232、D233 三个子数据集,拥有的样本分别为:
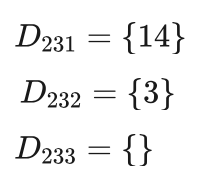
其中D231 中的样本为男性,该节点标注为男性, D232 中的样本为女性,节点标注为女性。 D233 中没有样本,小明你说说这种情况下应该如何处理?D233 应该如何标注?
小明:刚刚您讲过,对于没有样本的节点,类别按照其父节点中样本最多的类别进行标注。对于 D233 来说,其父节点为 D23 ,但是 D23 中只有ID为3和14两个样本,这两个样本又分别为男性和女性,这种情况如何处理我就不知道了。
艾博士:这确实是一个非常特殊的情况,主要是我们的例题样本过少造成的。这种情况下我们可以继续向上看,根据D23 的父节点 D2 中的样本情况做标注。在 D2 中共有8个男性样本,2个女性样本,所以按照样本多的类别, D233可以标记为男性。
小明:我明白怎么处理了。
艾博士:至此我们采用ID3算法就完成了决策树的建立,建立的决策树如图5.13所示。建立决策树属于训练过程,在实际使用时,对于一个待分类样本,依据决策树,按照样本的特征取值就可以实现分类了。比如对于一个“年龄为青年、鞋跟为平底、发长为中发、服装为浅色”的样本,应该标记为哪个类别呢?
小明回答说:按照图5.13所示的决策树,该样本应该属于女性。因为按照决策树,从根节点开始,根据鞋跟为平底达到 D2 节点,再依据服装为浅色,到达 D22 节点,最后根据年龄为青年,到达 D223 节点,而该节点的类别标记为女性,所以有样本“年龄为青年、鞋跟为平底、发长为中发、服装为浅色”被分类为女性。
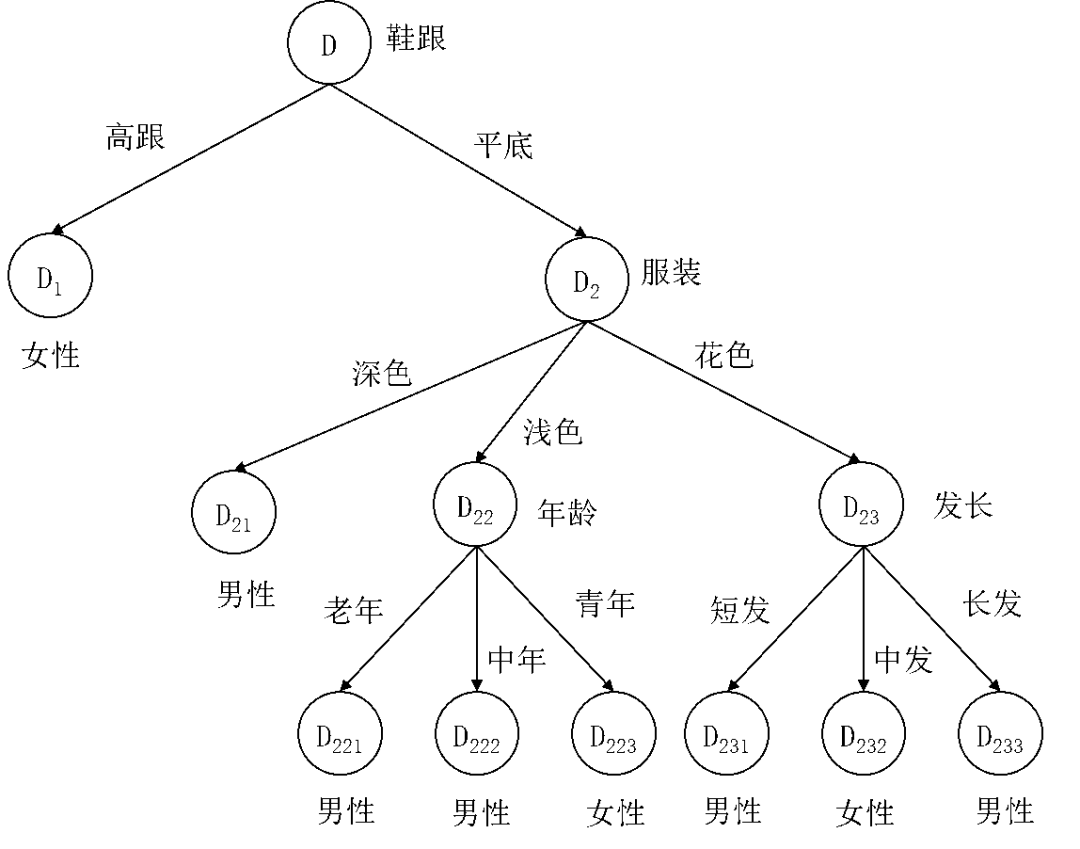
图5.13 采用ID3算法建立的决策树
艾博士:对,决策树就是这样对待分类样本进行分类的。
未完待续

