第五篇 统计学习方法是如何实现分类与聚类的(二)
清华大学计算机系 马少平
第二节:朴素贝叶斯方法
艾博士:朴素贝叶斯方法是一种基于概率的分类方法,其基本思想是,对于一个以若干特征表示的待分类样本,依次计算样本属于每个类别的概率,其中所属概率最大的类别作为分类结果输出。
为了叙述方便,我们给出如下的符号表示:设共有K个类别,分别用y1,y2,...,yk 表示。每个样本具有N个特征,分别为A1,A2,...,An ,每个特征 Ai 又有 Si 个可能的取值,分别为 ai1,ai2,...,aisi 。
小明:这些看起来有些抽象,您结合例子具体说明一下吧。
艾博士:好的,我们还是以前面说过的男女性别分类的例子加以说明。在该例子中,共有男性和女性两个类别,所以类别数K为2,我们可以用 y1 表示男性,用 y2 表示女性。每个样本有“年龄”、“发长”、“鞋跟”和“服装”共四种特征,我们可以用 A1 表示“年龄”,A2 表示“发长”,A3 表示“鞋跟”, A4 表示“服装”。年龄特征 A1 可以有“老年”、“中年”和“青年”三种取值,则特征 A1 的取值个数 S1 为3,分别可以用 a11表示老年,用a12 表示中年,用 a13 表示青年。同样的,发长特征 A2 可以有“长发”、“中发”和“短发”三种取值,则特征A2 的取值个数 S2为3,分别可以用 a21 表示长发,用 a22 表示中发,用 a23 表示短发。以此类推,对于特征“鞋跟”和“服装”也可以用类似的表示方法进行表示,我们就不一一说明了。
小明:有了这几个例子就清楚各个符号的具体含义了。
艾博士:对于待分类样本我们用x表示:
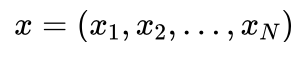
其中 xi 为待分类样本的第i个特征 Ai 的取值。
比如:x=(青年,中发,平底,花色),表示的是一个年龄特征为青年,发长特征为中发,鞋跟特征为平底,服装特征为花色的样本。
我们的目的就是计算给定的待分类样本x属于某个类别 的概率 ,然后将x分类到概率值最大的类别中。
小明:这个概率怎么计算呢?
艾博士:一般来说这个概率并不是太好计算,需要转换一下。小明你还记得我们在第三篇求解拼音输入法问题时提到过的贝叶斯公式吗?
小明回想了一会儿回答说:我印象中贝叶斯公式是这样的:
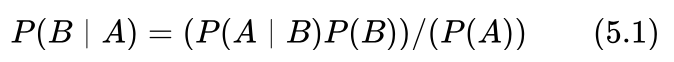
艾博士:对,就是这个贝叶斯公式。我们看看这个贝叶斯公式是否可以帮助到我们。
假设待分类样本的出现表示事件A,而属于类别 表示事件B,则根据贝叶斯公式我们有:
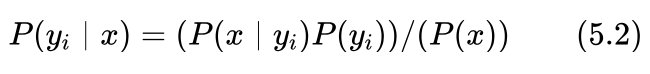
上式中,P(yi) 表示类别 出现的概率,P(x|yi)表示在类别 x=(x1,x2,...,xn) 中出现特征取值为 的概率。
我们的目的就是通过贝叶斯公式,计算待分类样本x在每个类别中的概率,然后以取得最大概率的类别作为分类结果。
由于待分类样本是给定的,所以对于这个问题来说,P(x)是固定的,所以求概率 P(yi | x)最大与求 P(x | yi)P(yi)最大是等价的。因为我们并不关心属于哪个类别的概率具体是多少,而只关心属于哪个类别的概率最大。
因此问题转化为了如何计算下式在哪个类别 yi 下最大问题:
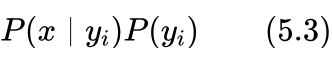
这是两个概率的乘积,如果分别可以计算出两个概率值 P(x | yi)、P(yi) ,那么这个问题也就解决了。这样的分类方法称为贝叶斯方法。
讲到这里艾博士询问小明:你觉得这两个概率值怎么计算呢?
小明:概率一般都是根据数据统计计算。如果有了训练集,通过训练集是否就可以计算出这两个概率?
我计算一下试试看。比如还是前面的男女性别分类的例子,为了计算方便,我们将表5.1复制如下如表5.2所示:
表5.2 男女性别样本数据表
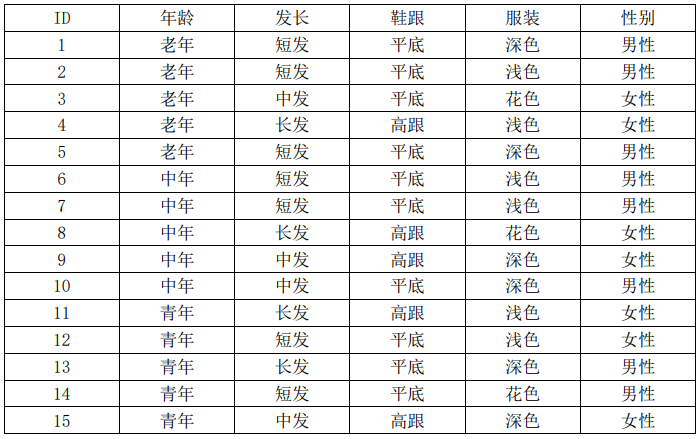
我觉得类别概率 P(yi) 比较容易计算,属于类别yi 的样本数除以总样本数就可以了,即:

表5.2中共15个样本,其中8个类别为男性,7个类别为女性。所以有:

概率 P(x | yi)体现的是类别 yi 中具有x特征的概率,与具体的待分类样本有关,前面给的待分类样本的例子x=(青年,中发,平底,花色)。我发现数据集中没有一个这样的样本,所以按照该数据集计算的话,得到的概率为0。这就出现问题了,因为无论是男性类别还是女性类别,式(5.3)的计算结果都为0,无法判断属于哪个类别的概率更大。是不是训练集数据量太少了?
艾博士:对于我们这个例题来说,数据集确实有点小,但是小明你提到的问题本质上并不是数据集大小的问题,而是组合爆炸问题。
小明:为什么会有组合爆炸问题呢?
艾博士:小明你看,一个样本由多个特征组成,而每个特征又有多个取值,这样每个特征的每一个可能取值都会组成一个样本,再考虑不同的类别,都需要计算其概率值,其总数是每个特征取值数的乘积再乘以类别数,当类别数、特征数和特征的取值数比较多时,就出现了组合爆炸问题。以这个例题为例,特征包含了年龄、发长、鞋跟和服装等四种特征,而年龄、发长和服装三个特征均有三个取值,鞋跟特征有两个取值,类别分为男性和女性两个类别,这样可能的组合数就是3×3×3×2×2=108种。由于这个例题中特征数、特征的取值数和类别数都比较小,组合爆炸问题还不太明显,如果类别数、特征数和特征可能的取值数比较多时,需要估计的概率值将会呈指数增加,从而造成组合爆炸。这样,需要非常多的样本才有可能比较准确地估计每种情况下的概率值,而对于实际问题来说,很难做到如此全面地采集数据。
小明:那么如何解决这个问题呢?
艾博士:为解决这个问题,我们可以假设各特征间是独立的。在独立性假设下,特征每个取值的概率可以单独估计,不存在组合问题,也就消除了组合爆炸问题。在这样的假设下,给定类别y_i时某个特征组合的联合概率等于该类别下各个特征单独取值概率的乘积。即:
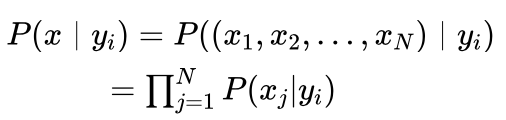
其中 P(xj | yi) 为类别为 yi 时,第j个特征 Aj 取值为xj 的概率,N为特征个数。
在引入独立性假设后,式(5.3)可以写为:

这样分类问题就变成了求式(5.5)最大时所对应的类别问题。这种引入了独立性假设后的贝叶斯分类方法称作朴素贝叶斯方法。
小明:这样处理会带来哪些好处呢?
艾博士:这样对于特征每个取值的概率就可以单独计算了,不需要考虑与其他特征的组合情况,减少了对训练集数据量的需求,计算起来更加简单。下面我们给出具体的计算方法。
在给定类别 yi 的情况下,特征 Ak 取值为akj 的概率 P(akj | yi) 可以通过训练集计算得到:

回到我们的例题,由于x=(青年,中发,平底,花色),就是要分别计算以下几个概率的乘积:
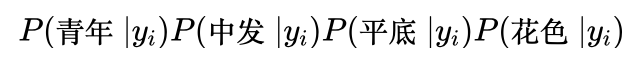
小明你再试试,看是否可以根据数据集计算出这几个概率来?
小明对照这表5.2所示的数据认真计算起来:
当类别 yi 为男性时共有8个样本,其中2个样本年龄为青年,所以有:
P(青年│男性)=2/8=0.25
其中1个样本发长为中发,所以有:
P(中发│男性)=1/8=0.125
其中8个样本鞋跟全部为平底,所以有:
P(平底│男性)=8/8=1
其中1个样本服装为花色,所以有:
P(花色│男性)=1/8=0.125
在加上我们前面已经计算过的:
P(男性)=8/15=0.5333
以上结果带入式(5.3)中,有:
P(x│男性)P(男性)=P(青年│男性)P(中发│男性)P(平底│男性)P(花色│男性)P(男性)
=0.25×0.125×1×0.125×0.5333
=0.002083 (5.7)
当类别 为女性时共有7个样本,其中3个样本年龄为青年,所以有:
P(青年│女性)=3/8=0.375
其中3个样本发长为中发,所以有:
P(中发│女性)=3/8=0.375
其中2个样本鞋跟为平底,所以有:
P(平底│女性)=2/8=0.25
其中2个样本服装为花色,所以有:
P(花色│女性)=2/8=0.25
在加上我们前面已经计算过的:
P(女性)=7/15=0.4667
以上结果带入式(5.3)中,有:
P(x│女性)P(女性)=P(青年│女性)P(中发│女性)P(平底│女性)P(花色│女性)P(女性)
=0.375×0.375×0.25×0.25×0.4667
=0.004102 (5.8)
看到小明计算完之后,艾博士说:根据你的计算结果,待分类样本x=(青年,中发,平底,花色)应该属于哪个类别?
小明对比了式(5.7)和(5.8)的计算结果后回答到:式(5.8)的计算结果大于式(5.7)的计算结果,说明待分类样本x=(青年,中发,平底,花色)属于女性的概率大于属于男性的概率,所以应该被分类为女性。
艾博士:小明你看,引入了独立性假设后这个问题是不是就简单多了?即便训练数据集不大的情况下,也可以计算了。
小明:引入了独立性假设后问题确实简单了不少,但是有些特征之间并不是完全独立的。比如年龄特征和鞋跟特征,对于老年人来说,由于行走不方便,自然穿高跟鞋的就少,二者是有一定的相关性的。在实际问题中,特征之间具有一定的相关性的情况肯定会更多,这样的话,朴素贝叶斯分类方法适用于求解实际问题吗?
艾博士解释说:正像小明所说,实际问题中特征之间一般会具有一定的相关性,并不完全满足独立性假设。一方面如果不引入独立性假设,参数量也就是需要估计的概率值太多,很难有足够的数据集支持这些参数的估计。另一方面,朴素贝叶斯分类方法在解决实际问题中的效果还是不错的。所以引入独立性假设也是不得已采用的一种简化手段,以便于真正将这种方法用于解决实际问题。
小明:在实际使用朴素贝叶斯方法的时候,每次都通过训练数据集计算概率值,会不会比较慢?
艾博士:实际使用时,一般是根据训练数据集事先计算好所有的概率值,存储起来,这个过程属于训练过程。在具体分类时直接调用所需要的概率值就可以了,这个过程属于分类过程。
另外,由于概率值一般都比较小,式(5.5)是多个概率值的连乘运算,当特征比较多时,连乘运算的结果会变得越乘越小,可能会出现计算结果下溢的情况发生,即当运算结果小于计算机所能表示的最小值之后,就被当作0处理了。为此一般通过取对数的方式将连乘运算转化为累加运算,即用下式代替式(5.5),二者取得最大值的类别y_i是一样的,不影响分类结果。
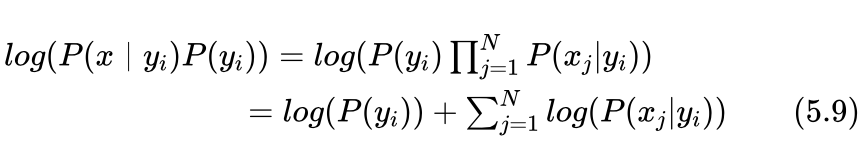
小明:艾博士,我又想到了一个问题。当用式(5.6)计算概率值时,是不是也会出现概率为0的情况?比如对于表5.2所示的数据集中,当类别为男性时鞋跟特征取值为高跟的数据一个也没有,这样就会导致概率P(高跟|男性)为0的情况出现。这种情况怎么处理呢?
艾博士:小明提出了一个很好的问题。在实际应用中,训练集再大也不可避免地出现某种情况下样本为0的情况发生,为此可以采用拉普拉斯平滑方法避免概率为0的情况发生。
小明:什么是拉普拉斯平滑方法呢?
艾博士:拉普拉斯平滑方法很简单,其基本思想是,假定每一种情况都至少出现一次,而无论数据集中是否出现过。也就是说,在用式(5.6)计算概率 P(akj | yi) 时,对于分子中的“类别 yi 的样本中特征 Ak 值为 akj 的样本数”进行计数时,采用在原有计数的基础上再加1的方法,防止出现0的情况。对于具有 Sk 个取值的特征 Ak 来说,在类别 yi 下其所有取值的概率和应该为1,即:
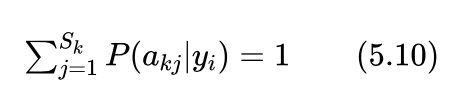
为此对式(5.6)的分母应该相应地增加 Sk 以满足概率和为1这一条件。这样在采用了拉普拉斯平滑后,式(5.6)就变成了下式:

这样就避免了出现概率等于0的情况发生。
小明问到:没有太想明白为什么在分母中要加上 呢?
艾博士:因为特征 Ak 具有 Sk 个取值,计数时每个取值的样本数都增加了一个,相当于多了 Sk个样本,这样在分母中就需要加上 Sk 。这样处理后才能满足式(5.10)概率和为1的条件。
小明醒悟到:原来是这样啊,我明白了。
艾博士:对于类别概率也采用类似的办法,假定每个类别至少存在一个样本,这样类别概率计算公式(5.4)就变成了下式:

讲到这里艾博士问小明:明白这里为什么在分母中加类别数K吧?
小明回答到:明白。跟前面式(5.11)是同样的道理,由于每个类别增加了一个样本数,共有K个类别,相当于增加了K个样本,所以分母中要加上类别数K,以便满足每个类别的概率累加和为1的条件。
艾博士:小明,你按照表5.2给出的数据集,计算一下采用拉普拉斯平滑方法后的概率,就只计算两个类别概率和在不同类别下发长特征几个取值的概率吧?其他也都是大同小异,就不一一计算了。
小明边回答说“好的”边计算起来:
表5.2中共有15个样本,男性和女性两个类别,其中男性有8个样本,女性有7个样本。按照式(5.12)我们计算得到类别概率:
P(男性)=(8+1)/(15+2)=0.5294
P(女性)=(7+1)/(15+2)=0.4706
同样对于发长特征共有短发、中发和长发3个取值,在8个男性类别样本中有6个短发样本、1个中发样本和1个长发样本。按照是(5.11)我们计算得到概率:
P(短发│男性)=(6+1)/(8+3)=0.6364
P(中发│男性)=(1+1)/(8+3)=0.1818
P(长发│男性)=(1+1)/(8+3)=0.1818
同样对于发长特征,在7个女性类别样本中有1个短发样本、3个中发样本和3个长发样本。按照是(5.11)我们计算得到概率:
P(短发│女性)=(1+1)/(7+3)=0.2
P(中发│女性)=(3+1)/(7+3)=0.4
P(长发│女性)=(3+1)/(7+3)=0.4
艾博士检查了小明的计算结果后称赞到:小明计算得真是又快又准确。拉普拉斯平滑方法通过在原有计数基础上加1的方法,解决了因数据不足造成的概率为0问题,这看起来是个小技巧,实际上是有理论依据的,具体我们就不介绍了。
最后我们再举一个采用朴素贝叶斯方法做文本分类任务的例子。
小明:什么是文本分类任务呢?
艾博士:所谓文本分类任务就是对于一个给定文本,按照其内容分配到相应的类别中。比如说我们有4个新闻类别分别为体育、财经、政治和军事,新来了一个新闻稿件,应该属于哪个类别呢?这就是文本分类任务所要完成的。
小明:这倒是一个很有意思的任务。
艾博士:为了完成这个任务,我们首先要收集包含这四个方面内容的新闻稿件作为训练数据集,我们称为语料库。语料库中每篇新闻稿件作为一个训练样本。收集到的每篇新闻稿件要标注好所属的文本类别,以便用于计算朴素贝叶斯分类方法中所用到的各种概率。为了防止出现概率等于0的情况,我们采用拉普拉斯平滑方法。
首先按照式(5.12)计算四个类别的类别概率,以新闻稿件为单位进行计算:
P(文本类别)=(属于该类别的新闻稿件数+1)/(新闻稿件总数+类别数)
比如,体育类的概率:
P(体育)=(属于体育新闻的稿件数+1)/(新闻稿件总数+4)
我们以新闻稿件中用到的单词为特征,每个具体的单词为特征的取值。为此我们事先要建立一个词表,可能用到的单词均包含在此表中。
接下来按照式(5.11)我们计算词表中每个单词在每个类别中出现的概率:
P(单词i│类别k)=(单词i出现在类别k新闻稿件中的次数+1)/(语料库中出现的单词总次数+词表长度)
比如“足球”出现在“体育”类中的概率:
P(足球│体育)=(足球出现在体育类新闻稿件中的次数+1)/(语料库中出现的单词总次数+词表长度)
其中“词表长度”相当于式(5.11)中的“特征可能的取值数 Sk ”,词表中有多少个单词,就相当于有多少个可能的取值。
计算完这些概率,取对数后存储起来以便分类时使用,训练过程就结束了。
当来了一个新的新闻稿件之后,该稿件属于哪个类别呢?按照朴素贝叶斯方法,我们分别将体育、财经、政治和军事4个类别带入式(5.9)中计算,取值最大者就是新稿件所属的类别。

其中N为新稿件的长度,即新闻稿件包含的单词数。这样就用朴素贝叶斯方法实现了对新闻稿件的文本分类。
小明:原来可以这样实现文本分类啊,看起来并不难,回家后我就写个程序看看效果如何。
小明读书笔记
朴素贝叶斯方法是一种基于概率的分类方法,对于待分类样本,计算属于每个类别的概率,将所属概率最大的类别作为分类结果。
根据贝叶斯公式,求待分类样本x所属概率最大的类别可以转化为求下式最大问题:
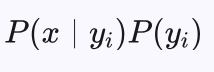
其中 P(yi) 是类别 yi 出现的概率,可以通过训练数据估计得到:

P(x | yi)是类别 yi 中特征取值x的联合概率。由于联合概率存在组合爆炸问题,为此引入特征独立性假设,联合概率:
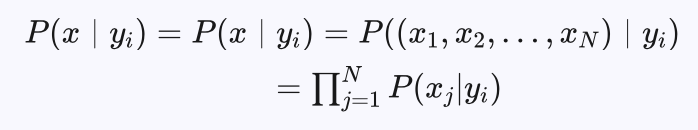
其中 xi 为x第i个特征的取值。
引入独立性假设的贝叶斯分类方法称作朴素贝叶斯方法。概率 P(xj | yi)可以通过训练数据估计得到:

为了防止概率为0的情况出现,一般采用拉普拉斯平滑方法,即默认任何特征均至少有一个取值。
未完待续
未完待续

