第五篇 统计学习方法是如何实现分类与聚类的(四)
清华大学计算机系 马少平
第四节:决策树
——C4.5算法
艾博士:ID3算法是一个被广泛使用的决策树算法,但是也存在一些不足。
小明:ID3算法有哪些不足呢?
艾博士:ID3算法存在的主要问题是,当按照信息增益选择特征时,会倾向于选择一些取值多的特征。
小明有些不解地问到:这是为什么呢?为什么会存在这种倾向性?
艾博士解释说:我们从信息增益的计算方法来分析这个问题。按照式(5.16)信息增益为:
g(D,A)=H(D)-H(D│A)
当数据集确定时,H(D)是固定值,信息增益的大小由特征A的条件熵H(D│A)的大小决定。当特征A的可能取值比较多时,数据集D被划分为多个子数据集,每个子数据集中的样本数就可能比较少,这样对于一个含有比较少样本的子数据集来说,里面只包含单一类别样本的可能性就比较大,这样就会导致条件熵比较小,从而使得信息增益比较大。极限情况下,特征A的取值特别多,以至于每个样本都有一个不同的取值,这样每个子数据集就只含有一个样本,每个子数据集的类别都是确定的。这种情况下特征A的条件熵为0,信息增益取得最大值。但是这样的特征不具有任何归纳能力,泛化能力会非常差。
小明不太明白地说:艾博士,能否举例说明呢?不太明白为什么特征的取值太多,就可能导致泛化能力差。
艾博士:好的,我们举例说明。假设年龄特征就按照真实年龄取值,而刚好每个人的年龄都不一样,假设样本中24岁的是男性,25岁的是女性,26岁、27岁的是男性…,而每个年龄又只有一个样本,这样就完全按照年龄区分了性别,对于待分类样本来说,如果24岁的就是男性、25岁的就是女性,这种情况下的分类结果不是没有任何意义了吗?
小明:明白了,这种情况下确实不具有分类能力了。怎么解决这个问题呢?
艾博士:归根结底出现这个问题的原因还是样本不足造成的。设想一下,如果样本足够多,24岁的样本中有男有女、25岁的样本也有男有女,正常情况下男女的比例应该各占50%左右才正常。在这个比例下,年龄特征的条件熵就会比较大,相应地其信息增益也会比较小。但是在建立决策树过程中,数据集是逐渐被划分为一个个子数据集的,多次划分之后,子数据集中的样本量就会急剧减少,这时用取值比较多的特征对数据集做划分,就更容易出现样本不足的情况,从而造成信息增益大的假象。为解决这个问题,提出了信息增益率的概念。
小明:信息增益率是个什么概念呢?
艾博士:类比一下的话,信息增益好比是绝对误差的话,信息增益率就相当于是相对误差。首先我们给出分离信息(Split Information)的概念,根据分离信息就可以计算出信息增益率。
分离信息本质上还是熵的概念。小明,你说说我们如何计算一个数据集D的熵H(D)?
小明:数据集D的熵H(D)是按照D中的类别标志,计算每个类别的概率 Pi ,然后按照下式计算熵H(D):
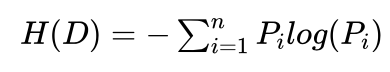
艾博士:对的,就是这样计算,这里的要点是“按照类别的概率计算熵”。可以证明熵的最大值是log(n),这里的n为类别数,log为计算以2为底的对数。所以熵的最大值是与类别数有关的,类别越多,其熵的最大值也越大。当然这里要注意,是熵的最大值越大,不是说类别多了熵就一定大,与数据集D中样本分布有关。
与通常用分类概率计算熵不同,分离信息是按照特征的取值计算概率,然后按照该概率值计算熵,与样本的分类无关。所以说分离信息本质上还是熵,只是计算角度不同。我们用SI(D,A)表示特征A在数据集D上的分离信息,则:

其中n为特征A的可能取值数。
小明:从公式看分离信息的计算确实就是在计算熵,只是概率的计算方法是按照特征取值计算,而不是按照类别计算。
艾博士:刚刚说过,类别越多,熵的最大值就越大。对于分离信息来说,就是特征取值越多,分离信息的最大值越大。所以可以用分离信息作为惩罚项,对信息增益进行惩罚,这样就得到了特征A对数据集D的信息增益率Gr(D,A) :
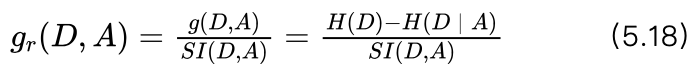
信息增益率就是信息增益除以分离信息,对于取值比较多的特征,其分离信息可能比较大,这就弱化了按照信息增益选择特征时倾向于选择取值多的特征的问题。
小明:明白了,原来是这样的。
艾博士:下面我们给一个计算信息增益率的例子。
在前面男女性别分类数据集中,共有15个样本,发长特征有短发、中发和长发三个取值,其中取值为短发的有7个样本,取值为中发的有4个样本,取值为长发的有4个样本,那么发长特征在该数据集上的信息增益率是多少呢?小明你计算一下。
小明:我们前面已经计算过在这个数据集上,发长特征的信息增益为0.2880,我们直接采用这个结果,不再重复计算。
按照式(5.17),发长特征的分离信息为:

看到小明计算完毕,艾博士接着讲解到:将ID3算法中按照信息增益选择特征,修改为按照信息增益率选择特征,就成为了C4.5算法,也就是说,C4.5算法是对ID3算法的一种改进算法。我们就不给C4.5算法的具体描述了,除了按照信息增益率选择特征以外,二者基本一致。
小明:“二者基本一致”,那么就是说还有不一致的地方?
听到小明的问题,艾博士哈哈大笑起来:确实还有一些小的变化和其他的改进地方。下面我们看看在C4.5算法中有哪些其他改进的地方。
信息增益率是信息增益除以分离信息,如果数据集按照特征取值划分为几个子数据集后,不同子数据集中样本的数量偏差比较大,则分离信息就比较小,从而导致比较大的信息增益率。比如某个特征只有a、b两个取值,其中绝大部分样本取a值,只有少量样本取b值,则取值为a的概率接近于1,取值为b的概率接近于0,该特征的分离信息就比较小,从而导致比较大的信息增益率。但是造成这种极端不平衡数据划分的特征对决策树来说并不是一个好的特征,因为其信息增益可能也比较小,应尽量避免使用。为此在C4.5算法中的解决方法是,先选择几个信息增益大的特征,然后再从这几个特征中选择信息增益率最大的特征,这样可以保证被选中的特征不仅具有比较大的信息增益率,也同时具有比较大的信息增益,在信息增益和信息增益率之间有所平衡。
小明:那么这里的“几个信息增益大的特征”选择几个才合适呢?
艾博士:一般可以选信息增益大于平均值的特征,有几个特征的信息增益大于平均值就选几个。
C4.5算法的另一个改进是特征可以取连续值。
小明:特征取连续值是什么含义呢?
艾博士:简单说,就是允许某些特征按照实际值取值,而不需要离散化处理。比如,发长特征就可以允许取连续值,样本中直接记录其实际发长就可以了。比如3厘米、10厘米等,而不再需要离散化成短发、长发等。
小明有所不解地问到:艾博士,前面您不是讲过,这样的特征具有非常多的取值,泛化能力很差吗?C4.5算法主要的改进也是采用信息增益率选择特征,目的就是尽量不采用这样的特征。为什么在C4.5算法中反而又允许这样的取值呢?
艾博士:小明能提出这样的问题说明你确实在认真思考问题,如果将头发的每一个长度都是作为离散值使用的话,确实会出现你说的问题,之所以对ID3算法做改进提出C4.5算法,也确实是为了尽可能避免这样的问题出现。但是在C4.5算法中这样的特征是当作连续值处理的,如果一个特征被标注为连续取值后,其处理方法与离散值特征并不一样。
小明:如何处理连续特征呢?
艾博士:在C4.5算法中对于连续特征是这样处理的。假设特征A是连续特征,按照特征A的取值对数据集D中的样本从小到大排序,排序后第i个样本特征A的取值为ai 。对于D中任意两个相邻的样本i和i+1,我们计算这两个样本特征A的中间值 bi ,即:

然后按照bi 值将数据集D划分为两个子数据集,特征A取值大于bi 的样本为一个子数据集,小于等于bi 的样本为另一个子数据集。经过这样划分后我们就可以计算该特征的信息增益率。对于具有m个样本的数据集D,排序后任意相邻两个样本可以计算得到一个 bi ,每个 bi 都可以将数据集D划分为两部分,计算出不同的信息增益率。其中最大的信息增益率作为特征A的信息增益率,与其他特征的信息增益率进行比较,选出信息增益率最大的特征参与决策树的建立。如果特征A的信息增益率刚好最大,则采用信息增益率最大时所对应的 bi 将数据集D划分为两个子数据集。这样就实现了对连续取值特征的处理。
小明:我有些明白了。实际上,对于连续取值的特征,C4.5算法自动将该特征离散化为两个取值,大于bi 是一个取值,小于等于bi 是一个取值,而在多个 bi中选择信息增益率最大的作为最佳划分。
艾博士;小明总结得很好,从本质上来说,C4.5算法处理的还是特征的离散值,只是对于连续特征自动按照信息增益率选择一个比较好的离散点,将该特征离散化为二值后再做处理。
小明:这样的话,对于连续特征就只能将数据集D划分为两个子数据集了?而不像其他离散特征那样,有多少个取值就将数据集D划分为几个子数据集。
艾博士:就是这样的。还有一点需要强调一下。对于离散特征A来说,如果该特征将数据集D划分为子数据集 D1 和D2 ,则在进一步处理 D1 和D2 时,特征A要从特征集中删除。但是如果特征A是连续取值的话,则特征A还需要保留在特征集中,还可以继续在子数据集 D1、D2 中使用。这一点也是连续特征与离散特征的不同之处。
小明:这一点如果您不提醒的话还真容易忽略。想一想也容易理解,因为对于连续特征来说,每次只是利用 bi 值将数据集划分为了两个子数据集,在子数据集中还可以再利用其他的 bi 做进一步的划分,所以该特征必须被保留在特征集中。
艾博士:下面我们再举一个例子说明连续特征时信息增益率是如何计算的。
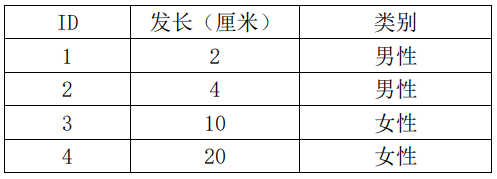
假设发长是连续取值特征,样本如表5.4所示,这里我们忽略其他特征的取值。
表5.4 男女性别分类样本
首先计算数据集D的熵,D中共有4个样本,其中男性2个、女性2个,所以熵H(D)为:
H(D)=-(P(男性) log(P(男性))+P(女性) log(P(女性)) )
=-(2/4 log(2/4)+2/4 log(2/4) )
=1
发长有4个取值,样本按发长取值排序,分别可以在2与4、4与10和10与20之间分割,得到数据集的三种划分结果。
(1)第一个分割点:

子数据集 D1 的熵:
H(D1)=-(P(男性) log(P(男性))+P(女性) log(P(女性)) )
=-(1/1 log(1/1)+0/1 log(0/1) )
=0
子数据集D2的熵:
=-(P(男性) log(P(男性))+P(女性) log(P(女性)) )
=-(1/3 log(1/3)+2/3 log(2/3) )
=0.9183
根据式(5.15)有分割点 b1=3 时发长特征的条件熵:
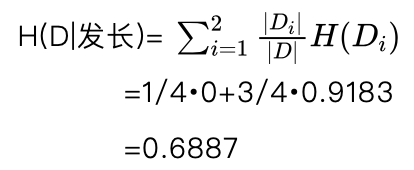
根据式(5.16)有分割点 b1=3 时发长特征的信息增益为:
g(D,发长)=H(D)-H(D│发长)
=1-0.6887
=0.3113
根据式(5.17)有分割点 b1=3 时发长特征的分离信息为:

这样,根据式(5.18)有分割点 b1=3 时发长特征的信息增益率为:
gr(D, 发长) =g(D,发长)/SI(D,发长)
=0.3113/0.8113
=0.3837
(2)第二个分割点:
b2 =(4+10)/2=7
发长值比b2小的样本用样本ID的集合表示为:
D1={1,2}
发长值比b2大的样本用样本ID的集合表示为:
D2 ={3,4}
子数据集 D1 的熵:
H(D1)=-(P(男性) log(P(男性))+P(女性) log(P(女性)) )
=-(2/2 log(2/2)+0/2 log(0/2) )
=0
子数据集 D2 的熵:
H(D2)=-(P(男性) log(P(男性))+P(女性) log(P(女性)) )
=-(0/2 log(0/2)+2/2 log(2/2) )
=0
根据式(5.15)有分割点b_2=7时发长特征的条件熵:
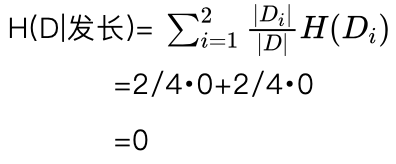
根据式(5.16)有分割点b2=7 时发长特征的信息增益为:
g(D,发长)=H(D)-H(D│发长)
=1-0
=1
根据式(5.17)有分割点 b2=7 时发长特征的分离信息为:

这样,根据式(5.18)有分割点 b2=7 时发长特征的信息增益率为:

(3)第三个分割点:
b3 =(10+20)/2=15
发长值比 b3 小的样本用样本ID的集合表示为:
D1 ={1,2,3}
发长值比 b3 大的样本用样本ID的集合表示为:
D4 ={4}
子数据集 D1 的熵:
H(D1) =-(P(男性) log(P(男性))+P(女性) log(P(女性)) )
=-(2/3 log(2/3)+1/3 log(1/3) )
=0.9183
子数据集 D2 的熵:
H(D2) =-(P(男性) log(P(男性))+P(女性) log(P(女性)) )
=-(0/1 log(0/1)+1/1 log(1/1) )
=0
根据式(5.15)有分割点 b3 =15时发长特征的条件熵:
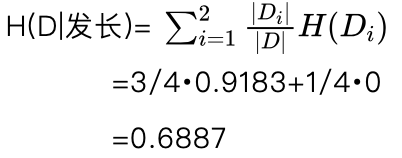
根据式(5.16)有分割点 时发长特征的信息增益为:
g(D,发长)=H(D)-H(D│发长)
=1-0.6887
=0.3113
根据式(5.17)有分割点 时发长特征的分离信息为:

这样,根据式(5.18)有分割点 b3 =15时发长特征的信息增益率为:

这样我们就得到了三个分割点的信息增益率分别为:0.3837、1、0.3837,其中分割点为7时的信息增益率最大,这样我们就以该信息增益率作为发长特征对数据集D的信息增益率。
未完待续

