第四篇 如何用随机算法求解组合优化问题（八）
清华大学计算机系 马少平
第八节：遗传算法
艾博士：遗传算法是另一种求解组合优化问题的随机算法，是受达尔文进化论的启发而提出来的一种优化算法。
小明：这个算法竟然和进化论有关。
艾博士：小明，你大概了解进化论吧？
小明：在生物课上老师讲过达尔文的进化论，核心思想就是八个字：“物竞天择、适者生存”。记得老师用长颈鹿举例说：早期的长颈鹿脖子虽然有长有短，但是差别并不大，正常环境下，地上有草，有灌木丛，也有树，这些都可以作为长颈鹿的食物，无论脖子长短都不影响长颈鹿的生存。但是由于环境恶化，作为长颈鹿食物的草和灌木丛逐渐减少，适于长颈鹿生存的食物越来越少，慢慢地几乎只剩下树叶是其赖以生存的食物。这样脖子长的长颈鹿由于更容易获取食物就比较容易生存下来，而脖子短的长颈鹿由于获取食物困难，就比较容易被淘汰。经过多少代的遗传、自然选择之后，脖子长的长颈鹿比较适应生存环境，更容易生存下来，而脖子短的长颈鹿难以适应生存环境，逐渐被淘汰，慢慢地长颈鹿就成为了现在大家所看到的各个都是长脖子了。
艾博士：小明很好地解释了进化论“物竞天择、适者生存”的核心思想。
根据达尔文的进化论，在生物进化的过程中，只有那些最能适应环境的种群才得以生存下来。生物的进化过程可以用如图4.15所示的进化圈表示，这是一个长期的循环演化过程。
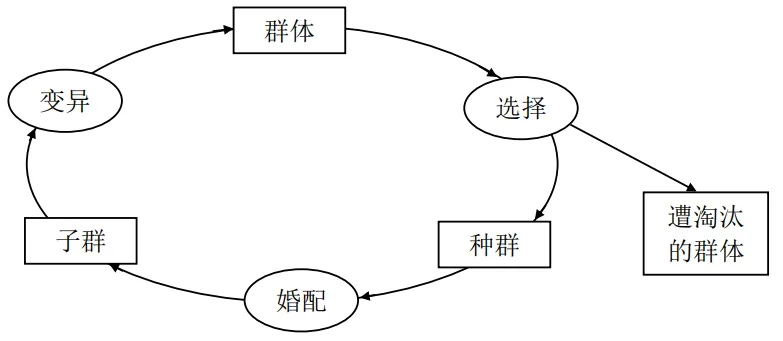
图4.15. 生物进化圈示意图
该进化圈以群体为一个循环的起点。按照优胜劣汰的原则，经过自然选择后，一部分群体由于无法适应环境而遭淘汰退出进化圈。在自然界中，自然选择包括恶劣的天气和气候、食物的短缺、天敌的侵害等。另一部分群体，由于适应环境的能力强而生存下来。它们或者是因为身体强壮而逃脱天敌的侵害，或者因为耐寒冷、耐饥饿能力强而存活下来。总之，这些群体之所以能够生存，是因为它们具有某种适应周围环境的能力。从适应环境的能力方面来说，这些群体从总体上考察是优良的，被淘汰的是那些体弱病残、不能适应环境生存的个体。即便因偶然因素一些弱者侥幸生存了下来，但在婚配的竞争中它们也往往处于劣势。因此可以说只有那些适应环境能力强的优良品种才能够成为新的种群。经过种群的婚配，繁衍出下一代子群。一般来说子群中的个体遗传了父母双亲的优势，加快了后代的进化，使之更能够适应环境。比如，一个身体强壮的个体和一个耐寒冷能力强的个体繁衍的后代可能会同时具有身体强壮和耐寒冷的能力。在进化的过程中，个别的个体可能会发生一些变异，从而产生新的个体，使得群体的组成更加多样化。综合以上过程，经过一个循环的进化，新的群体生长起来，取代旧群体，又进入新的一轮进化之中。经过长期的竞争、淘汰、进化过程，最终的群体中生存下来的是那些最能适用环境生存的优秀个体。
总之，生物在进化过程中，经过优胜劣汰的自然选择，会使得种群逐步优化，经过长期的演化，优良的物种得以保留。不同的环境，不同物种的基因结构，导致最终的物种群不同，但它们都有一个共同的特征：最能适应自己所处的生存环境。
艾博士总结说：从最优化的角度来讲，环境可以认为是约束条件，而进化选择之后的获胜者可以认为是在给定约束条件下的最优解。不同的约束条件，最优解也是不同的，所谓的最优解都是相对于约束条件而说的。就好比说在那个特殊的环境下进化出了长颈鹿，如果当初没有这样的环境，还是这个群体可能就进化出了其他的物种。如果不是在这个特殊的环境下，也许这个世界上就没有了长颈鹿，而被其他某种物种所代替。
小明：想一想这个世界之所以有千奇百怪的动物，也许就是不同的环境造成的吧？那么如何借助进化论的思想发展出遗传算法呢？
艾博士：受达尔文进化论“物竞天择、适者生存”思想的启发，美国密执根大学的Holland教授把最优化问题与生物进化过程对应起来，将生物进化的思想引入到复杂问题求解中，提出了求解优化问题的遗传算法。同模拟退火算法将组合优化问题与退火现象建立类比关系一样，这里关键的问题是如何将组合优化问题与进化过程建立对应关系。
染色体是物种的基本表达，进化也发生在染色体上，不同的染色体也体现了相应物种适应环境的能力。在遗传算法中，最优化问题的一个解对应生物中的个体，首先对优化问题可能的解，也就是个体进行编码，编码后的解与染色体相对应，也称作染色体。个体、解、染色体指的是同一个事情，通常并不对它们加以严格的的区分，不同的场合下也会混用，如果说区别的话，个体指的是解，染色体指的是解的编码。组成染色体的元素称为基因。一个群体由若干个个体组成，个体的数量称为群体的规模。与自然界中的生存环境相对应的，是遗传算法中的适应函数。该函数是解的函数，是对一个解适应环境程度的评价。适应函数的构造一般与优化问题的指标函数相关，简单的情况下，直接用指标函数或者指标函数经过简单变换后作为适应函数使用。一般情况下，适应函数值越大表示所对应的个体适应环境的能力越强。适应函数起着自然界中环境的作用，当适应函数确定后，自然选择规律将以适应函数值的大小来决定一个个体是否继续生存下去的概率。生存下来的个体成为种群的一员，以一定的概率进行婚配，繁衍出下一代群体。婚配是一个繁衍过程，发生在两个染色体之间，作为双亲的两个染色体，交换部分基因之后，生殖出两个新的染色体，即问题的新解，作为新个体加入到群体中。婚配在遗传算法中称作交叉操作，是遗传算法区别于其他优化算法的主要特征之一。在进化的过程中，染色体的某些基因可能会发生变异，即表示染色体的编码发生了某些突变。一个群体的进化需要染色体的多样性，而变异对保持群体的多样性具有一定的作用。
表4.7给出了遗传算法与生物进化之间的对应关系。
表4.7：生物进化与遗传算法之间的对应关系
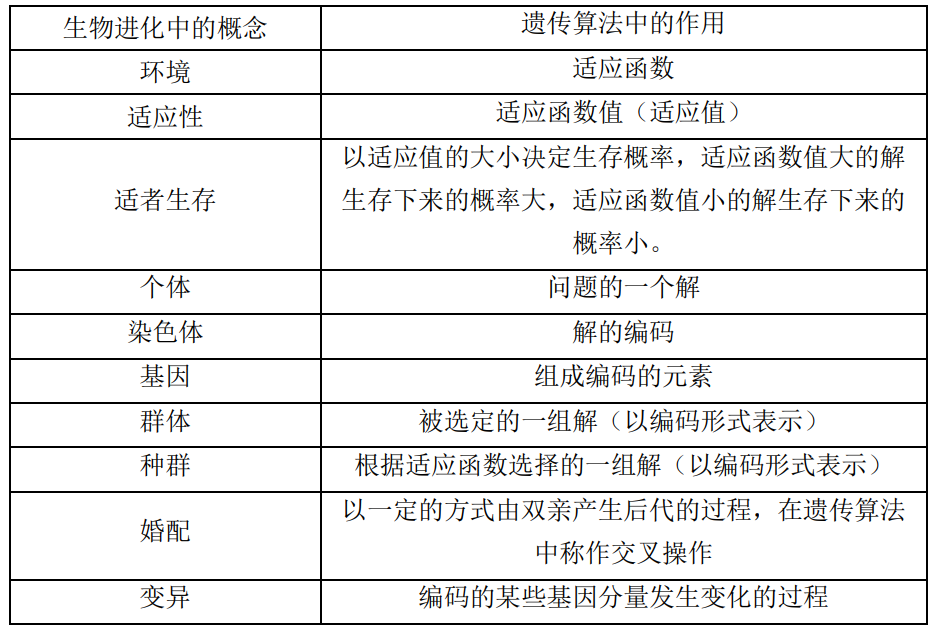
小明看着表4.7所示的生物进化与遗传算法之间的对应关系，挠挠头说：听完您的介绍，虽然大体明白了什么意思，但是还是感觉有些虚，不知道算法究竟是如何操作的。
艾博士：这些还只是一些基本思想，想不清楚也是正常的。下面我们具体讲解一下，再结合一些具体实例，就容易明白了。
为了更容易理解遗传算法与生物进化的对应关系，我们结合下面这个例子进行一步步讲解。
例：求解下列函数的最大值，其中x取值为区间[0, 31]上的整数。
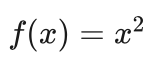
该问题比较简单，因为在区间[0, 31]上f(x)是单调上升的，其最大值显然在x=31处取得。我们关注的是如何利用遗传算法求解这个最大值问题。
艾博士讲解说：在该问题中，x的取值范围为区间[0,31]上的整数，因此0到31的每个整数都可能是问题的解，x每个可能的取值都可以看做是一个个体。首先我们要对个体进行编码，编码的要求是，任何一个x可能的取值，也就是可能的解，与编码之间具有一一对应的关系。就是说对于任意一个解都有唯一的编码，而任何一个编码都唯一对应一个解。由于0到31的整数共有32个，如果采用二进制编码的话，可以考虑用5位二进制数进行编码。比如，整数0可以表示为00000，整数1可以表示为00001，整数2可以表示为00010，......，整数31可以表示为11111。
小明：二进制编码就是将整数表示为对应的二进制数吗？
艾博士：不是这样的。只要解和编码之间具有一一对应关系就可以了，并不要求整数和二进制编码之间具有相等的关系。比如在这个例子中，我们也可以反过来用11111表示整数0，用00000表示整数31。
这样得到的每一个编码就是一个染色体，其中的0、1就是基因，而多个染色体，也就是多个个体构成了一个群体。
小明：原来是这样的的对应关系啊，通过这个例子就容易懂的多了。
艾博士：生物是通过婚配繁衍后代的，其特点是子女的染色体具有父母双方基因的特征。在遗传算法中通过交叉操作达到类似生物繁衍后代的过程，由双亲产生后代。
小明：遗传算法中的繁衍后代过程为什么叫交叉操作呢？
艾博士：一会我们介绍到交叉操作是如何进行的你就明白了。交叉操作发生在两个染色体之间，由两个被称之为双亲的父代染色体，经交叉操作后产生两个具有双亲的部分基因的新的染色体，这两个新的染色体被称作后代。下面我们还是以二进制编码形式为例，介绍交叉操作的具体操作过程。
设a、b是两个进行交叉操作的双亲染色体：
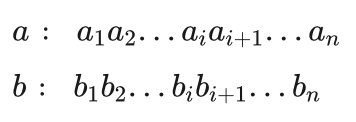
其中ai 、bi 取值0或者1，是组成染色体的基因。交叉操作是这样进行的：随机地产生一个交叉位设为i，则a、b两个染色体从i+1以后的基因进行交换，得到两个新的染色体即两个后代。图4.16给出了两个染色体的交叉示意图。
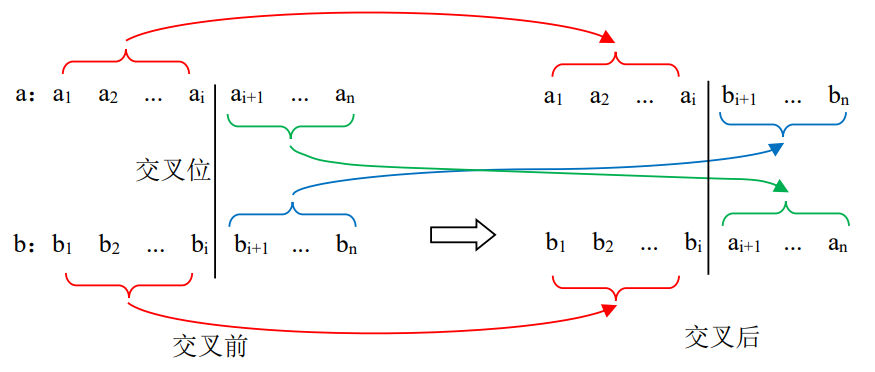
图4.16 染色体交叉示意图
从图中可以看出，后代1的染色体由两部分组成，交叉位之前部分来自双亲1，而交叉位之后部分来自双亲2。而后代2刚好与后代1相反，交叉位之前部分来自双亲2，而交叉位之后部分来自双亲1。
例如，对于 x1=11001 和 x2=01111 两个染色体，当交叉位等于2时，产生两个后代染色体 y1 和 y2 ：
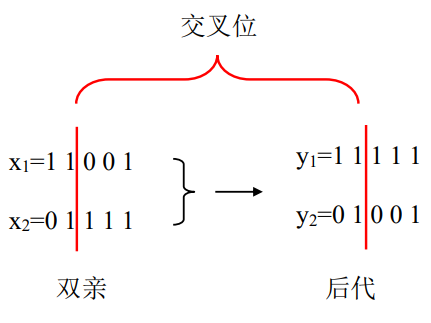
讲到这里艾博士问小明：小明，你明白了为什么遗传算法中的繁衍后代过程叫交叉操作了吧？
小明马上回答说：明白了，“交叉”一词很形象地反应了遗传算法中繁衍后代的具体操作方法。
艾博士：在进化过程中，交叉操作通常是以一定的概率 Pc 发生。从新种群中随机选择两个染色体作为双亲，然后以概率 Pc 进行交叉操作。如果发生交叉操作，则将其两个后代代替两个双亲放入到种群中。如果没有发生交叉操作，则两个双亲原样放入到种群中。
讲到这里，艾博士问小明：这里的“以概率 Pc 进行交叉操作”你知道如何实现吧？
小明回答说：类似问题我们已经多次遇到，用随机数函数random(0, 1)产生一个0、1之间均匀分布的随机数，当该随机数小于概率 Pc 时，则发生交叉操作，否则就不发生交叉操作。就实现了“以概率 Pc 进行交叉操作”。
艾博士接着讲到：生物进化过程中，变异起到了重要的作用。在遗传算法中，所谓变异就是某个基因发生了突变。在二进制编码中，基因只有0和1两种情况，所以当发生变异时，该基因或者是由1变成0，或者是由0变成1。例如对于染色体x=11001，如果变异位发生在第三位，由于第三位是0，所以变异后第三位由0变成了1，则变异后的染色体变成了y=11101。
小明：艾博士，这里的第几位是怎么数的呢？
艾博士：是从左到右数的，最左边为第一位，其他以此类推。
小明：明白了。
艾博士：变异对于一个群体保持多样性具有好处，但也有很强的破坏作用，因此总是以一个很小的概率 Pm 来控制变异的发生。一旦一个染色体按概率 Pm 发生了变异，则要随机产生一个变异位，在该位置的基因发生变异操作。
艾博士：接下来我们看适应函数应该如何定义。由于该问题要求解f(x)的最大值，很自然的就可以想到直接用f(x)作为适应函数。因为适应函数值越大的个体被选择保留下来的概率越大，我们又刚好要求f(x)的最大值，所以可以直接用f(x)作为适应函数。适应函数并不是总是和希望求解的指标函数是一样的，为了区别起见我们用F(x)表示适应函数。在该问题中，F(x)=f(x)。
小明：什么情况下适应函数和希望求解的最优值不一样呢？
艾博士：一般来说，遗传算法适用于求解最大值问题，如果是求解最小值问题，就需要对指标函数做一个变换，变成求解最大值问题。另外，适应函数要求大于等于0，如果待求解函数最大值也是小于0的，就需要对该函数加一个比较大的常数，使得函数值大于0。还有的情况下，为了加快求解的速度也会对指标函数做一定的变换后再作为适应函数使用。这些内容我们后续会一一介绍。
适应函数值——简称适应值，表示个体对环境的适应程度，适应值越大说明适应能力越强。依据适应值的大小对群体中的个体进行选择，就体现了进化论中“物竞天择，适者生存”的核心思想。从规模为N的群体中，依据个体适应值的大小随机选择若干个个体构成新的种群，这一过程称作选择操作。选择操作前后群体规模可以相同，也可以不同，为了叙述方便，我们假定二者的群体规模大小是一致的，即从一个群体规模为N的群体中，依据适应值随机地选择N个个体构成新的种群。由于是依据适应值的大小随机选择的，因此虽然选择操作前后群体的规模大小一样，但是两个群体并不完全一样，因为适应值大的个体可能会多次从群体中选出，而适应值小的个体可能会因没有机会选中而被淘汰。因此一些适应值大的染色体可能会重复出现在种群中，而一些适应值小的染色体则可能被淘汰。这一点体现的正是自然界中“物竞天择、适者生存”的进化规律。
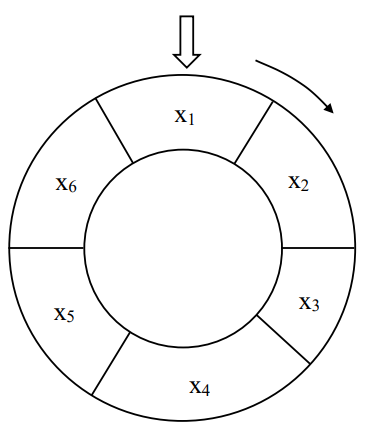
图4.17 “轮盘赌”示意图
小明：这样看来适应函数就相当于生存环境，如何做到依据适应值从群体中选择个体呢？
艾博士：可以有多种方式从群体中选择存活的个体，只要能满足“适应值大的个体被选中的概率大，适应值小的个体被选中的概率小”这个原则就可以。其中被经常使用的是一种被称之为“轮盘赌”的方法。
小明：“轮盘赌”？是一种什么方法呢？
艾博士：以前每逢节假日公园里都有很多游戏，其中就有与图4.17所示类似的“幸运大转盘”游戏。
小明看到图马上说：我小时候玩过类似的游戏。一个大的转盘上画有多个小扇区，有大有小，每个扇区上写有各种不同的奖品。用力转动转盘，当转盘停下来时，指针指向了哪个扇区，就可以获得该扇区写的奖品。
艾博士：对，就是这种玩法。转盘上划分的扇区大小，决定了一个扇区被选中的概率，越大的扇区被选中的概率越大，越小的扇区被选中的概率越小。
所以你喜欢的东西总是写在一个很小的扇区上，而最大的扇区……
还没等艾博士说完，小明抢先说到：最大的扇区总是“谢谢”，我就多次转到“谢谢”。
听小明说完，艾博士哈哈大笑起来：就是这样的。如果群体中每个个体对应一个转盘的扇区，而扇区的大小与个体的适应值相对应，就可以采用这种“轮盘赌”的方法对个体进行选择了。
小明：这种方法倒是简单易行，也能体现出“适应值大的个体被选中的概率大，适应值小的个体被选中的概率小”的这个原则，但是如何实现呢？总不能让计算机去转转盘吧？
艾博士听完又是哈哈大笑：当然不能让计算机去转转盘，我们可以通过模拟的方法实现“轮盘赌”。
小明：怎么模拟呢？
艾博士：首先我们简化“轮盘赌”，假定每次最多转一圈。或者说，前面转的若干完整的圈对于最终选中了哪个扇区没有关系，我们只关心最后一圈（实际上是0到1圈之间）就可以了。我们将转盘的扇区展开成一个长度为1的长条，长条被划分为N块，每块对应群体中的一个个体，每块的大小为对应个体被选中的概率。其中个体xi被选中的概率由下式给出：
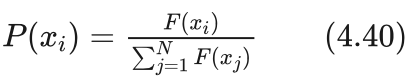
其中N为群体的规模， xi（i=1,2,...,N） 为群体中的个体， F(xi) 为个体 xi 的适应值。
如图4.18所示是一个含有8个个体的“轮盘赌”示意图，设想有一个指针r沿着长条从左到右移动，当指针停止时，指针所指向块所对应的个体就是被选中的个体。
小明：现在的问题就是如何模拟指针r移动。
艾博士：这个问题很容易解决，用随机数函数random(0, 1)产生一个0、1之间均匀分布的随机数就可以实现，该随机数的大小就决定了指针r的位置。
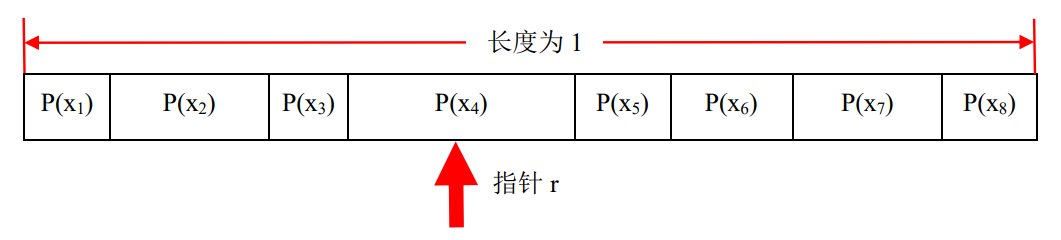
图4.18 模拟“轮盘赌”示意图
下面给出的就是模拟“轮盘赌”的具体算法。该算法依次累加个体xi的被选择概率，当累加值第一次大于随机数r时，则最后一个被累加的个体即为被选中的个体，相当于指针指向了该个体。
“轮盘赌”算法
（1）r=random(0, 1)，s=0，i=0；
（2）如果s＞r，则转（4）；
（3）i=i+1，s=s+p( xi )，转（2）
（4） xi 即为被选中的染色体，输出i；
（5）结束。
其中random(0, 1)是一个产生在[0, 1]之间均匀分布的随机数函数，一般的编程语言中都会提供一个类似的随机数函数。
这样经过N次“轮盘赌”之后，就可以从一个规模为N的群体中选择出一个新的规模同样为N的种群。这就是遗传算法的选择过程。
小明：艾博士，您给举一个例子吧，选择过程如何按照概率从群体中选择N个个体得到新的种群？
艾博士：好的。还是以前面提到的求 f(x)=x^2 在区间[0,31]上最大值的问题为例。我们以5位二进制对该问题进行编码。假设当前的群体为：
01101，11000，01000，10011
对应x的4个取值分别为13、24、8、19，适应函数按照F(x)=x^2计算，分别为169、576、64、361，选择概率按照式（4.40）计算，得到4个个体的选择概率：
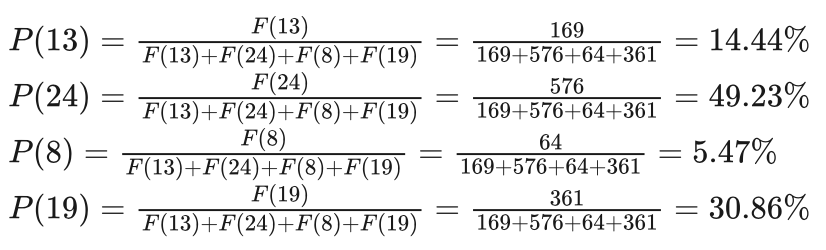
如上图所示，按照轮盘赌算法我们从该群体中选择4次，假设第一次random(0, 1)函数产生的随机数为0.8，则x=19这个个体被选中。第二次产生的随机数为0.3，则x=24这个个体被选中。第三次产生的随机数为0.1，则x=13这个个体被选中。第四次产生的随机数为0.5，则x=24这个个体再次被选中。至此，x=13、x=19两个个体分别被选中1次，x=24被选中了2次，而x=8被淘汰。这样就得到了新的种群：
01101，11000，11000，10011
小明：最后得到的种群与random(0, 1)产生的随机数关系很大啊，不同的随机数可能会有不同的结果。
艾博士：确实是这样的，这也是随机算法的特点，每次的结果具有一定的随机性。但是选择概率大的个体被选中的概率大，这一点是不变的。
艾博士接着说：“轮盘赌”方法是遗传算法中选择过程常用的方法，但是由于存在随机性，对于调试程序会造成一些不便。下面再介绍一种“确定性”选择方法，该方法完全按照概率值的大小进行选择操作，而不依赖于随机数，所以称作“确定性”方法。该方法对于调试程序比较方便。
对于规模为N的群体，一个选择概率为P(xi)的个体xi被选中次数的期望值e(xi)为：
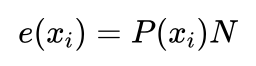
小明不解地问到：期望值是个什么概念呢？
艾博士：期望值可以近似看做就是平均值。假设按照“轮盘赌”方法进行了很多次选择操作，每次产生一个种群。由于具有一定的随机性，则每次得到的种群中某个个体被选中的次数可能不一样。但是进行足够多次选择操作之后，某个体被选中的平均值会逐渐趋于一个稳定值，该值就是该个体被选择次数的期望值。比如前面的例子中，x=24被选中了2次。如果多做几次实验，有时可能被选中3次，有时可能被选中1，甚至也可能会被淘汰，虽然被淘汰的概率很小。如果经过足够多次实验之后，当假定群体规模为4时，x=24被选中的平均值会逐渐趋近于e(24)=P(24)×4=49.23%×4=1.97次。这就是期望值的含义。
小明：原来是这样啊，我明白了。所以“确定性”方法不像“轮盘赌”方法那样每次随机做选择了，而是按照选中的期望值直接进行选择？期望值是多少就选择多少次吗？
艾博士：小明很聪明，稍微点拨一下马上就明白了。但是期望值一般是带有小数的，而选择次数必须是整数，所以需要特殊处理一下，但是基本思想确实就是这样的。
小明：对啊，还有这样的问题呢，选择次数必须是整数才行。
艾博士接着讲解说：为了叙述方便，我们将个体xi被选中次数的期望值划分为整数部分和小数部分，其中整数部分用ei(xi) 表示，小数部分用 ef(xi)表示。比如x=24被选中次数的期望值为1.97次，则 ei(24)=1 ，ef(24)=0.97 。
这样，“确定性”方法对于群体中的每一个体 xi，首先按照期望值的整数选择 ei(xi) 次。这样共选择到的个体总数为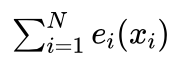
。因为我们要求新的种群规模也是N，目前只是按照期望值的整数部分进行了选择，一般情况下选中的个体数量不足N个，需要补充 
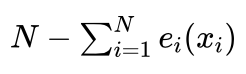个才能使得种群规模达到N个。补充的方法是，按照期望值的小数部分 ef(xi) 从大到小对个体排序，依次取出前 
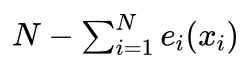个个体。这样就一共得到了N个个体，以这N个个体组成新的种群。
讲到这里艾博士总结说：以上我们通过实例具体讲解了遗传算法与生物进化之间的对应关系，以及选择、交叉和变异三种主要的操作。讲到这里，我想小明对遗传算法应该有了大体上的了解了吧？
小明：是的。通过您结合具体实例的详细讲解，我对遗传算法有了基本的了解，大体上明白了算法的执行过程。
艾博士：好的。下面我们就给出遗传算法的具体描述。其中，每完成一轮选择、交叉和变异操作就认为是进化了一代，每一代中群体的规模是固定不变的，变量t表示当前的代数。当算法结束时，进化过程中适应值最大的解即为求得的最优解。
遗传算法：
（1）给定群体规模N，交配概率 Pc 和变异概率 Pm ，t＝0；
（2）随机生成N个个体作为初始群体；
（3）对于群体中的每一个个体 xi(i=1,2,...,N) 分别计算其适应值 F(xi) ；
（4）如果算法满足停止准则，则转（10）；
（5）对群体中的每一个体xi依下式计算其选择概率：
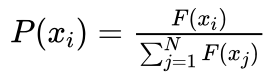
（6）依据选择概率，从群体中随机地选取N个个体，得到种群；
（7）依据交叉概率 Pc 从种群中随机选择两个个体作为双亲进行交叉操作，其两个后代进入新的群体，种群中未进行交叉操作的个体，直接复制到新群体中；
（8）依据变异概率Pm 从新群体中选择个体进行变异操作，用变异后的个体代替新群体中的原个体；
（9）用新群体代替旧群体，t=t+1，转（3）；
（10）进化过程中适应值最大的个体，作为算法得到的最优解输出；
（11）结束。
艾博士：以上给出的是遗传算法的一个基本框架，有些算法细节并没有给出，比如算法第（4）行“如果算法满足停止准则”，并没有说明什么情况下算法就可以结束了。这些我们后面还会结合具体情况给予讲解。另外我要特别强调一下，算法第（10）行“进化过程中适应值最大的个体”这句话的具体含义是指，从第0代开始就要设置一个变量用于保留进化过程中到目前为止得到的最好解，算法最终以该解作为最后的输出，而不是算法结束时最后一代中最好的解。也就是说，算法输出的结果不一定出现在最后一代中，可能是之前某一代中的一个结果。极限情况下，是第0代的结果也是有可能的。这一点是初学者最容易犯的错误，往往会将最后一代中得到的最好解输出。这是不对的，一定要记住这一点。
小明：如果您不提醒我还没有注意到遗传算法的这个特点。我印象中在模拟退火算法中，输出的结果是算法结束时所得到的解，并没有要求记录退火过程中得到的最好解。
艾博士回答说：对于模拟退火算法来说最后得到什么解输出的就是什么解，而遗传算法有所不同，必须记录遗传过程中得到过的最好解，并以此作为算法的最后输出。
小明：明白了。模拟退火算法是不是也可以这么助理呢？一直保留一个退火过程中的最好结果作为最后的输出。
艾博士：对于模拟退火算法也是可以这么做的，但是从理论上来说，模拟退火算法并不要求这么做，虽然这么做在实际中确实可以提高获得最优解的可能性。
小明：了解了。虽然理论上来说模拟退火算法最后以概率1获得最优解，但是实际使用时还是有可能陷入局部最优解。这种情况下，由于在退火过程中状态一直在做各种交换，有可能在某次交换中获得一个比最终结果更好的解，输出这个结果对我们求解更好的结果也是有利的。
小明读书笔记
受达尔文进化论“物竞天择，适者生存”思想的启发提出了遗传算法。生物之所以产生进化，是优胜劣汰选择的结果，“适”者即为“优”者，什么是“优”，完全依靠自然选择。
遗传算法在生物进化和组合优化问题之间建立对应关系，用适应函数对应环境，适应值对应适应性，以适应值的大小决定生存概率，按照生存概率进行优胜劣汰选择，对应进化过程中的“适者生存”。问题的一个解对应生物个体，解的编码对应个体染色体，组成编码的元素对应基因。遗传算法通过选择操作、交叉操作和变异操作，按照进化思想求解最优解。
常用的选择操作是“轮盘赌”方法，通过模拟轮盘赌的方式按照概率选择种群，适应值越大的个体被选择的概率越大。确定性方法也是一种选择方法，其基本思想是按照选择次数的期望值选择种群。
交叉操作由两个双亲产生两个后代，体现了生物繁衍后代的过程。
变异操作是生物多样性的体现，一般以小概率发生，在遗传过程中起着重要的作用。交叉操作和变异操作是遗传算法必须有的两个操作。
遗传算法在求解过程中一定要保留遗传过程得到的最好结果，并以此为输出。最好结果不一定出现在最后一代中，可能是在其中的某一代中出现。这一点必须要牢记在心。
未完待续