第四篇 如何用随机算法求解组合优化问题(九)
清华大学计算机系 马少平
第九节:遗传算法应用举例
艾博士:下面我们通过前面提到过的求最大值的例子,说明遗传算法是如何求解这个问题的。
例:求解下列函数的最大值,其中x的取值为[0, 31]间的整数。
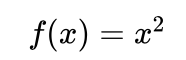
前面我们已经介绍了该问题如何编码、以及具体的选择、交叉和变异操作,这里直接引用前面的结果,将注意力主要关注在遗传算法的具体求解过程。
(1)编码。用5位二进制进行编码,如00000表示x=0,10101表示x=21,11111表示x=31等。其中的0、1为基因。
(2)适应函数。用f(x)作为适应函数,F(x)=f(x)。
(3)初始参数。假设群体的规模N=4,交叉概率 pc=100% ,变异概率pm = 1%。设随机生成的初始群体为:
01101,11000,01000,10011
(4)选择方法。采用“确定性”方法。
小明:您曾经提到过,遗传算法中一般要求具有比较大的群体规模,才有利于遗传进化。这个例子中群体规模只有4,是不是有点小啊?
艾博士:这个群体规模确实有点小,这里只是为了举例,以便简化求解过程,才用了一个比较小的群体规模。
表4.8给出了第0代群体的总体情况。
表4.8:第0代情况表
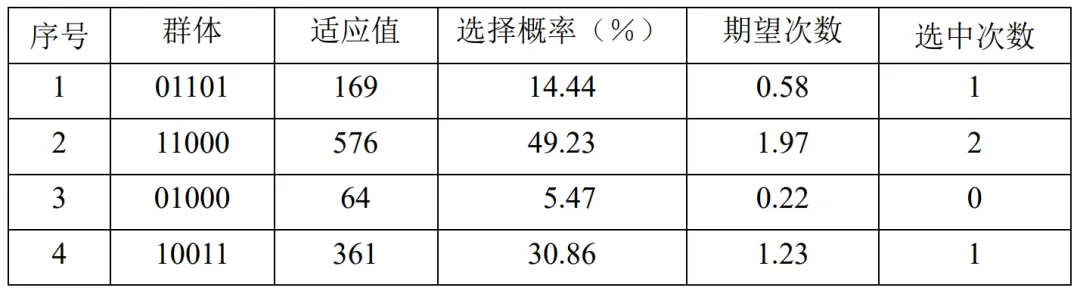
由表4.8我们可以得到,在第0代中,最大适应值为576,最小适应值为64,平均适应值为292.5。我们用 Fm 记录到目前为止得到的最大适应值,用 xm 记录对应的染色体,所以有 Fm=576 ,xm=11000 。
采用“确定性”方法获取选择后的种群。在表4.8中,第二、第四个染色体的期望选择次数整数部分均为1,所以这两个染色体各自被选中一次。由于群体规模为4,需要根据选中次数期望值的小数部分,依次选择两个小数部分大的染色体补充到种群中。这时第二个、第一个染色体被选中期望值的小数部分最大,所以这两个染色体也被选入到种群中。这样第二个染色体11000被选中了两次,第一个染色体01101、第四个染色体10011分别被选中了一次,而第三个染色体由于适应值太小而被淘汰。经选择后得到第0代的种群为:
01101,11000,11000,10011
由于假定了交叉概率为100%,所以种群中的所有染色体均参予交叉操作。我们假定种群中的染色体按顺序两两配对交叉,即第一、第二两个染色体交叉,第三、第四两个染色体交叉,并假定随机产生了交叉位。则交叉后的情况由表4.9给出。
表4.9:第0代种群的交叉情况
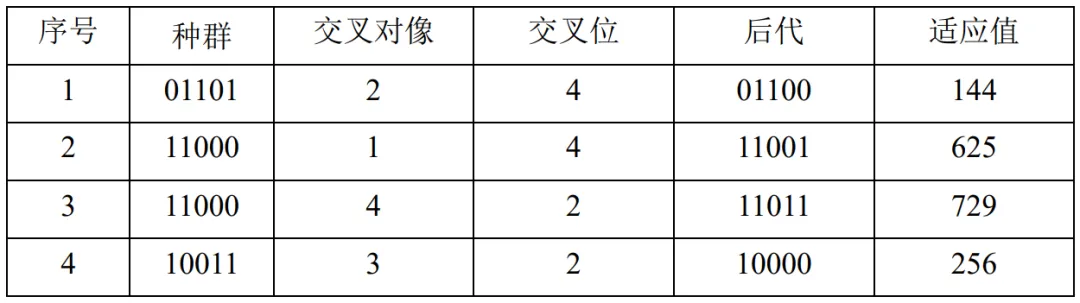
经过交叉操作后得到的新群体为01100,11001,11011,10000。其中最大适应值为729,最小适应值为144,平均适应值为438.5。与第0代群体相比,最大适应值由576提高到729,平均适应值由292.5提高到438.5。由于出现了更大的适应值,所以Fm 、 xm分别修改为Fm=729 、xm=11011 。
由于变异概率比较小,假定在这次循环中没有变异发生,则01100、11001、11011、10000即为进化得到的第1代群体。
表4.10、表4.11给出了第1代群体选择操作和交叉操作之后的情况。第1代群体经交叉操作后虽然平均适应值由438.5提高到584.75,但是最大适应值没有发生任何变化,Fm 、xm 保持不变。
对于这个简单问题来说,我们很容易知道最优解发生在染色体11111,而从得到的新群体11011、11001、10000、11011来看,第三位基因均为0,因此已经不可能通过交叉操作达到最优解了。这种过早的陷入局部最优解的现象称之为早熟。
扩大群体的规模可以防止早熟现象的发生。因此遗传算法一般要求具有一定的群体规模。变异也可以提高群体的多样性,从而为防止出现早熟起到一定的作用。比如,在表4.11的后代中,如果在第二个染色体的第三位发生了变异,则该染色体由原来的11001变为11101,这样就得到了第2代群体:11011,11101,10000,11011。表4.12给出了这种变异的情况,变异之后,适应值最大值又提高到841,Fm 、xm 分别修改为Fm=841 、xm=11101 。
小明:应该如何确定变异位呢?
艾博士:在解决实际问题中,由于问题的复杂性,我们不可能知道变异位应该发生在哪里对我们求解有利。实际问题中的变异位是随机产生的,通过按照一定的概率随机发生变异,提高群体的多样性,通过多样性尽可能避免出现早熟现象。
表4.10:第1代情况表
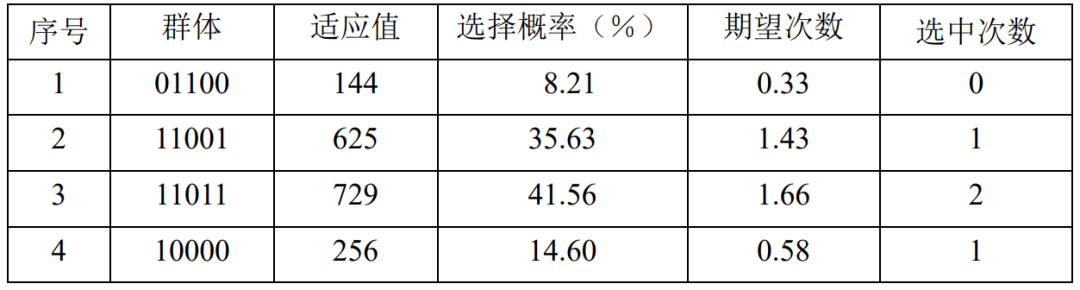
表4.11:第1代种群的交叉情况
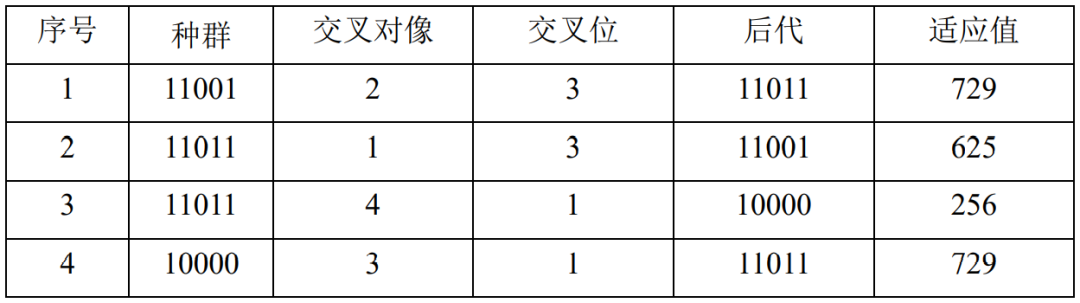
表4.12:第1代变异情况
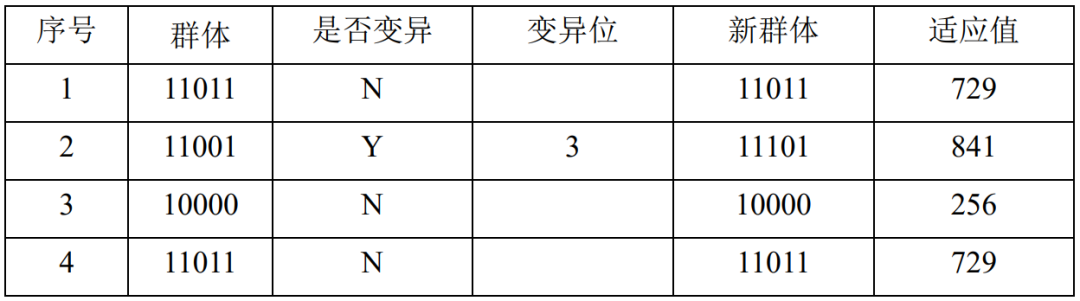
表4.13:第2代情况表
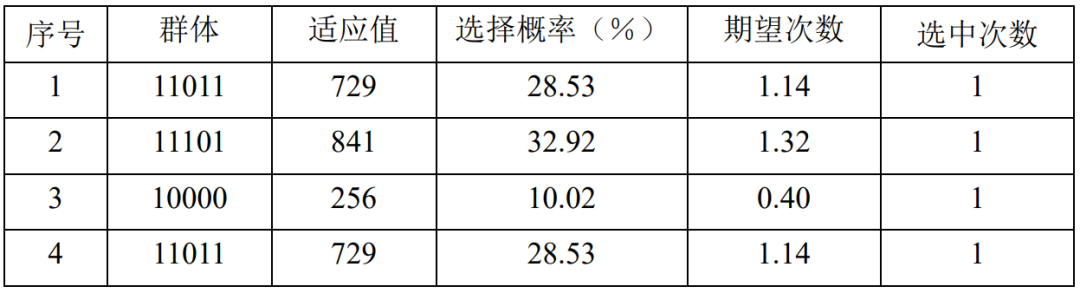
表4.14:第2代种群的交叉情况
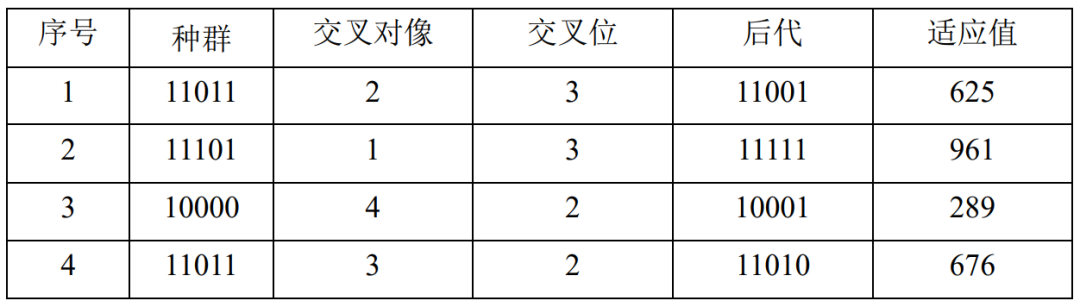
表4.13、表4.14给出了第2代群体选择操作和交叉操作之后的情况。得到了第3代群体:11001、11111、10001、11010。其中平均适应值为637.75,得到了新的适应值最大值961, 、 分别修改为 、 。
图4.15. 生物进化圈示意图
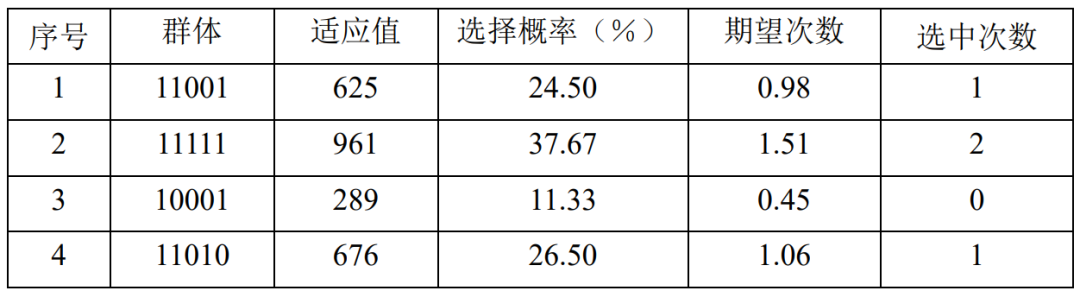
表4.16:第3代种群的交叉情况
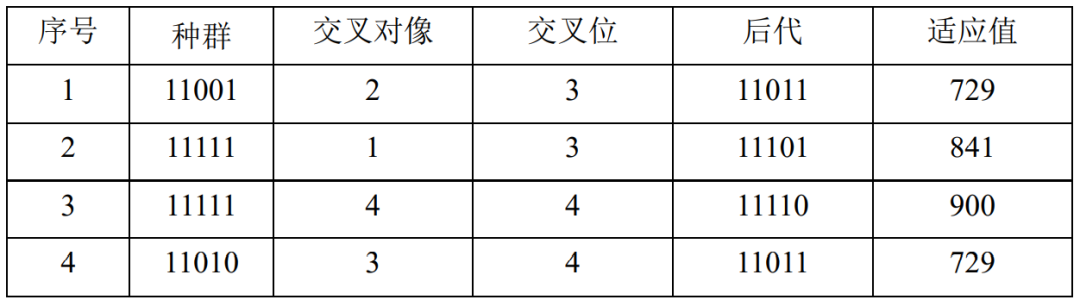
表4.15、表4.16给出了第3代群体选择操作和交叉操作之后的情况。得到了第4代群体:11011、11101、11110、11011。其中平均适应值为799.75,到目前为止的适应值最大值仍然是961,Fm 、xm 保持不变,分别是Fm=961 ,xm=11111 。
艾博士:假定遗传算法到此结束,小明请你说说,算法应该输出什么结果?
小明想了想说:艾博士您前面强调过,遗传算法应该输出进化过程中得到的最大适应值对应的个体。在这个例子中,Fm 保存的就是进化过程中的适应值最大值961,其对应的染色体是 xm ,也就是11111。将其解码后我们就得到了遗传算法的输出,即编码11111对应的x取值31。这应该就是算法的输出结果,x为31,求得的最大值为961。
艾博士:小明说的是对的。在遗传算法中,输出的不是最后一代中的最好结果,而是进化过程中的最好结果,必须牢记住这一点。
小明:在这个例子中,第2代结束时就得到了这个问题的最大值,为什么这时不结束算法,而是继续遗传下去呢?
艾博士:对于实际问题来说,我们事先并不知道最大值是多少,所以也就无从判断什么时候得到了最大值。关于遗传算法什么时候结束的问题,目前还没有有效的判定方法,一般可以通过规定进化的最大代数来定义,在达到了指定的进化代数后,算法停止。或者定义为经过连续的几代进化后,得到的最优解没有任何变化算法停止。
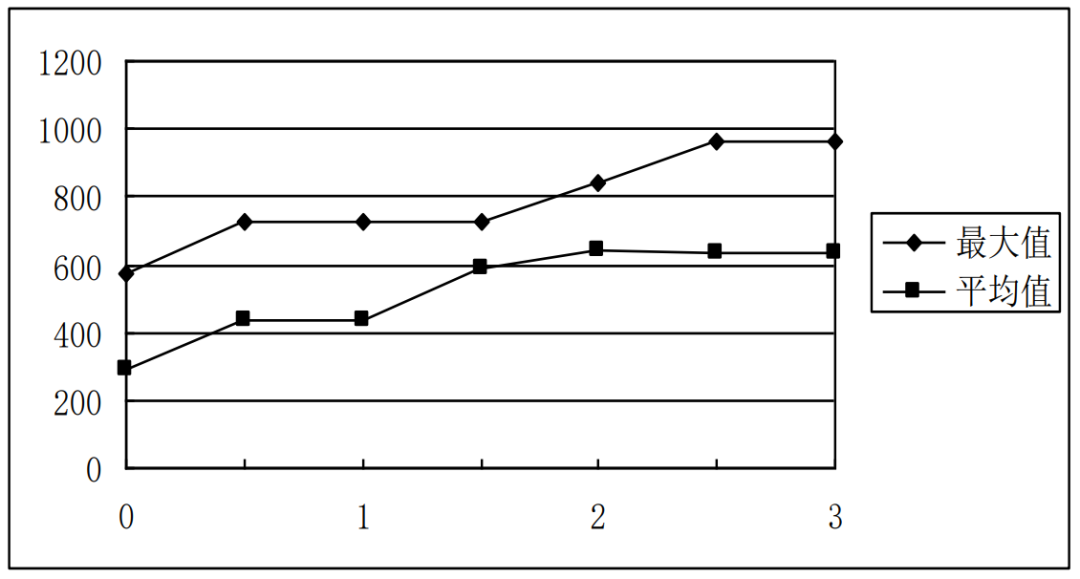
图4.19 最大适应值、平均适应值进化曲线
图4.19给出了该例题的最大适应值和平均适应值随进化过程的变化情况。其中纵坐标是适应函数值,横坐标是进化代数,代与代之间的一个点是交叉后的结果。从图中可以看出,无论是最大适应值还是平均适应值,均随着进化的进行呈上升趋势。我们也可以通过观察该进化曲线判断算法是否可以结束了,如果曲线变化基本处于平稳了算法就可以结束了,否则就需要继续运行下去。
小明:这个例子通俗易懂,详细地说明了遗传算法的各个过程,对于了解遗传算法很有帮助。艾博士,我想知道遗传算法找到的解的质量如何?能否保证找到最优解?
艾博士:和模拟退火算法一样,遗传算法属于随机算法,每次运行结果可能是不一样的,并不能保证每次都可以得到最优解。但是在一定条件下,遗传算法和模拟退火一样,可以以概率1收敛到最优解。下面这个定理说明了这一点。
定理:如果在代的进化过程中,遗传算法每次保留到目前为止的最好解,并且算法以交叉和变异为其随机化操作,则对于一个全局最优化问题,当进化代数趋于无穷时,遗传算法找到最优解的概率为1。
该定理从理论上保证了只要进化的代数足够多,则遗传算法找到最优解的可能性会非常大。在实际使用中,由于要考虑在可接受的有限时间内算法的停止问题,因此解的质量与算法的参数,如群体的规模、交叉概率、变异概率和进化代数等有很大的关系。这些与遗传算法实现紧密相关的参数选取问题我们将在下一节讨论。
讲到这里艾博士总结说:通过以上介绍,我们可以总结出遗传算法具有如下几个特点:
(1)遗传算法是一个随机搜索算法,适用于数值求解具有多参数、多变量、多目标等复杂的最优化问题。
(2)遗传算法对待求解问题的指标函数没有什么特殊的要求,比如不要求诸如连续性、导数存在、单峰值假设等。甚至于不需要显式的写出指标函数,只要能计算就可以。
(3)在经过编码以后,遗传算法几乎不需要任何与问题有关的知识,唯一需要的信息是适应值的计算。也不需要使用者对问题有很深入的了解和求解技巧,通过选择、交叉和变异等简单的操作求解复杂的问题,是一个比较通用的优化算法。
(4)遗传算法具有天然的并行性,交叉、变异等操作都可以并行进行,适用于并行求解。
小明读书笔记
通过一个求解最大值的例子,给出了遗传算法的详细求解过程,可以更好地理解什么是遗传算法。
未完待续

