第四篇 如何用随机算法求解组合优化问题（七）

清华大学计算机系 马少平

第七节：模拟退火算法应用举例

小明：艾博士，我们讲了这么多的方法，请您介绍一个具体的应用例子吧。

艾博士：好的，下面就以旅行商问题为例，看看如何利用模拟退火算法求解该问题。

例：旅行商问题

设有n个城市，城市间的距离用矩阵 D＝[dij](i,j=1,2,...,3) 表示，其中 dij 表示城市i与城市j之间的距离。有一个旅行商从一个城市出发，每个城市访问一次，并且只能访问一次，最后再回到出发城市。问如何行走才能使得行走的路径长度最短。

下面我们讲解一下用模拟退火算法求解旅行商问题需要确定的几个问题。

（1）解空间

艾博士：我们首先分析一下旅行商问题的解空间有多大，以便了解该问题的求解难度。n个城市的任何一种排列 (π1,...,πn) 均是问题的一个可能解。其中πi ＝ j(j=1,2,...,n)表示第i个到达的是城市j，并且默认 πn+1=π1 ，也就是最后要返回到出发城市。解空间的规模也就是所有可能的行走路线共有n!个，当城市数为10时，解的规模为10！=3628800。如果说这个规模还可以通过穷举方法求解的话，则当城市数为20时，解的规模约为 20!≈2.43*10^18 ，据估算在10亿次/秒的计算机上把所有的路径都穷举一边的话，大约需要77年时间，这时就完全不可能通过穷举的办法求解了。

小明：这个数量确实有些吓人啊。

（2）指标函数

艾博士：利用模拟退火算法求解组合优化问题，首先要确立一个指标函数。由于旅行商问题本身要求解最短长度的行走路径，很自然可以选用访问所有城市的路径长度为问题的指标函数。即：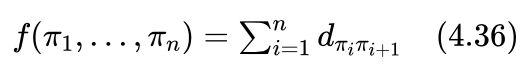
      

需要注意的是，这里默认 πn+1=π1 ，因为最后要返回到出发城市。

（3）新解的产生

艾博士：需要确认的第二个问题是如何从当前解产生一个新解，也即邻居。这里我们采用前面曾经介绍过的逆序交换法，随机选中两个城市，然后将两个城市之间的城市进行逆序交换的方式得到一个新解。具体如下：

设当前解是(π1,...,πn) ，随机选中的两个城市为第u个和第v个到访的城市，假设u<v，u≥0，v≤n+1。则逆序排列u和v之间的城市，得到问题的新解为：

(π1,...,πu,πu-1,...,πu+1,πv,πv+1,...,πn) (4.37)

小明：这里的u和v为什么取值范围是u≥0、v≤n+1？解序列 (π1,...,πn) 中，表示城市的下标是从1到n啊？为什么会有u≥0、v≤n+1呢？

艾博士：很高兴小明注意到了这个问题，这是初学者很容易犯的一个错误。由于这里产生新解的方法是对u、v之间的城市进行逆序交换，并不包含u、v两个城市，所以如果u不包含0、v不包含n+1的话，就会将这个解序列的第一个城市 π1 和最后一个城市 πn 固定住，永远得不到交换。对于第一个城市 π1 还好，因为是出发城市，即便固定住也没有关系，但是对于最后一个城市 πn 是不能固定在最后一个位置的，除非最优解πn  就是在最后一个位置。

小明：我明白了。但是如果u含有0的话，就有可能把第一个城市交换到其他位置了，这样出发城市不就变了吗？

艾博士：由于这n个城市是循环连接在一起的，即便出发城市换了位置也没有关系，当得到最优解之后，再从出发城市开始转一圈就可以了。比如假设算法求得的最佳路径是B-E-A-D-C，而A是出发城市，可以得到路径A-D-C-B-E。

小明恍然大悟到：确实是这样啊，因为路径是循环的，具体哪个城市在第一个位置并不重要。

艾博士：由于路径是循环的，所以在用逆序方法获得新解时，也不一定要求u<v，当uv时，则交换u之后到v之前的城市。

如图4.13、图4.14所示，给出了这两种交换的示意图。在实际编程实现时，我们采用了第二种方法，取得了比较好的应用效果。

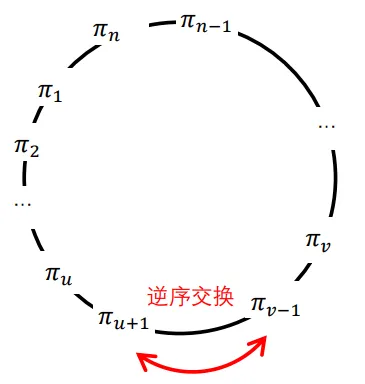
图4.13 当u<v时，逆序交换u、v之间的城市

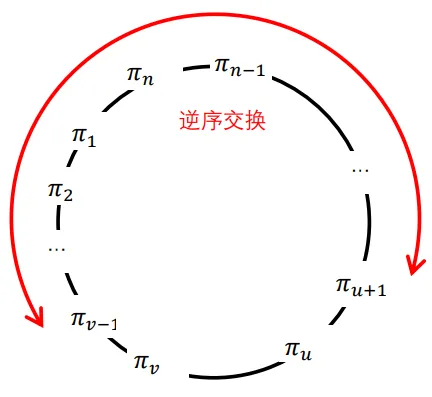
图4.14 当u>v时，交换u之后到v之前的城市

小明：这两个图很形象地示给出了逆序交换法的求解方法，更容易理解了。实际上由于路径是循环的，所以无论是u比v大还是u比v小，都可以看做是从u的下一个城市到v之前的城市之间做逆序交换。

艾博士肯定地说：对，就是这样的。

（4）指标函数差

艾博士：在模拟退火算法中，当解i的指标函数值f(i)大于解j的指标函数值f(j)时，则温度t下从i到j的被接受概率 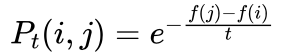 ，这里需要计算i、j两个解间的指标函数差。对于旅行商问题来说，当然可以分别计算出两个解对应的路径距离再相减得到。但是当我们采用逆序交换方法产生新解时，可以更简单地计算出两个解对应路径距离的差值。

小明：如何地计算出两个解对应路径的距离差呢？

艾博士：设当前解i为：

经逆序交换后得到的新解j为：

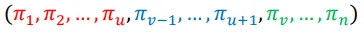
对比上述两个解，红颜色和绿颜色部分的局部路径是一样的，其路径长度也一样。蓝颜色部分的局部路径只是方向不一样，一个是从 πu+1 到 πv-1 ，一个是反过来从  πv-1到   πu+1，但是相邻的城市都是一样的，所以这部分的路径长度也是一样的。所以在计算f(j)-f(i)时，这三段路径长度会被抵消掉，不同的地方只是发生在颜色变化的交界处。在解i中  πu, πu+1、πv-1,πv 两处连接，在解j中变成了πu,πv-1 、πu+1,πv 。所以在计算f(j)-f(i)时，只需考虑这4处不同的地方就可以了。所以有：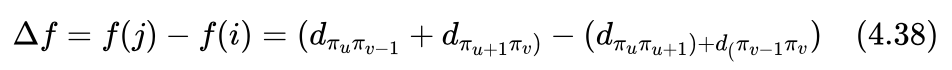

其中 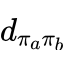 表示 πα、πb 两个城市之间的距离。

这样按照Metropolis准则，在温度t下从解i到j解的接受概率为：

小明：这样一来确实简化了计算。

（5）其他参数的确定

艾博士：还有几个参数需要确定。这个问题我曾经编写过程序，做过一些对比实验，实验中采用的参数如下：

初始温度 t0 我们设置为200；温度衰减系数α=0.95，也即按照等比例下降的方式降温tk+1=αtk+1  ；每个温度下的迭代次数为100n，其中n为城市数；最后算法的结束条件采用无变化控制法，也即当算法连续得到的n个解无任何变化时算法结束。通过多次测试发现，当n=2时就可以得到很好的效果。

讲到这里艾博士对小明说：有了以上内容，就可以编写一个程序用模拟退火算法求解旅行商问题了。作为练习，请小明写一个程序吧。

小明说：好的，我这就去写程序。

小明很快完成程序编写，问艾博士：请问有具体的旅行商问题的例子吗？我测试一下写的程序是否正确。

艾博士从书柜里拿出一本Nirwan Ansari和Edwin Hou两人合写的的《用于最优化的计算智能》，对小明说：小明，这本书中给出了两个例子，分别是10城市和20城市的旅行商问题，你可以用于测试。

小明接过书，从中找到了这两个例子，分别如表4.3和表4.4所示。

艾博士解释说：表中分别给出了10个城市和20个城市的坐标，英文字母表示城市名，任何两个城市之间的距离按照欧氏距离通过城市坐标计算。

表4.3 10城市旅行商问题

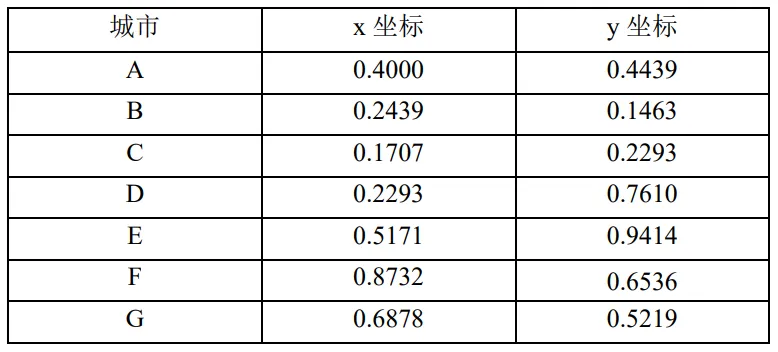
表4.4：20城市旅行商问题

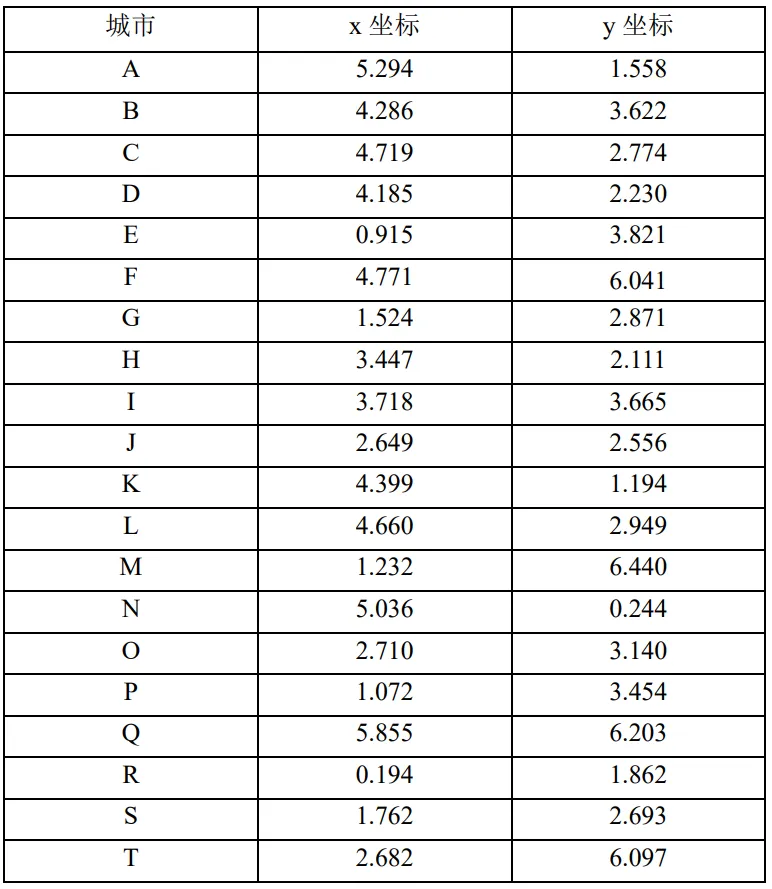
艾博士：Nirwan Ansari和Edwin Hou两人在书中给出了一组参数如下：

初始温度t0是采用升温的方法获得，具体方法为：从 t0=1 出发，并以 t0=1.05t0 对 t0 进行升温，直到接受概率大于0.9时为止，此时得到的温度为初始温度 t0 ；

在每个温度下采用固定的迭代次数 Lk=10n ，其中n为城市数；

温度的衰减系数 α＝0.95 ，即 tk+1=0.95tk ；

算法的停止准则为温度低于0.01时结束。

艾博士进一步说明到：采用这样的参数，书中给出的求解结果如表4.5、表4.6所示。表中的出现次数是1000次运行中出现该结果的次数，平均转移次数是每次运行中状态被接受的平均转移次数，路径是城市的访问次序，路径长度是该路径的长度。最差解指的是1000次运行中得到的最差结果。

对于10城市旅行商问题，在1000次运行中，共有906次求得了最优解，得到最优解的有效解答率为90.6％，平均转移次数为3952次。

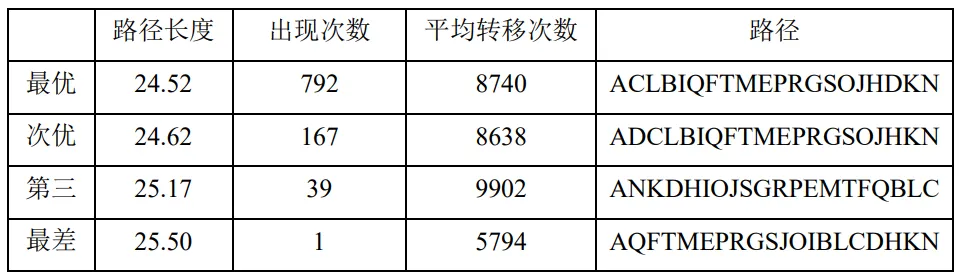
对于20城市旅行商问题，在1000次运行中，共有792次求得了最优解，得到最优解的有效解答率为79.2％，平均转移次数为8740次。

从两个表中可以得出这样的结论，模拟退火算法求解旅行商问题还是非常有效的，大多数情况下都能找到最优解结束，即便不是最优解，也是一个可以接受的满意解，即使是最差的结果，与最优解的差距也不是很大。

表4.5：10城市旅行商问题求解结果

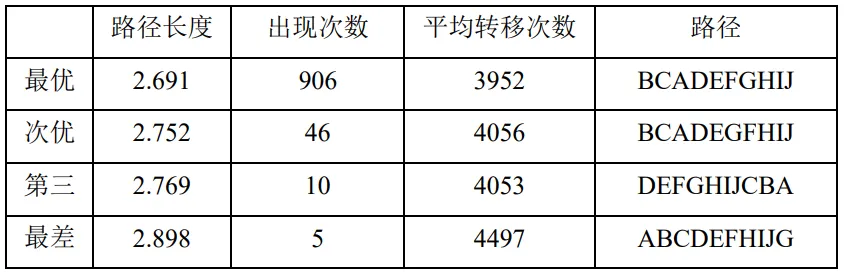
表4.6：20城市旅行商问题求解结果

小明：看起来这个结果很好啊，从产生的平均转移次数看，求解速度也应该是很快的。

艾博士：是这样的，我曾经编程实现过这个程序，速度非常快，基本上是瞬间就出来结果。前面讲解中向你提供的一些参数的设置建议，就是我具体编程实现时采用的参数。你可以运行一下你的程序，跟这本书中提供的结果做一个对比。

像书中一样，对于10城市和20城市小明分别将程序循环运行1000次，记录每次的运行结果。程序运行的确实非常快，即便是循环运行1000次，也很快就结束了。

刚一看到结果，小明就惊呼起来：不会吧？怎么1000次运行中每次都得到了最优解？效果会这么好吗？

艾博士说：确实是这样的，我写的程序也是这个结果。在确定具体参数时，除了参考了Nirwan Ansari和Edwin Hou两人在书中给出的参数外，我还参考了康立山等人编写的《演化计算》一书中给出的参数设置。该书给出的参数设置为：

初始温度 t0=280 ；

在每个温度下采用固定的迭代次数 Lk=100n ，其中n为城市数；

温度的衰减系数 α＝ 0.92，即 tk+1=0.92tk ；

算法的停止准则为：当相邻两个温度得到的解无任何变化时算法停止。

综合参考上述两本书，经多次实验、反复调试、对比、修改之后，才最终得到了现在的参数设置，即便效果好一些，也是因为参考了别人的方法。

小明：看来做什么都不能闭门造车，要在别人工作的基础上总结提高。

小明读书笔记

以旅行商问题为例，详细讨论了模拟退火算法的具体实现问题。包括指标函数的选择，新解的产生，初始温度的设定，温度下降方法，同一温度下的循环次数，以及算法的结束条件等。结合两个具体例子——10城市和20城市旅行商问题，对运行结果进行了分析。

未完待续