第三篇 计算机是如何找到最优路径的(四)下
清华大学计算机系 马少平
第四节:启发式搜索
5、A*算法存在的不足
艾博士:A*算法体现出了很好的性能,也是人工智能研究领域一个重要的算法。但是A*算法也存在一些不足。
小明:A*算法存在哪些不足呢?
艾博士:小明,请说说A*算法中,当产生的节点已经在CLOSED中时是如何处理的?
小明想了想回答说:对于从节点n产生的节点 mi ,如果 mi 已经在CLOSED中,则要比较通过n产生 mi 计算的 f(n,mi) 与以前得到的 f(mi) 之间的大小,当 f(n,mi) 小于f(mi) 时,说明通过n到 mi 这条路径代价更小。按照A*算法,这时要将 mi 从CLOSED中取出,重新放回到OPEN中。
艾博士对小明的回答非常满意:回答的很对,看来是认真复习了。
mi 在CLOSED中,说明节点 mi 之前已经被扩展过,现在又将 mi 重新放回到OPEN中,那么 mi 就有可能被再次扩展,也就是说存在同一个节点被重复扩展的可能。如果有多个节点反复被重复扩展,显然就降低了A*算法的搜索效率。
我们看一个例子。假设某问题状态连接图如图3.19所示。其中字母旁括号中的数字表示该节点的h值,连线边的数字表示两个节点间的代价。图3.20给出了以OPEN、CLOSED表示的搜索过程,字母后面括号中的数字为该节点的f值,当算法结束时,找到了从S到T的最佳路径S-C-B-A-T。
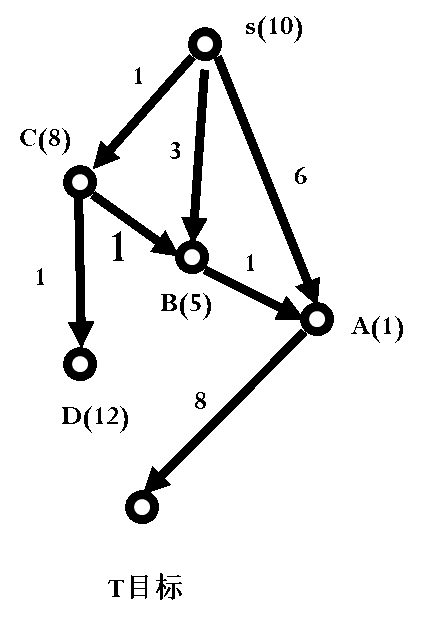
图3.19 某问题状态连接图
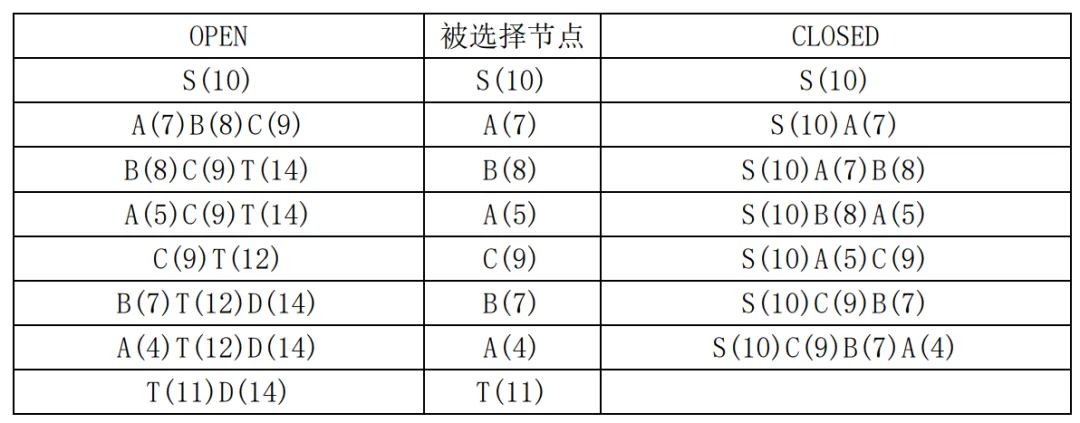
图3.20 图3.19所示问题的搜索过程
艾博士:我们来分析一下这个问题的搜索过程。
开始时OPEN表中只有一个初始节点S(10),扩展S产生节点A(7)、B(8)、C(9),这三个节点的父节点均为S。节点A(7)的f值最小,被从OPEN中取出扩展,产生子节点T(14)放入到OPEN中,节点A(7)被从OPEN中删除放入到CLOSED中。这时虽然已经找到了一条从初始节点S到目标节点T的路径S-A-T,但是由于目标节点T没有排在OPEN的第一个位置,继续搜索。从OPEN中取出第一个节点B(8),产生子节点A,由于节点A已经在CLOSED中,而通过节点B新产生的节点A的f值为5,小于之前A的f值7,所以将节点A从CLOSED中删除,重新放回到OPEN中,节点A的f值修改为5,其父节点修改为节点B。节点A(5)再次被排在OPEN的第一个位置,从OPEN中取出放入到CLOSED中,产生子节点T。节点T已经在OPEN中了,到达T的新路径f值为12,小于之前的f值14,修改T的f值为12,仍然在OPEN中。经排序后,C(9)在OPEN的第一个位置,从OPEN中取出C(9)放入到CLOSED中,扩展节点C(9)产生节点B(7)和节点D(14)。节点D(14)是新节点,直接放入到OPEN中,标记其父节点为节点C。B(8)节点已经在CLOSED中,而通过节点C产生的节点B的f值为7,小于之前的f值8,所以B被从CLOSED中取出放回到OPEN中,B以7的f值又排在了OPEN中第一个位置,其父节点也被修改为节点C。B(7)被从OPEN中取出,放入到CLOSED中,扩展节点B(7)再次产生节点A(4),而节点A(5)在CLOSED中,到达A的新路径f值为4,小于之前路径的f值5,所以A被重新放回到OPEN中,以f值4又一次排在了OPEN的第一个位置。节点A(4)再次被扩展,产生节点T(11)。节点T已经在OPEN中,到达节点T的新路径的f值11小于之前的f值12,修改节点T的f值为11。OPEN表经重新排序后,节点T排在了OPEN的第一个位置,当节点T被从OPEN中取出后,发现T就是目标节点,所以算法结束,找到了从初始节点S到目标节点T的路径为S-C-B-A-T,路径长度为11。
讲解完这个例子的搜索过程之后艾博士问小明:从图3.20给出的搜索过程看出什么问题吗?
小明:在听您的讲解过程中,就发现节点A和B被多次从CLOSED中取出重新放回到OPEN中,导致这两个节点被反复扩展多次,节点A被重复扩展了3次,节点B被重复扩展了2次。为什么会出现这种情况呢?
艾博士:小明观察的很仔细,该例子说明,A*算法确实存在一个节点被多次重复扩展的情况发生,这就是我们要讨论的A*算法存在的不足,将影响算法的搜索效率。
之所以会出现这样的问题,是因为如果到达一个节点存在多条路径,而第一次扩展时找到的不是到达该节点的最短路径,那么在后续扩展中该节点就有可能被多次扩展。以该例子为例,由于节点A是从初始节点S到达目标节点T的必经之路,A*算法为了找到到达目标节点T的最优路径,必然会多次扩展节点A,直到寻找到了从S到达A的最短路径,这样才有可能搜索到到达目标节点T的最短路径。
小明:那么出现这种情况的原因是什么呢?
艾博士:这是由于h函数设计不合理带来的问题。因为A*算法只要求对于任何节点n满足h(n)≤h*(n)即可,并没有其他方面的要求。
6、单调的h函数
小明:我们是否还可以对h函数增加其他方面的限制呢?
艾博士:我们先来讨论一下一个合理的h函数应该满足什么样的条件。我们设想,当你距离一个目标比较近时,估计的到目标的距离会比较准确,而当距离目标比较远时,估计的到目标的距离误差会大一些。也就是说,距离目标越远,估计的距离误差越大,而距离目标越近,估计的距离误差越小。如果我们要求h函数满足这样的要求,应该是一个合理的限制条件。反之,如果定义的h函数如果距离目标比较近时估计的误差反而更大,则说明该h函数定义的不太合理。
小明:感觉这个要求是合理的,距离目标越近应该越容易估计,也就应该估计的越准确。
艾博士:由于h*(n)是节点n到达目标节点T最短路径的真实代价,而h(n)是h*(n)的估计值,所以h(n)的估计误差可以表示为:
h*(n)-h(n)
设 ni 是 nj 的父节点,ni 、nj 之间的代价用 C(ni,nj)表示。当nj比ni更接近目标节点时,按照上述限制条件,应该有:
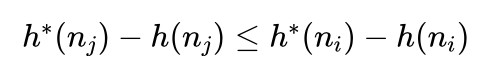
整理有:
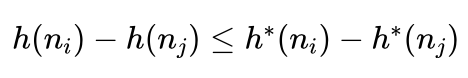
如果nj在节点ni到目标节点T的最短路径上,则:
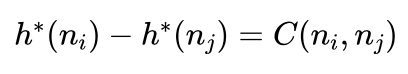
所以:
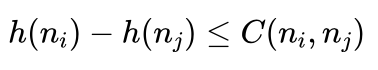
如果 nj 不在节点 ni 到目标节点T的最短路径上,说明 ni 经过 nj 到达目标节点T的最短路径代价 C(ni,nj)+h*(nj) 要大于节点 ni 到目标的最短路径代价 h*(ni) ,因此有:
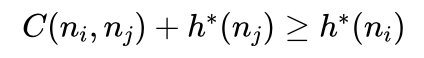
所以:
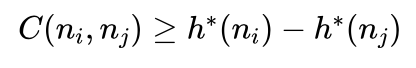
同样有:
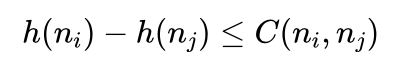
所以满足“距离目标越远,估计的距离误差越大,而距离目标越近,估计的距离误差越小”的必要条件就是满足不等式条件: 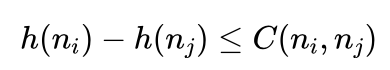
h*(T) 表示的是目标节点T到自己的最佳路径代价,所以有 h*(T)=0 ,因此我们可以再加上一个条件,要求:
h(T)=0
整理一下,我们认为h函数一个更合理的条件是满足以下的限制条件:
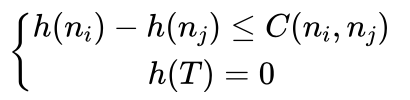
我们称该条件为单调条件,满足该条件的h函数称作是单调的。
小明:当h函数满足单调条件时,有什么好处呢?
艾博士:对于满足单调条件的h函数,我们有如下定理:
若h函数满足单调条件,则A*选择一个节点扩展时,就找到了到达该节点的最优路径,即:此时有 g(n)=g*(n) 。
小明看完该定理的描述,马上高兴地说:艾博士,我明白了。前面说之所以A*算法会出现重复扩展节点问题,就是因为A*算法第一次扩展一个节点时,找到的不一定是到达该节点的最优路径。而该定理说:如果h函数满足单调条件,A*选择一个节点扩展时,就找到了到达该节点的最优路径。这样的话,如果h函数满足单调条件,A*算法就不会出现重复扩展节点的问题了。
艾博士夸奖到:小明分析的非常正确,只要h函数是单调的,则A*算法一定不会出现重复扩展节点问题。因为第一次扩展就找到了到达该节点的最优路径,那么后续即便又发现到达该节点的其他路径,其f值也不可能小于第一次找到的路径的f值,所以就不会出现将该节点从CLOSED中取出重新放回到OPEN中的情况发生,也就不会出现重复扩展节点的问题了。
小明:是这个道理。那么如何判断一个h函数是否满足单调条件呢?
艾博士:这需要结合具体问题判定是否满足单调条件。
比如八数码问题h函数定义为“不在位的将牌数”,假设移动一次将牌的代价为1,则:
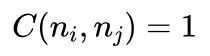
从父节点 移动一个将牌到子节点 ,可能出现的情况共有如下三种:
将一个不在位的将牌移动到位了,则不在位将牌数减1;
将一个在位的将牌移动不在位了,则不在位将牌数加1;
一个不在位的将牌移动后仍然不在位,则不在位将牌数不变。
对这三种情况,分别有:
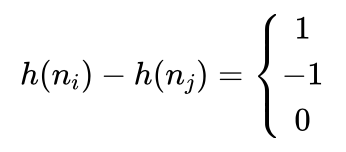
均满足条件:
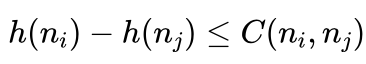
同时由于目标节点不在位将牌数为0,所以满足:
h(T)=0
从而说明以“不在位的将牌数”定义的h函数满足单调条件。
艾博士提醒小明说:在判断是否满足单调条件时,一定不要忘记h(T)=0这个条件,这也是初学者容易忘记的。
艾博士:我们再看图3.19所示的例子,对于A、B两个节点,B是A的父节点,图中给出了h(B)=5,h((A)=1,C(B,A)=1。带入单调条件中,有:
h(B)-h(A)=5-1=4>C(B,A)=1
不满足h函数的单调条件,所以出现了节点被多次重复扩展的问题。
小明又问艾博士:在介绍h函数的单调条件时,并没有明确说h函数是否满足A*条件,需要加上这个条件吗?
艾博士:小明真是一个好学的聪明孩子,总是能提出一些关键问题。可以证明,满足单调条件的h函数一定满足A*条件,所以就不需要再加上A*条件了。
小明:明白了。只要是满足单调条件的h函数,就一定满足A*条件。相反,满足A*条件的h函数,不一定满足单调条件。
艾博士:是这样的。最后我再说一下如何记忆单调条件。
如图3.21所示,节点 nj 是节点 ni 的父节点,T是目标节点,图中虚线表示 h(ni) 、h(nj) ,可以看成是一个三角形的两个边,而 ni 、nj 之间的代价 C(ni,nj) 可以看成是三角形的另一个边。这样h函数的单调条件 h(ni)-h(nj)<=C(ni,nj) 刚好满足三角不等式。

图3.21 单调条件与三角不等式关系示意图
小明对照着图和单调条件说:果然是这样的,这真是一个好办法,对照着三角不等式更方便记忆了。
艾博士提醒说:但是千万不要忘记,单调条件还有另一个条件h(T)=0,只有在这种情况下才可以从h函数满足单调条件推导出也满足A*条件。
小明回答说:谢谢艾博士提醒,我记住了。不过我还有一个问题,为什么满足这样条件的h函数被称作是单调的?这里单调的含义是什么?
艾博士解释说:可以证明,当h函数满足单调条件时,A*算法选择扩展的节点序列,其f值是单调非减的,也就是说,在后面扩展的节点的f值一定不会比前面扩展的节点的f值小,f值只会是越来越大或者相等,不可能出现f值下降的情况。这就是被称作单调h函数的原因。
小明:我明白了,原来是这样的。
7、改进的A*算法
小明:艾博士,通过您的讲解,我明白了当h函数满足单调条件时,可以保证A*算法不会出现重复扩展问题。但是,如果因为问题比较复杂,我们定义不出满足单调条件的h函数,是否有办法解决节点重复扩展问题呢?
艾博士:这种情况下我们也可以通过修改A*算法来解决这个问题,不过不能从根本上彻底解决。也就是说,改进后的A*算法比原始的A*算法可以减少重复节点扩展问题,但并不能从根本上避免这个问题,只是减少了重复节点扩展的可能性。这就是下面我们将要介绍的改进的A*算法。
小明迫不及待地问到:怎么改进的呢?请您给讲讲。
艾博士:首先我们确定算法改进的原则:一是不要多扩展节点,因为我们减少重复扩展节点的目的就是为了提高算法的搜索效率,如果为了减少重复节点而多扩展了其他节点,将会得不偿失。二是不要额外增加算法的计算量。要在这两个原则下对A*算法进行改进。
为此,我们先介绍A*算法的两个性质,这是A*算法改进的理论基础。
性质1:在A*算法结束之前,OPEN中任何满足f(n)<f*(S)的节点n,一定会被A*扩展。其中f*(S)表示从初始节点S到目标节点T最短路径的代价。
性质2:A*选作扩展的任何节点n,一定满足f(n)≤f*(S)。
关于单调性,我们再增加一个性质:
性质3:恒等于0的h函数满足单调性质。
听到艾博士介绍到性质3,小明有些不解地问:既然恒等于0的h函数满足单调性质,为什么我们还要费力定义h函数呢?直接取0不就可以了?还可以避免重复节点扩展问题。
艾博士解释说:A*算法的目的就是尽可能地减少扩展节点,恒等于0的h函数虽然满足单调条件,但是缺少必要的启发信息,会多扩展很多节点。所以还是要尽可能地定义h函数。
小明:我明白了,恒等于0的h函数虽然满足单调条件,但是缺乏启发信息。
艾博士接着讲解说:在A*算法中,OPEN中的节点是按照f值从小到大排列好的,根据f*(S)的值可以将OPEN划分为前后两部分:前一部分为f值小于f*(S)的节点,为了表述方便我们将这部分节点放在NEST中。后一部分为f值大于等于f*(S)的节点。如图3.22所示。

图3.22
根据性质1,在NEST中的节点是肯定被A*算法扩展的,既然都被扩展,我们换一个选择扩展节点的策略也不会多扩展节点。
根据性质3,恒等于0的h函数满足单调性质,所以当NEST中有节点存在时,我们可以令这部分节点的h值为0,这样既不会多扩展节点,也可以避免因这部分节点引起的重复扩展问题,也没有额外增加计算量,是不是一个两全其美的方案?
小明听后高兴地说:这可太好了,算法改变并不大,但确实可以避免了重复节点扩展问题。
艾博士提醒小明说:小明,你不要高兴的太早了。
想想看,如果让你按照这个改进的思路写一个程序,这程序能工作吗?
小明听艾博士这么说,就知道这里边一定还存在什么问题,认真地思考起来:艾博士,我明白了,一般来说我们并不知道一个问题的f*(S),所以不能确定哪些节点在NEST中,所以这一改进方案虽然很巧妙,但是并不能解决问题。那可怎么办呢?
艾博士鼓励小明说:小明,也不要沮丧,我们想想有什么解决的办法。A*算法核心思想之一就是估计,h值就是对h*值的估计,我们也可以对f*(S)进行估计,如果能大概估计出f*(S)的值,用这个估计值代替f*(S)就可以了。
小明:这是一个好的想法,但是怎么估计呢?
艾博士:首先f*(S)的估计值不能大于f*(S),因为如果用大于f*(S)的值代替f*(S),NEST就可能存在f值大于f*(S)的节点。根据性质2,这样的节点不会被A*算法扩展,但是按照前面说的改进方案,对NEST中的节点令h值为0,就会被扩展了,会存在多扩展节点的可能,不符合我们前面说的对A*算法进行改进的基本原则。
我们可以这样估计f*(S)的值。根据性质2,被A*选作扩展的任何节点n,一定有f(n)≤f*(S),所以我们可以从已经被扩展的节点中,选一个最大的f值作为f*(S)的估计值,该f值我们记作 。这样,用 代替f*(S)对OPEN中的节点进行划分,确定NEST的节点就可以了。这样确定的NEST,其中的节点可能会少一些,但是也会一定程度地避免一些重复节点的扩展问题。
艾博士:小明,你再想想,这样就否就可以编写程序了?
小明想了想说:应该没有问题了,需要的信息都全了。
艾博士:按照这样的改进思路,我们给出改进的A*算法,该算法与前面介绍的A算法基本一致,主要是增加了一些对NEST的处理。
改进的A*算法:
1、初始化:OPEN=(S), CLOSED=( ),计算f(S), fm =0;
2、循环做以下步骤直到OPEN为空结束:
3、循环开始
4、 将OPEN中f值小于fm 的节点放入到NEST中,
如果NEST中存在节点,则选取一个g值最小的节点作为n,
否则NEST中不存在节点,则从从OPEN中取出第一节点作为n, fm=f(n) ;
5、 如果n就是目标节点,算法结束,回送节点n,算法成功结束;
6、 否则将n从OPEN中删除,放到CLOSED中;
7、 扩展节点n,生成出n的所有子节点,用 表示这些子节点;
8、 计算节点 mi 的f值,由于可能存在多个路径到达 mi ,用 f(n,mi) 表示经过节点n到达 mi 计算出的f值,不同的到达路径其 g(mi) 值可能不同,但是h(mi) 是一样的,因为 h(mi) 是从 mi 到目标节点路径代价的估计值,与如何从初始节点到达 mi 无关;
9、 如果 mi 既不在OPEN中,也不在CLOSED中,则将 mi 加入到OPEN中,并标记 mi 的父节点为n;
10、 如果 mi 在OPEN中,并且f(n,mi) <f(mi) ,则 f(mi)=f(n,mi) ,并标记 mi 的父节点为n;
11、如果 mi 在CLOSED中,并且f(n,mi) < f(mi),则 f(mi)=f(n,mi) ,并标记mi 的父节点为n,将 mi 从CLOSED中删除、加入到OPEN中;
12、 对OPEN中的节点按照f值从小到大排序;
13、循环结束
14、没有找到解,算法以失败结束
改进的A*算法相对于原始算法,只是对第4步做了一些修改。原始算法中是直接从OPEN中取出第一个节点作为n,改进的算法中,先将OPEN表中f值小于fm的节点放入到NEST中。如果NEST中存在节点,则从中选取一个g值最小的节点,也就是相当于h恒等于0后,f值最小的节点,该节点作为n。如果NEST中不存在节点,就同原始算法一样,从OPEN中取出第一个节点作为n。由于f值小于 fm 的节点会被放在NEST中,当NEST中没有节点时,说明OPEN中的节点的f值均大于等 fm ,所以当从OPEN中取出第一个节点n时,f(n)一定是大于等于 fm ,而 fm 记录的又是扩展的节点中最大的f值,所以这时需要用f(n)修改 fm ,即 fm=f(n) ,以维护 fm 为到目前为止扩展的节点中f值的最大值。
讲解到这里,艾博士对小明说:小明,是否学会了改进的A*算法?请你用改进的A*算法求解一次图3.19所示的问题。
小明:好的,我尝试着用改进的A*算法求解,请艾博士看看我做的是否正确。
说完,小明认真地做了起来。
为了方便求解,小明首先重画了图3.19所示的问题如图3.23所示,然后用OPEN、CLOSED的变化情况,给出了该问题的搜索过程,如表3.2所示。
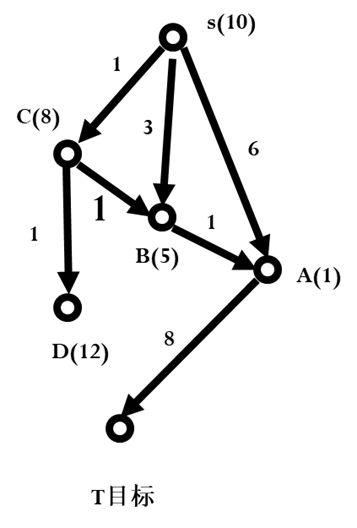
图3.23 某问题状态连接图
表3.2 改进的A*算法求解示例
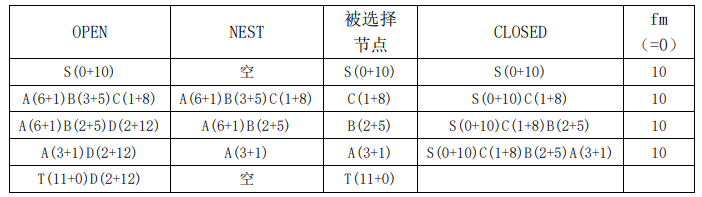
求解完之后,小明开始解释自己是如何求解的:开始的时候,fm 设为0,CLOSED是空的,OPEN中只有S(0+10)一个节点,为了方便求解,这里将g+h在括号中标明。
由于 fm 为0,所以NEST也是空的,算法从OPEN中取出第一个节点S(0+10),从OPEN中删除该节点,放入到CLOSED中,修改 fm 的值为f(S),即10。然后扩展S(0+10),产生节点A(6+1)、B(3+5)、C(1+8),这三个节点均没有在OPEN、CLOSED中出现过,全部放入到OPEN中,设置这三个节点的父节点为S,并按照f值从小到大对OPEN中的节点进行排序。
由于节点A(6+1)、B(3+5)、C(1+8)的f值均小于fm=10 ,所以全部进入到NEST中。从NEST中取出一个g值最小的节点C(1+8),并将其从OPEN中删除放入到CLOSED。扩展C(1+8)产生节点B(2+5)和D(2+12),由于节点B已经在OPEN中,所以需要比较f(C,B)和f(B)的大小。由于f(C,B)=2+5=7,小于f(B)=3+5=8,所以修改f(B)为f(C,B)=7,并修改节点B的父节点为C。节点D直接放入到OPEN中,设置D的父节点为C。对OPEN中的节点重新按f值大小排序。这时OPEN=(A(6+1),B(2+5),D(2+12)),由于A(6+1),B(2+5)两个节点的f值小于 fm ,所以NEST中的节点为A(6+1),B(2+5)。
从NEST中取出g值最小的节点B(2+5),将其从OPEN中删除,加入到CLOSED中,扩展节点B(2+5),产生节点A(3+1)。A已经在OPEN中,由于f(B,A)=4小于f(A)=7,所以将f(A)修改为f(B,A)=4,并修改A的父节点为B。对OPEN中的节点按照f值从小到大排序后有OPEN=(A(3+1),D(2+12)),由于A(3+1)的f值小于 fm ,所以有NEST=(A(3+1))。
从NEST中取出g值最小的节点A(3+1),将其从OPEN中删除,加入到CLOSED中,扩展节点A(3+1),产生节点T(11+0)。节点T是第一次出现的节点,直接加入到OPEN中,并设置其父节点为A。对OPEN中的节点按照f值从小到大排序后,有OPEN=(T(11+0),D(2+12))。由于OPEN中两个节点的f值均大于 fm ,所以这时NEST为空,直接从OPEN取出第一个节点T(11+0),发现T刚好为目标节点,并且其f值是OPEN中最小的,所以算法到此成功结束,输出目标节点T。
艾博士听完小明的介绍补充说:当节点T被从OPEN中取出后,这时T刚好是目标节点,所以算法就结束了。如果这时T不是目标节点,而是另一个节点D,按照改进的A*算法,这时需要用f(D)修改 fm 值,即 fm=f(D) 。当然这种情况并没有发生,因为从OPEN中取出节点T后,发现T是目标节点,算法就结束了。
艾博士补充说明后,问小明:你看还有重复节点扩展问题吗?
小明高兴地说:一次重复扩展节点的情况也没有发生,比起用原始的A*算法求解,效率提高了很多。
艾博士解释说:需要再次强调一下,改进的A*算法并不能保证一定没有重复节点扩展,只是有可能减少重复节点扩展问题。比如在这个例子中,如果S节点的h值修改为9,其他保持不变,如图3.24所示,你再求解一次,看会出现什么情况?
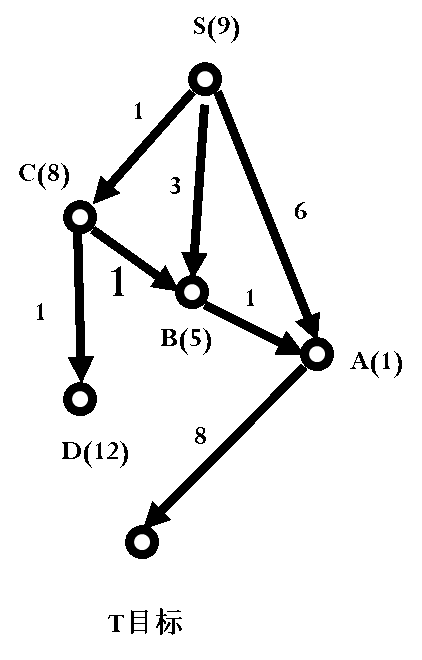
图3.24 某问题状态连接图
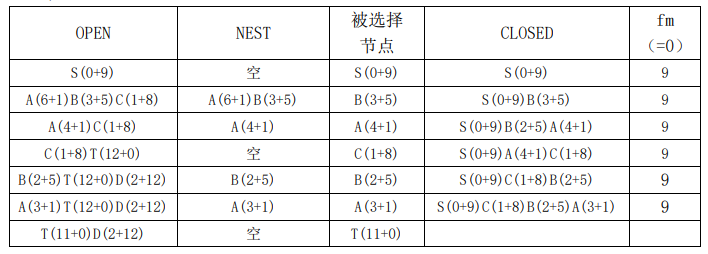
小明又认真做了起来,表3.3给出了搜索过程。从表中可以看出,节点A和B分别被扩展了两次,可见改进的A*算法并不能完全杜绝重复节点扩展问题。
表3.3
小明读书笔记
迪杰斯特拉算法虽然可以找到到达目标节点的最优路径,但是只利用了到达节点的代价,而没有利用节点到目标节点路径的代价,从而导致搜索效率低,产生过多的无用搜索。但是从一个节点到达目标节点的路径一般是不知道的,如何利用该信息呢?A算法采用估计的方法,定义一个启发函数f(n),利用该函数估计节点n到达目标节点路径的代价。
A算法定义评价函数f(n)为:
f(n)=g(n)+h(n)
其中g(n)为从初始节点到节点n的路径代价,h(n)为从节点n到达目标节点路径代价的估计值,f(n)为从初始节点经过节点n到达目标节点路径代价的估计值。
A算法优先选择f值最小的节点扩展,同迪杰斯特拉算法一样,只有当选择扩展的节点为目标节点时算法才结束。
对于任何节点n,当满足条件h(n)≤h*(n)时,A算法称为A*算法,该条件称为A*条件。A*算法可以保证找到路径的最优解。
定义h函数的一般原则:放宽原问题的限制条件,在宽条件下计算从节点n到达目标节点的最短路径,以该路径的代价作为h函数的取值。如何放宽条件与具体问题有关。
当对于同一个问题定义了两个不同的h函数 h1 和 h2 时,如何评价哪个h函数更好呢?如果对于除了目标节点以外的任何节点n,满足 h2>h1,则采用 h2 构成的A*算法扩展的节点一定会被采用 h2 构成的A*算法扩展。因为两个h函数都是满足A*条件的,越大的h函数说明其估计值越准确,所以估计越准确的h函数其效果就越好,至少不会变差。
也可以采用实验的办法,通过计算平均分叉数来评价两个h函数的好坏。平均分叉数越小的h函数,其性能越好。
A*算法存在可能重复扩展节点的问题,影响求解效率。有两个办法解决这个问题,一是定义满足单调条件的h函数,即满足条件:
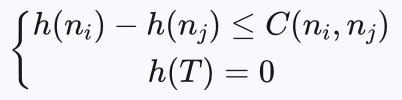
其中T为目标节点,ni 是 nj 的父节点,C(ni,nj) 为节点 ni 到 nj 的代价。当h函数满足单调条件时,就不会出现重复扩展节点的问题。
如果h不满足单调条件时,可以通过改进A*算法的方法,减少重复扩展节点的可能性。
改进的A*算法,设置一个变量 fm ,记录已经扩展节点中最大的f值。当OPEM中存在f值小于 fm 的节点时,将这些节点放入到NEST中。如果NEST不空,则优先从NEST中选择g值最小的节点扩展,如果NEST中没有任何节点,则同A*算法一样,选择OPEN中第一个节点扩展,并用该节点的f值修改 fm 值。其他部分与A*算法完全一样。改进的A*算法可以减少重复节点扩展,但并不保证一定不会出现重复扩展节点问题。
未完待续

