第三篇 计算机是如何找到最优路径的(五)
清华大学计算机系 马少平
第五节:深度优先搜索算法
小明:艾博士,我听说还有一种叫做深度优先的搜索算法?
艾博士:是的,下面我们就介绍一下深度优先搜索算法。小明,请你说说宽度优先搜索算法是如何选择被扩展节点的?
小明想了一下回答说:宽度优先搜索算法优先选择节点深度最浅的节点扩展。
艾博士:小明说的非常正确。与宽度优先搜索算法相反,深度优先搜索算法优先选择深度最深的节点扩展。
小明问:深度优先搜索算法具体是如何实现的呢?
艾博士:深度优先搜索算法有不同的实现方法,一种最常用的实现方法是利用回溯方法实现的。
小明:什么是回溯方法呢?
艾博士:假如我们走迷宫。我们事先规定好某种策略,比如每次遇到路口时,优先选择最左边的路口进入,如果遇到死胡同,则退回来试探第二个路口。当然很多情况下并不是直接就遇到死胡同,而是探索了若干个可能的走法之后才发现进入这个路口是不可行的,这样也相当于遇到了死胡同,退回来再选择其他可能的路口进行试探。这种遇到死胡同就退回的方法称为回溯方法。
为了介绍如何用回溯方法实现深度优先搜索,我们通过四皇后问题的求解,介绍深度优先搜索方法。
小明:请艾博士介绍一下什么是四皇后问题。
艾博士:所谓四皇后问题,就是在一个4×4的棋盘上,如何摆放4个皇后,使得任何两个皇后都不在一条直线上,包括横线、纵线和斜线。比如图3.25所示的就是四皇后问题的一个解,其中“Q”表示皇后。
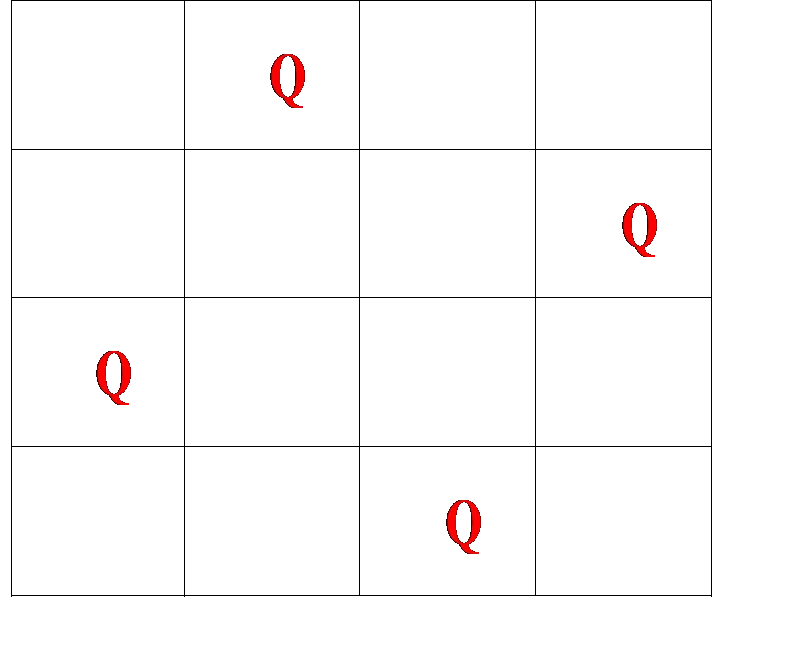
图3.25 四皇后问题
为了叙述方便,我们设棋盘从上到下为第一行、第二行……从左到右为第一列、第二列……我们用棋盘上皇后所在的坐标组成的表表示四皇后问题的一个状态。比如图3.25所示的状态可以表示为:
((1,2), (2,4), (3, 1), (4, 3))
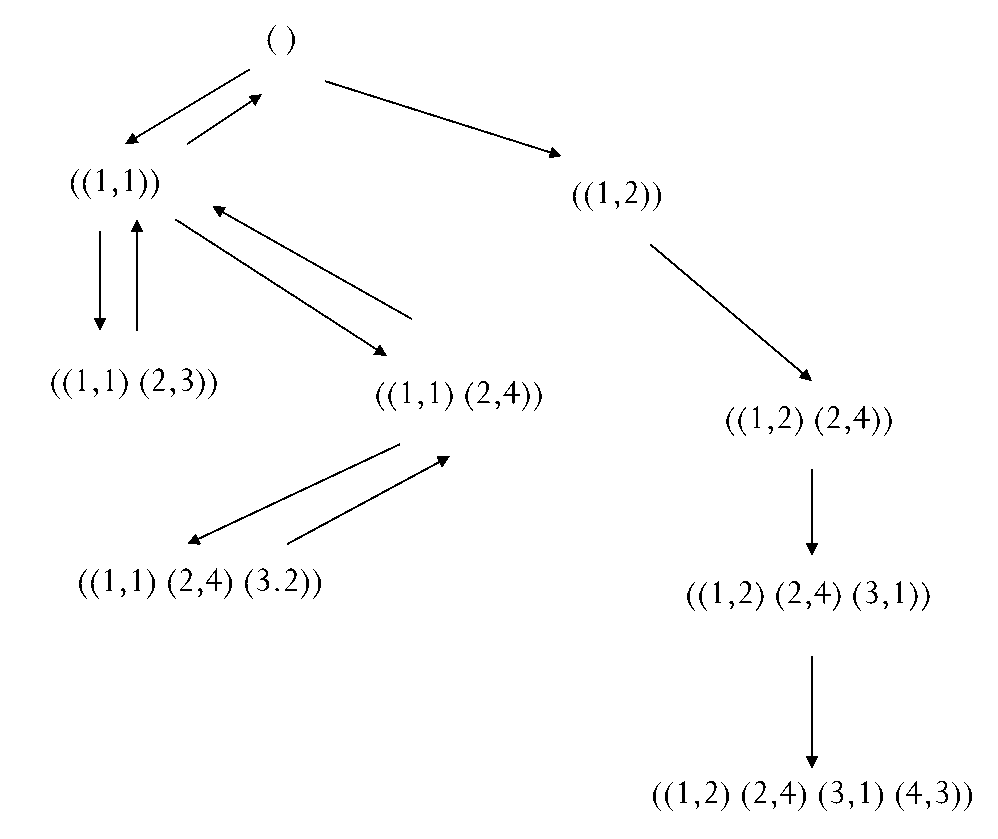
图3.26 四皇后问题搜索图
图3.26给出了采用深度优先搜索算法求解四皇后问题的搜索图。在求解过程中,我们从第一行开始,一行一行地进行由上到下探索。而在每一行,我们从第一列开始,一列一列地从左到右进行探索。具体过程如下:
图中最开始是一个空表,表示棋盘上没有皇后。然后在(1,1)位置放置一个皇后,得到状态((1,1))。
然后在第二行从左到右按列探索。第二行的一、二列都不能再放置皇后了,所以只能在第三列放置第二个皇后,得到状态((1,1),(2,3))。此时我们得到的皇后摆放情况如图3.27所示。

图3.27 皇后的摆放情况示意图
从图中我们可以看出,此时第三行已经不能再放皇后了。虽然第四行还可以继续放皇后,但是由于在4×4的棋盘上摆放4个皇后,每行必须有一个皇后,所以这时就没有必要试探第四行了,相当于进入了死胡同,需要回溯。
回溯的结果是放弃第二个皇后,将其摆放在二行四列试试,得到状态((1,1),(2,4))。
接下来我们可以在第三行的第二列摆放第三个皇后,得到状态((1,1),(2,4),(3,2))。其皇后的摆放情况如图3.28所示。
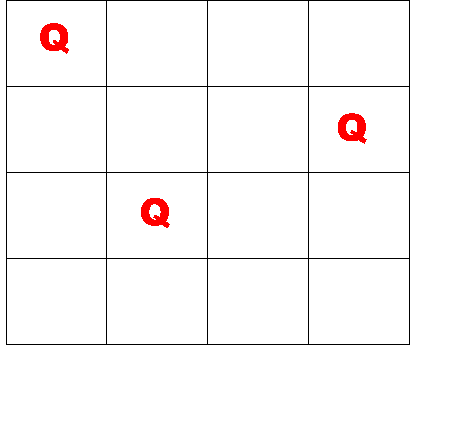
图3.28 皇后的摆放情况示意图
这时我们又发现,第四行也没有任何位置可以放皇后了,说明前面皇后摆放的有问题,再次进入死胡同,需要回溯。
仔细观察图3.28就会发现,第二行、第三行可以摆放皇后的位置都试探过了,不再存在其他的可以摆放皇后的位置,需要连续两次回溯,又回到最初的状态,棋盘上只有(1,1)处有一个皇后。如果在(1,1)有皇后的话,后续就不能按照规则放皇后了,说明(1,1)位置不是一个正确的选择,也需要回溯,这时又变成了一个皇后都没有的空棋盘,似乎又回到了最原始状态。但是与最初的空棋盘不同的是,我们知道了不能在(1,1)位置摆放皇后这一信息。接下来就可以试探在(1,2)这个位置摆放皇后,得到状态((1,2))。
然后在第二行第四列放置皇后,得到状态((1,2),(2,4))。
再在第三行第一列放置皇后,得到状态((1,2),(2,4),(3,1))。
最后在第四行第三列放置皇后,得到状态((1,2),(2,4),(3,1),(4,3))。
至此我们就得到了该四皇后问题的解,图3.26清楚地给出了以上搜索过程的示意图。从图中也可以看出,深度优先搜索算法每次优先选择节点深度最深的节点扩展,当被选择的节点没有新的子节点可以生成时,也就是进入了“死胡同”时,则回溯一步,探讨其他的节点深度最深的节点,一直到找到了到达目标的解路径为止,算法成功结束。或者在探索了所有可能之后,仍然没有找到到达目标节点的路径,算法失败退出。
小明问艾博士:如果节点深度最深的节点有多个时如何选择呢?
艾博士回答说:与宽度优先搜索算法一样,可以随机选择一个或者按照某种约定好的规则选择。在这个例子中,我们实际上是按照从左到右的棋盘位置进行选择的,所以在每一行试探时,总是先从左边开始试探。
小明:深度优先搜索算法只有遇到死胡同时才进行回溯吗?
艾博士:遇到死胡同是必须进行回溯的,但是只是这一种回溯条件,对于很多实际问题可能会有问题。比如我们想在地图上寻找清华大学到达香山的路径,由于道路四通八达,几乎遇不到死胡同,如果按照深度优先算法的原则每次都选择深度最深的节点扩展,则可能会沿着某条高速路一直搜索下去,而很难到达香山。比如沿着八达岭高速走下去,可能就一直到达西藏拉萨了。这显然是不可取的。这种时候,可以设置“深度限制”作为回溯的一个条件。
小明问:如何增加深度限制呢?
艾博士:比如说,我们大概知道从清华大学到达香山的距离大约为15公里左右,不会超过20公里,则可以设置深度限制为20公里,如果从初始节点到被选择扩展的节点距离超过了20公里,虽然不是死胡同,也进行回溯,不再试探下去。
小明:这倒是一个解决办法。
艾博士:深度优先搜索中可能还会遇到“死循环”的问题。还是用搜索从清华大学到香山的路径为例,可能走到了北京四环公路上,四环公路是一个环形公路,进入以后就可能沿着四环转起圈来。一种解决办法就是在搜索过程中,记录从初始节点到目标节点的路径,每次选择一个节点扩展时,判断一下该节点是否在该路径上,如果在该路径上就进行回溯,从而避免了死循环情况的发生。
加深度限制和循环检测是深度优先搜索算法中除了死胡同以外的两个常用回溯点。
接下来艾博士给小明留了一个练习题,用深度优先搜索算法求解如图3.29所示的八数码问题,并假定深度限制为4。
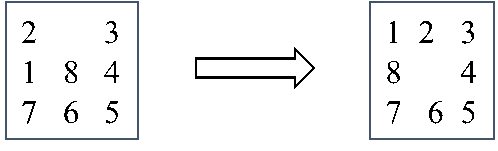
图3.29 八数码问题
小明见艾博士留了练习题,马上认真做了起来,不一会功夫就给出了如图3.30所示的该问题的搜索图。图中用带红圈的数字和英文字母表示节点的扩展次序(1~9以后用a、b、c…表示),每次达到深度限制条件时进行回溯。通过搜索图可以得到该八数码问题的解为:将牌2右移、将牌1上移、将牌8左移。
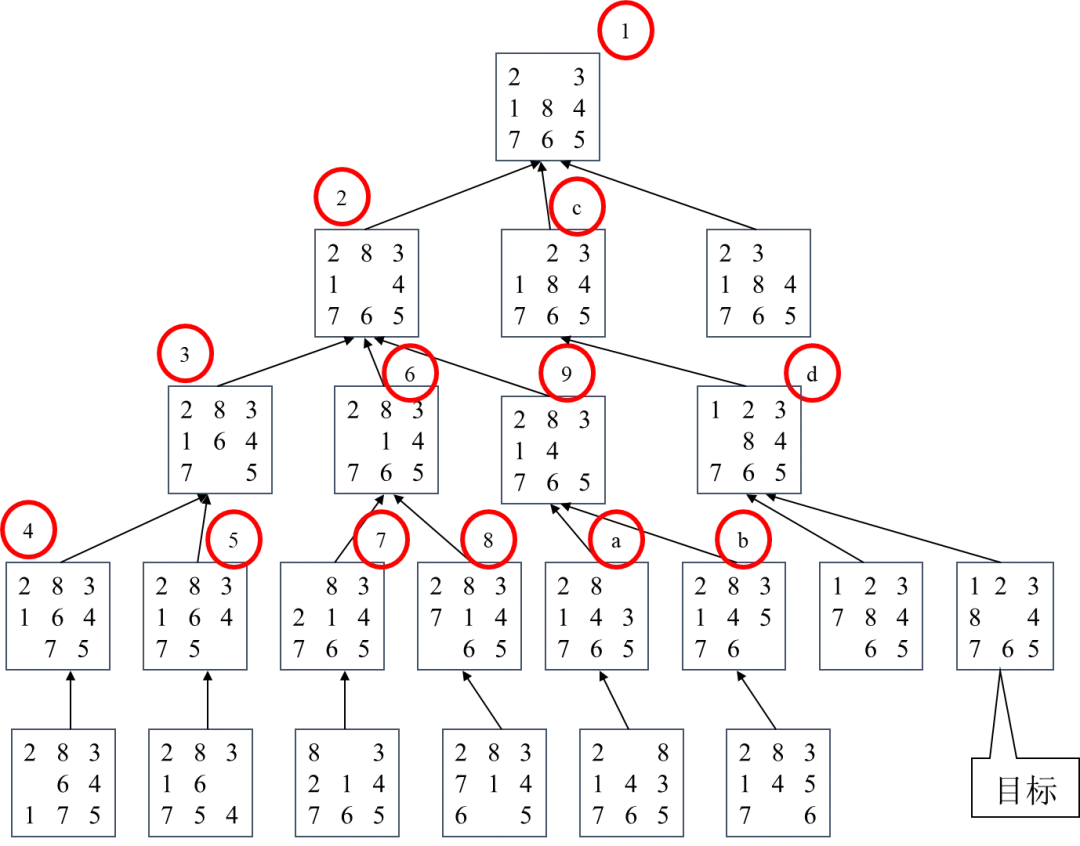
图3.30 深度优先搜索算法求解八数码问题示意图
艾博士:深度优先搜索算法属于盲目搜索算法,最坏的情况下等同于穷举搜索。但有时结合具体问题,也可以在深度优先搜索中引入知识,利用知识减小问题的搜索空间。
小明:深度优先搜索算法还可以引入知识?怎么引入呢?
艾博士:我们通过一个例子说明这个问题。设有1~9九个数字,九个数字的任何一个排列都组成了一个9位数整数。问是否存在一个排列,使得前i个数字组成的i位整数能被i整除。比如327654189是一个九位数整数,前1位数字组成的整数为3,肯定能被1整除,前2位组成的整数为32,也容易验证能被2整除,前3位组成的整数为327,也满足条件能被3整除……,一直验证下去,发现前7位组成的整数3276541是不能被7整除的,前8位组成的整数32765418也不能被8整除,所以这个9位数整数不符合题目要求。那么是否存在某个排列满足题目的要求呢?如果用深度优先搜索算法直接求解的话,9个数字的排列数共有9!=362880个。能否利用知识减少这个问题的搜索空间呢?答案是肯定的,一些简单的知识就可以大幅度减少该问题的搜索空间。
小明:有哪些知识可以利用呢?又如何利用这些知识呢?
艾博士:小明,首先我们看“前5位数组成的整数被5整除”。什么样的数字才能被5整除呢?
小明回答说:最后一位是5或者是0的整数才能被5整除。
艾博士:对,这就是一个可用的知识。在我们这个问题中,不包含数字0,所以如果这个5位数如果能被5整除的话,只有一种情况满足这个条件,就是第5位必须为5。依据这条知识,5这个数字只能也必须排在第5位。
小明:只能是这个结果,否则就不能满足“前5位数组成的整数被5整除”这个条件了。
艾博士:能被2、4、6、8整除的整数,最后一位必须是偶数,所以排在偶数位的数字必须是偶数。共有4个偶数位,偶数也是4个,所以排在偶数位的数字必须是偶数。还剩下1、3、7、9四个数字,这4个数字也就只能排在1、3、7、9这4个位置了。这样一来,2、4、6、8这4个数字有4个位置可放,1、3、7、9这4个数字也有4个位置可放,5只有第5位这一个位置,所以可能的组合共有4!×4!=576个,比起9个数字的排列数9!=362880少太多了,有效减少了搜索空间,提高了搜索的效率。
小明:真是一个令人惊喜的结果,只是简单地利用了这些很基本的知识就起到了这样的效果。
艾博士:因此在具体使用搜索算法时,要尽可能地挖掘待求解问题的一些知识,利用知识提高搜索效率。
小明又问艾博士:深度优先搜索算法有什么优点呢?从搜索过程很难看出有什么优点来。
艾博士:深度优先搜索不能保证找到最优解,甚至在深度限制不合理的情况下,比如深度限制的太小了,甚至都可能找不到解,搜索效率也很低,最坏情况下等同于穷举搜索。从这些看起来似乎深度优先确实没什么可取之处。但是有些问题并不需要找最优解,只要找到解就可以。比如四皇后问题就是这样的问题。深度优先搜索算法最大的优势是比较节省存储空间,因为每当回溯时都可以释放掉用于存储节点的空间,只保留从初始节点到当前节点的一条路径就可以了,所用空间与找到的解的深度成线性关系,所以占用空间比较少。而宽度优先搜索算法需要将所有产生的节点全部保留起来,随着搜索的进行,所需要的存储空间是呈指数增长的,指数增长是非常可怕的增长,非常消耗存储空间,对于稍微复杂一点问题,就可能由于空间被消耗掉而不能求解。即便是A*算法,多数情况下其占用的空间也是指数增长的,当求解比较复杂问题时空间消耗非常严重。
小明:艾博士,我明白了,深度优先搜索算法最大的优势就是比较节省空间,所用空间与解的深度呈线性关系。
小明读书笔记
深度优先搜索算法每次选择节点深度最深的节点扩展,由于存在可能的“深渊”或者“死循环”,一般会加上深度限制和循环检测。深度优先搜索不能保证找到最优解,如果深度限制不当,还可能找不到解,即便问题是有解的。深度优先搜索的优势是占用空间比较少,因为每次回溯时,都可以将相关节点释放掉,只保留从初始节点到当前节点的路径即可。
在深度优先搜索算法中也可以利用知识减少搜索范围,根据待求解问题的特点,适当地引入知识,可以有效提高算法的搜索效率。
未完待续

