第三篇 计算机是如何找到最优路径的(六)
清华大学计算机系 马少平
第六节:迭代加深式搜索算法
小明:深度优先搜索算法虽然比较节省内存,但是不能保证找到最优解,能找到最优解的宽度优先搜索算法、A*算法等占用空间又比较大,如果需要找到最优解,空间又不够用时怎么办呢?
艾博士:一种解决办法就是将深度优先搜索算法与其他方法相结合,做到既节省空间,又可以找到最优解。
小明不解地问:会有这么两全其美的方法吗?
艾博士:我们将要介绍的迭代加深式搜索算法就属于这类方法,但是是以增加算法的运行时间为代价的。下面我们介绍其中的两个方法,一个是深度优先搜索算法与宽度优先搜索结合得到的迭代加深式宽度优先搜索算法,另一个是深度优先搜索算法与A*算法结合得到的迭代加深式A*算法。这两个算法的特点是利用原有算法的思想,用深度优先搜索算法实现,达到即节省算法占用空间,又可以找到最优解的目的。
1、迭代加深式宽度优先搜索算法
艾博士:宽度优先搜索算法实质上是先扩展深度为1的节点,再扩展深度为2的节点,逐渐加深扩展节点的深度。利用这一特性,我们可以用带深度限制的深度优先搜索算法模拟宽度优先搜索。具体说就是,设置一个深度限制d,从d=1开始做深度优先搜索,然后逐渐增加d的值,直到找到目标节点为止。
小明:是不是d=1做一次深度优先搜索,d=2做一次深度优先搜索……一直做下去,直到找到了目标节点为止?
艾博士:是这样的。这与宽度优先搜索算法的效果是完全一样的,找到的解也是一样的,在单位代价条件下宽度优先搜索算法可以找到最优解,那么这种迭代加深式宽度优先搜索算法也同样可以找到最优解结束。
小明:但是由于深度优先搜索算法每次只保留从初始节点到当前节点的一条路径,也正是因为这样,才使得深度优先搜索算法比较节省空间。但是在迭代加深式搜索中,当每次深度限制被改变时,岂不是每次都需要从头开始做一次深度优先搜索?这样搜索速度是不是就太慢了?
艾博士:确实影响了搜索速度。这种方法一般是在由于存储空间不够用的情况下才采用的方法,速度慢一些总比因空间不够无法求解要好,对不对?
小明:这一点确实是这样的,能求出解总比求不出来强得多。
艾博士:事实上,迭代加深式宽度优先搜索算法相比原始的宽度优先搜索算法也不是想象的那么慢,其速度还是可以接受的。下面我们就分析一下,看看迭代加深式搜索算法会慢到什么程度。
为了分析上的方便,我们假设在一个满b叉树上进行搜索,目标节点的深度为d。有理由认为算法所需要的时间与所产生的节点数成正比,这样,我们只需分析两个算法所产生的节点数的关系即可。
讲到这里艾博士问到:小明,你知道如何计算一个深度为d的满b叉树的节点数吗?
小明思考了一下回答说:设宽度优先搜索算法产生的节点数记为NBF,则有:
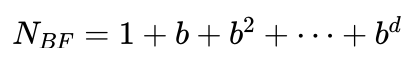
艾博士又接着问:同样是这个深度为d的满b叉树,如果采用迭代加深式宽度优先搜索算法,会产生多少个节点呢?
小明经过思考后说:这个要复杂一些,因为对于迭代加深式宽度优选搜索算法来说,从深度0开始到深度d为止,每个深度下都要搜索一遍,而每一遍搜索都会产生和同样深度下宽度优先搜索算法同样多的节点数。即第i次搜索产生的节点数为:
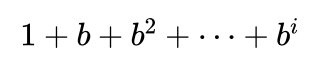
这些节点数再累加起来就是迭代加深式宽度优先搜索算法所产生的节点数。
设迭代加深式宽度优先搜索算法产生的节点数为NIDBF,则有:
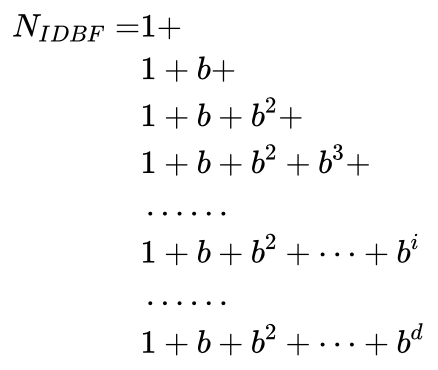
其中第i行对应着第i次搜索所产生的节点数。整理后有:

这个求和并不好直接求解,我们变换一下:
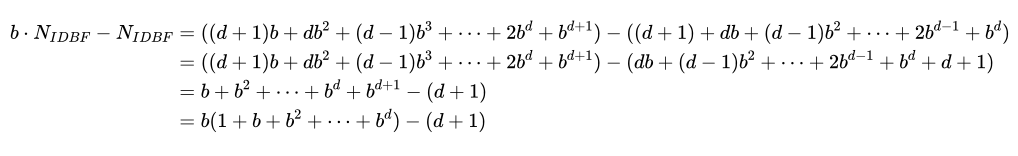
而其中的 (1+b+b^2+...+b^d) 刚好是我们前面计算的宽度优先搜索算法产生的节点数 Nbf ,所以有:
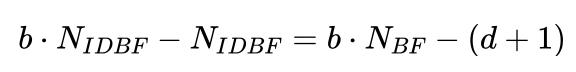
求解有:
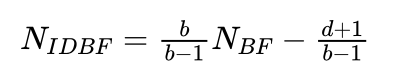
艾博士看着小明的求解结果夸奖到:小明很擅长求和计算么,正是这个结果。
紧接着艾博士分析说:由于分叉数b≥2,所以:
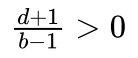
所以有:
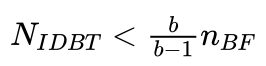
也就是说,在一个满的b叉树上做搜索的话,迭代加深式宽度优先搜索算法产生的节点数小于宽度优先搜索算法产生的节点数的 b/(b-1) 倍。分支数越大,二者所用时间越接近。表3.4给出了不同b值时所用时间比k,当b=2时k值最大为2。也就是说,迭代加深式宽度优先搜索算法所用时间不会超过宽度优先搜索算法所用时间的2倍。当然这是在满的b叉树上做搜索得到的结论,实际情况可能会有些不同,但大体上差不多是这个结论。
表3.4 迭代加深式宽度优先搜索所有时间比

看完艾博士给出的结果,小明有些惊愕:迭代加深式宽度优先搜索算法所用的时间确实比想想的要少,当空间不够用时,确实是一个可采用的方法。
艾博士:迭代加深式搜索算法除了为了节省空间外,还可以应用到一些在规定的时间内,尽可能做出最优选择的场合。比如我们在第二篇介绍的α-β剪枝算法,一般来说搜索的深度越深,其性能越好,但是一般情况下每一步的下棋时间会有所限制,不能超时。这时也可以采用这种迭代加深式搜索,在做α-β剪枝时,并不限制一个固定的深度,而是逐步加深搜索范围,在限时快结束时,用当前得到的最好结果作为决策。否则如果开始设置的搜索深度过深,可能限时结束时还得不到结果。反之如果设置的搜索深度过浅,则没有充分利用时间,没能得到一个更好的下棋决策。
小明:迭代加深式搜索算法还可以这么用啊,还真没有想到。
2、迭代加深式A*算法
艾博士:同迭代加深式宽度优先搜索算算法一样,类似的思想也可以与A*算法相结合,得到迭代加深式A*算法,用比较少的空间,获得和A*算法一样的搜索效果,这样的算法称作IDA*算法。
在迭代加深式宽度优先搜索中,通过限制被扩展节点的深度,并逐渐加深该限制,实现用深度优先搜索算法模拟宽度优先搜索算法的目的。IDA*算法也是类似的思想,只是把深度限制用A*算法中的f函数值代替,在每次做深度优先搜索时,如果被选中扩展的节点的f值大于给定值 f0 时,则进行回溯。如果本次深度优先搜索没有找到目标节点,则加大 f0 值,再次进行深度受限的深度优先搜索。采用这种循环调用深度优先搜索的方法,逐渐加大f0 值,直到找到目标节点为止。
小明:对于迭代加深式宽度优先搜索,每次对深度限制加1就可以了,在IDA*中如何加大 f0 的值呢?
艾博士:一种简单的方法就是记录本次深度优先搜索过程中,因选中扩展的节点f值大于f0 而进行回溯时的节点,选择其中最小的f值,作为下次深度优先搜索时的 f0 值。这样IDA*算法就可以用比较少的搜索空间,而达到和A*算法同样的目的,得到问题的最优解。
小明:看起来迭代加深式搜索算法对于解决空间不足的问题还是很有效的,虽然会增加一些运算时间。
艾博士:迭代加深式搜索算法其中心思想就是用时间换区空间,这是解决空间不足问题时一种常用的解决方法。
小明读书笔记
宽度优先搜索、A*算法具有比较好的性质,但是由于搜索过程中会保留全部生成出的节点,当问题比较复杂时,占用空间比较大,以至于可能因为空间不够而不能求解。
可以将深度优先搜索算法和宽度优先搜索算法、A*算法结合起来,在占用空间比较少的情况下,达到宽度优先搜索算法或者A*算法的搜索性能,找到问题的最优解。其基本思想就是通过逐步加深搜索的方法模拟宽度优先搜索或者A*算法。这类搜索方法称为迭代加深式搜索。
深度优先搜索算法与宽度优先搜索算法结合,是设置一个搜索深度限制d,然后用深度优先搜索算法进行搜索,如果找不到解,就将深度限制加1,逐步加深搜索限制,直到找到解为止。该方法模拟了宽度优先搜索算法一步步加深搜索的过程,所以找到的解和宽度优先搜索算法找到的解是一样的,同样可以在单位代价下找到最优解。
深度优先搜索算法与A*算法结合也采用类似的思想,得到的算法称为IDA*算法。同样设置一个搜索深度限制,只是不用节点的深度作为限制条件,而是将所允许的最大f值 f0 作为限制条件。在进行深度优先搜索过程中,增加一个回溯条件:如果被选择扩展的节点其f值大于 f0 ,则发生回溯。如果找不到解,就加大 f0 值,再次调用深度优先搜索。通过逐步加大 f0 的方法,逐渐扩展搜索范围,直到找到解为止。
如何加大f0 值呢?一种可行的办法是,从因f值大于 f0 而发生回溯的节点中,选择一个最小的f值,作为下次深度优先搜索时的 f0 。
这样就实现了在占用空间比较小的情况下,达到找到最优解的目的。
未完待续

