第四篇 如何用随机算法求解组合优化问题(十)
清华大学计算机系 马少平
第十节:遗传算法的实现问题
艾博士:在前面遗传算法的介绍中我们只是给了一个基本的算法框架,要用遗传算法求解实际问题,还有很多问题需要解决,比如编码问题、参数设置问题等。下面我们就一一讨论这几个问题,给出一些指导性的意见。
1. 编码问题
艾博士:在用遗传算法求解问题时,首先遇到的是编码问题。将问题的解以适合于遗传算法求解的形式进行编码,称为遗传算法的表示。而交叉、变异等操作是与具体的编码形式有关的。因此在对问题进行编码时,要考虑到交叉、变异如何操作问题。
最简单的编码是二进制编码,此外还有整数编码、实数编码、树编码等。采用什么样的编码与具体的问题有关。下面给出几个采用二进制方式进行编码的例子。
例:对于前面例题中区间[0,31]上函数 f(x)=x^2 最大值问题,当x不限于整数时,如何编码?
艾博士问小明:你还记得这个题目是如何编码的吗?
小明回答说:当时的题目要求是x取值为区间[0,31]上的整数,在这个区间上共有32个取值,所以刚好可以用5位二进制数表示,因为5位二进制数从00000到11111刚好可以表示32个不同的数。但是对于一般情况如何编码我就不知道怎么做好了。
艾博士:这其实涉及到编码表示的精度问题。因为遗传算法只能处理离散变量,对于连续变量必须做离散化处理,才有可能用遗传算法求解。比如对于这个例题,如果我们不限制x的取值为整数而是可以是区间[0,31]上的任何实数,就需要先对x取值进行离散化处理再进行编码。由于编码是离散的,必然涉及表示精度问题。比如如果每0.1为一个间隔,则x的取值范围为0.0、0.1、0.2、0.3、…、30.1、30.2、…、30.9、31.0,其表示精度就是0.1。如果每0.5为一个间隔,则x的取值范围为0.0、0.5、1.0、1.5、…、30.0、30.5、31.0,其表示精度为0.5。从求解结果的角度,当然是精度越高越好,但是精度越高的话,所要表达的离散结果就越多,每个个体的编码就越长,从而会影响算法的求解效率和效果。所以应该在满足表示精度的情况下,尽可能采用最短的编码长度。
小明:那么表示精度与编码长度之间具有什么关系呢?
艾博士:我们从更一般的情况考虑这个问题。假定[a,b]为x的取值区间,n为二进制编码长度, ε>0 为所允许的表示误差。则n位二进制数可以表示0到 2^(n-1) 共 2^n 个数。所以n位二进制数可以表示的最大精度为:
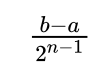
所以只要所选取的n能满足:
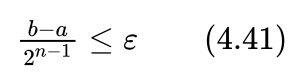
就可以满足精度要求。
比如如果x是区间[0,31]上的整数,则相当于a=0、b=31、精度 =1,所以当n取5时:
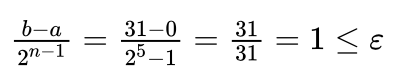
刚好满足精度要求。
由式(4.41)可以得到一般情况下编码长度n为:
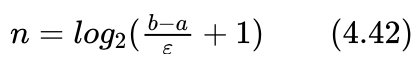
由于编码长度必须为整数,所以当这样计算得到的n含有小数时,就要选取一个大于计算值的最小整数为编码长度。比如还是这个例子,当精度 ε =0.5时,则由式(4.42)求得编码长度:
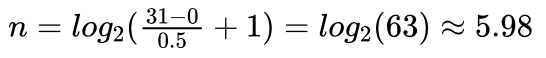
大于计算结果的最小整数为6,所以得到编码长度为6。
小明:可以对计算结果采用“四舍五入”的方法得到编码长度吗?
艾博士:当结果“五入”时没有问题,但是当结果“四舍”时,由于得到的编码长度小于计算结果,可能达不到精度要求。所以必须是只要计算结果含有小数位,就必须“入”到比该结果大的整数。
如果是手工计算的话,一种方便的方法是在取对数前做适当的放大处理,比如:
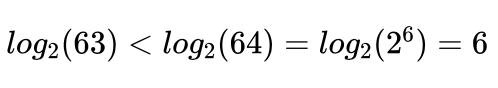
小明:我明白了,这个方法更直接、方便。有了二进制编码长度n,每个二进制编码与x取值如何对应呢?
艾博士:对于在区间[a,b]上的实数x,n位二进制数可以表示0到 2^(n-1) 共 2^n 个数,按从小到大的顺序,第i位编码对应x的第i个取值xi ,则:
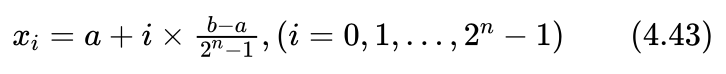
例如对于区间[0,31]上的数值x,当精度 ε=0.5时,计算的编码长度为6,则离散化得x取值分别是:0、0.49、0.98、1.47、…、30.51、31,对应的编码分别是:000000、000001、000010、000011、…、111110、111111。
讲到这里艾博士又强调说:前面我曾经强调过,这里我再强调一次,二进制编码并不是十进制数转换为二进制数,二者不一定相等,只要有一一对应关系即可,这个例子很好地说明了这个问题。这一点也是初学者容易理解错的地方。
小明看着这个结果有些不解地问:我想象的误差0.5应该是离散化的x每个取值都应该在0.5的倍数上,而这个结果显然不是这样的。
艾博士:这与x的取值区间有关。按照式(4.42)计算出的编码长度肯定可以满足精度要求,比如在这个例子中,实际计算出的精度约为0.49,满足0.5的精度要求。如果区间修改为[0,31.5],小明你算算结果会怎么样?
小明认真计算起来:
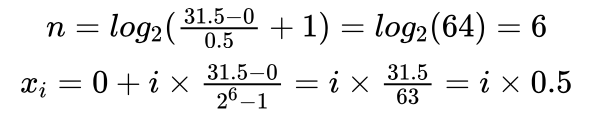
小明:这样修改x的取值区间后,离散化的x取值果然就是0.5的倍数了。但是如果不想改变x的取值区间,是不是可以这样处理:因为以0.5为间隔取值的话,则在[0,31]区间上x共有63个值,而6位二进制数可以表示 2^6=64 个数,我们只用其中的63个编码,比如丢弃111111这个编码,只用000000到111110这63个编码表示x的63个取值,是不是就可以了?
艾博士回答说:这样也是可以的,但是需要解决一个问题。因为在交叉操作或者变异操作中,有可能产生111111这个编码,而该编码又不对应任何x的取值,需要特殊处理一下。
小明用手模着自己的头有点不好意思地说:是有这个问题,我想的简单了。
艾博士:不过这个问题解决起来也不难,只要令111111的适应值等于0就可以了。这样即便在交叉、变异操作中产生了111111这个编码,由于其适应值为0,选择概率也是0,在接下来的选择操作中自然会被淘汰。
小明:这倒是一个很好的解决办法。
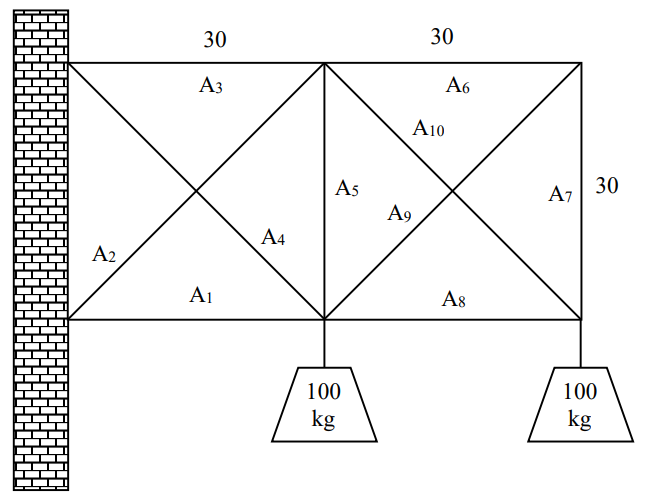
图4.20 十杆桁架问题
艾博士:下面我们再举一个“十杆桁架问题”的例子,该例子选自刘勇等的著作。
例:十杆桁架问题如图4.20所示,其中有10个截面积分别为 A1、A2、...、A10 的杆组成。该桁架由左边的墙支撑,并且它必须承受如图所示的两个负载。每个杆上的应力必须控制在一个允许的范围内,该范围由该杆的应力以某种约束形式表示。问题是如何设计每个杆的截面使得建造该桁架的材料总费用最小。
艾博士:我们在这里只讨论编码问题,不涉及杆的应力是否满足约束问题。假设每个杆的截面积在0.1至10.0之间,在该范围内有16个可能的取值。这样我们可以用4位二进制编码表示截面积的可能取值,其中0000表示0.1,1111表示10.0,余下的14位二进制编码表示其他的截面积的可能取值。这样的话,一个杆需要的截面积就可以用4位二进制表示,共有10个杆,从左到右顺序排列起来,用40位二进制编码就可以表示该十杆桁架问题了。例如,该问题的一个染色体为:
0010 1110 0001 0011 1011 0011 1111 0011 0011 1010
从左到右每4位二进制表示一个杆的截面积。
小明:竟然还可以这样编码,将多个杆的编码组合成一个编码。
艾博士解释说:由于遗传算法不能处理多因素问题,如果涉及多个因素时,就要通过这种办法组合成一个编码。这样才可能用遗传算法求解。
艾博士继续讲解到:小明,看起来二进制编码是不是很简单?但是有时候也会遇到问题。
小明:会遇到哪些问题呢?
艾博士:下面我们以旅行商问题为例说一下可能会遇到的问题,以及解决方案。
对于n个城市的旅行商问题,可以用一个矩阵来表示一个可能解。比如对于4城市的旅行商问题,如下的矩阵可以表示一个可能解。
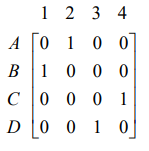
其中行表示不同的城市,列表示城市的访问顺序。第i行第j列如果为1的话,则表示第j个访问的城市是城市i。并默认最后一个城市之后回到第一个城市。由于旅行商问题要求每个城市都必须去1次,而且只能去1次,所以这个矩阵的每一行、每一列必须有一个1,而且也只能有一个1。这是由旅行商问题的约束条件决定的。上例中由于第1列第2行为1,所以出发城市为城市B;第2列第1行为1,说明第2个访问的城市为A,以此类推,我们可以得到该矩阵所表达的旅行商旅行路线是B-A-D-C-B。如果按行展开该矩阵,则该可能解可以用一个长度为4×4的二进制编码表示为:0100100000010010。所以对于一个n城市的旅行商问题,可以用n×n位二进制编码表示一个可能的旅行路线,也就是解。
一个n×n位二进制编码,所有可能的编码个数为 2^n*n ,而一个n城市旅行商问题的可能解个数为n!个。当n比较大时虽然n!是个很大的数,但是比起 来又是小巫见大巫了,只占编码总个数非常小的比例。以n=10为例,编码个数为可能解个数的3.49×1023倍。可见可能解在整个状态空间中是非常稀疏的,交叉或变异操作所产生的结果可能是大量的非可能解,也就是不满足旅行商约束条件的编码。比如某行或者某列多于一个1,或者没有1等。可以想象,对于旅行商问题来说,这样的编码方式,将导致求解效率非常低下,大量时间会花费在非可能解的处理上。所以说对于旅行商问题来说,这样的二进制编码就不是一种可以采用的编码。
小明:那么这个问题怎么解决呢?
艾博士:对于n城市旅行商问题,一种很自然的想法是,对城市进行编号,每个城市分别用1到n之间不同的整数表示,n个整数的一个排列就代表了旅行商问题的一个可能解。这就是所谓的整数编码问题。
小明:整数编码?您快给介绍介绍。
艾博士:整数编码其实并不复杂,对于n城市旅行商问题,从1到n给每个城市唯一的整数编号,这组整数任意一个排列就代表了旅行商问题的一个可能解,其整数编号的顺序就代表了一条可能的旅行路径。比如对于含有A、B、C、D、E等5个城市的旅行商问题,分别用1、2、3、4、5作为城市A、B、C、D、E的编号,则旅行路径B-A-D-C-E-B的编码可以表示为21435。由于这个编码中每个城市的编号都出现了一次,并且只出现了一次,所以是一个满足旅行商问题约束条件的解。
小明:这种整数编码只适用于求解旅行商问题吗?
艾博士:不是的,比如对于皇后问题也可以采用整数编码。小明还记得什么是皇后问题吧?
小明:我记得呢。皇后问题就是在大小为n×n的棋盘上,摆放n个皇后,使得每行、每列和任何对角线上最多只能有一个皇后。
艾博士:对皇后问题也可以采用整数编码,用从1到n共n个整数的排列表示一个可能的解,其中整数值表示皇后所在的列,整数所在的位置,即排列的第几个数,表示皇后所在的行。比如对于四皇后问题,2413表示第一行第二列、第二行第四列、第三行第一列和第四行第三列位置各有一个皇后。
小明:我想起来了,前面您讲局部搜索算法时,曾经采用过这种表示方法。
小明接着问到:对于整数编码如何进行交叉操作和变异操作呢?
艾博士:在这里我们先只讲编码,其他问题我们将会在后面结合相关内容再做具体讲解。
艾博士接着介绍说:除了二进制编码、整数编码外,还有一些其他的编码方法,比如实数编码、树编码等,这些我们就不做介绍了,有兴趣的话可以参阅有关书籍。
小明:好的,课后我去图书馆找找相关内容的书籍。
2. 二进制编码的交叉操作规则
艾博士:在遗传算法中通过交叉操作达到繁衍后代的目的。交叉操作规则与具体的编码方式有关,下面我们首先介绍几种二进制编码中常用的交叉操作规则。
(1)双亲双子法
艾博士:双亲双子法就是前面我们已经介绍过的最常用的交叉方法。当参与交叉的两个双亲染色体确定后,随机地产生一个交叉位,双亲染色体交换各自的交叉位之后的基因给对方,得到两个后代染色体。其交叉操作示意图如下图所示。
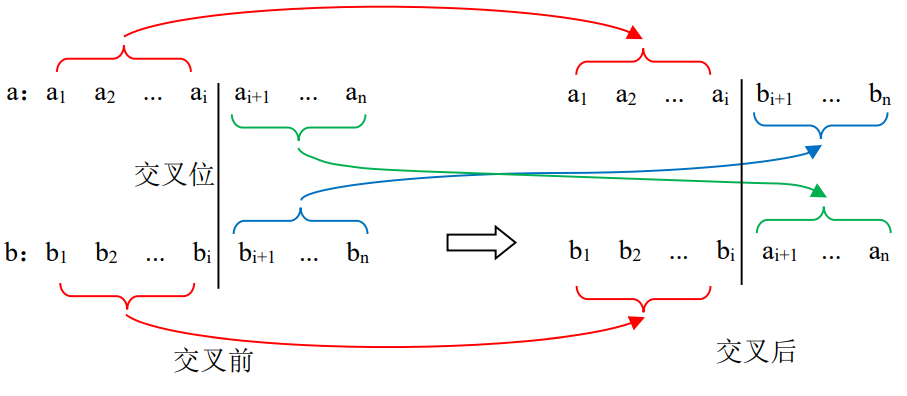
图4.21 双亲双子法交叉示意图
(2)变化交叉法
艾博士:该方法是对双亲双子法的一种改进。交叉操作的目的就是产生具有双亲基因又与双亲有差别的后代。但是在有些特殊情况下,采用双亲双子法交叉得到的两个子染色体可能与其双亲完全一样,这样就失去了交叉操作的意义。比如下面所示的两个染色体:
1 1 0 1 0 0 1
1 1 0 0 0 1 0
由于两个双亲染色体的前三位完全一样,因此当交叉位出现在前三位时,其后代染色体将与两个双亲染色体完全一样。
变化交叉法就是在随机产生交叉位时,排除掉这样的可能结果,产生与双亲不一样的后代。
小明:也就是说,当发现后代与双亲一样时,再重新选择交叉位,以便产生与双亲不一样的后代。
艾博士:对,就是这样的。
(3)多交叉位法
艾博士:前面讲的双亲双子法只有一个交叉位,也可以随机产生多个交叉位,在交叉操作时采用交叉区间交替进行的方法。对于长度为n的染色体,设随机产生了m个交叉位,m个交叉位将双亲染色体划分成m+1段。在交叉操作时,从双亲1取奇数段,从双亲2取偶数段,按顺序拼接在一起作为后代1的染色体。然后再从双亲2取奇数段,从双亲1取偶数段,按顺序拼接在一起作为后代2的染色体。
比如下例中给出的是3个交叉位的情况,三个交叉位分别处于2、4、6位置,得到的两个后代如图4.22右边所示。
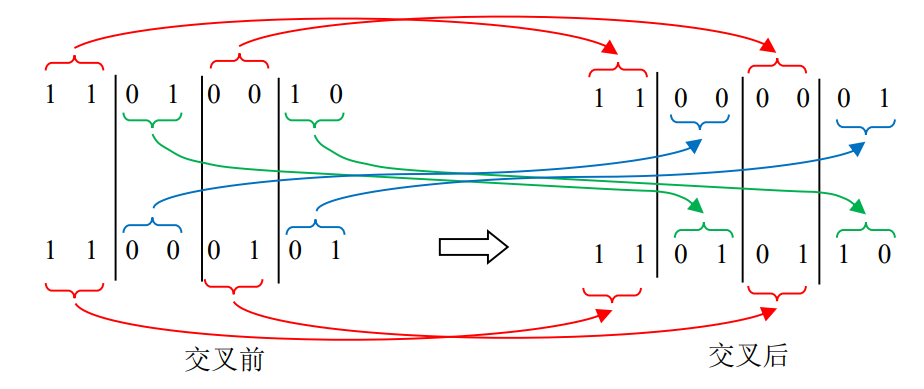
图4.22 多交叉位法交叉示意图
小明:多交叉位法是一种更通用的方法吧?双亲双子法应该是只有一个交叉位时的特例。
艾博士:确实如小明所说,多交叉位法包含了双亲双子法。
小明:如何确定具有几个交叉位呢?
艾博士:具体有几个交叉位也可以随机产生,并不要求每次交叉操作时是一样的。
(4)双亲单子法
艾博士:双亲单子法顾名思义就是每次交叉只产生一个后代。一般是从一般的交叉法得到的两个后代染色体中,随机的选择一个,或者选择适应值大的那一个子染色体作为后代,淘汰没有选中的另一个后代。
小明:这样的话就会减少新产生的种群中个体的数量,需要补充吗?
艾博士:这里有很多种处理办法,比如从双亲中再随机选择一个加入到新的种群中,或者将两个双亲和一个后代都加入到新种群中,做选择操作时从新种群中选择指定规模的个体作为新的群体。
3. 整数编码的交叉操作规则
小明:前面您介绍了旅行商问题可以采用整数编码,那么整数编码情况下如何做交叉操作呢?
艾博士:整数编码情况下如果采用类似二进制编码中双亲双子法那样的交叉操作,在有些情况下也许是可行的,但是对于旅行商问题,产生的后代染色体不一定刚好满足“每个城市必须去一次且只能去一次”的约束条件,从而产生无效解。
例如下面这个例子,采用类似于双亲双子法的交叉操作,将双亲1交叉位前的基因与双亲2交叉位后的基因拼接在一起得到后代1:

这样交叉产生的后代1为12343846,城市3和城市4分别被访问了两次,而城市5和城市7则一次也没有访问。所以这样产生的后代是一个无效解。后代2也有类似的问题。
小明:看来整数编码也有问题啊。
艾博士:我们可以针对以整数编码表示的旅行商问题设计一些交叉操作的规则,使其繁衍的后代满足旅行商问题的约束条件。下面就以旅行商问题为例,介绍几种整数编码的交叉操作规则。
(1)常规交叉法
艾博士:该方法与二进制编码中的双亲双子法有些类似,是为了满足旅行商问题的约束条件而设计的一种整数编码条件下的交叉操作方法。设有双亲1和双亲2,交叉后产生后代1和后代2。随机选取一个交叉位,后代1交叉位之前的基因选自双亲1交叉位之前的基因,这一点与二进制编码中的双亲双子法是一样的。但是交叉位之后的基因选取与双亲双子法就不太一样了,而是从双亲2中从左到右按顺序选取那些在后代1中还没有出现过的基因。例如下面的例子:

图4.23 常规交叉法示意图
在这个例子中,后代1交叉位前的4个基因1234选取自双亲1的前4个基因。这样后代1就已经有了1、2、3、4这四个基因,还缺少5、6、7、8这几个基因。然后在双亲2中找到5、6、7、8这几个基因,并按照他们在双亲2中的位置排列,得到5786这个基因次序,将这4个基因按顺序放到后代1的后四个位置,这样就获得了后代1的染色体12345786。对于后代2也同样处理,就可以得到后代2的染色体52173468。这样交叉得到的后代,由于每个用于编码的整数基因都出现了一次,并且只出现了一次,所以是满足旅行商问题的约束条件的。
小明:这种处理方法比较巧妙地解决了整数编码时旅行商的交叉操作问题。
艾博士:常规交叉方法我们还可以给出更一般的形式。在下面的的例子中,假设随机选取的两个交叉位是a和b。当a小于b时,将双亲1中a、b之间的基因直接复制到后代1中,这样后代1中还缺少1、2、7、8四个基因,按照这四个基因在双亲2中的位置,顺序填入到后代1的相应位置中。这样我们就得到了了后代1为27345618。同样的方法我们也可以得到后代2为24731658。
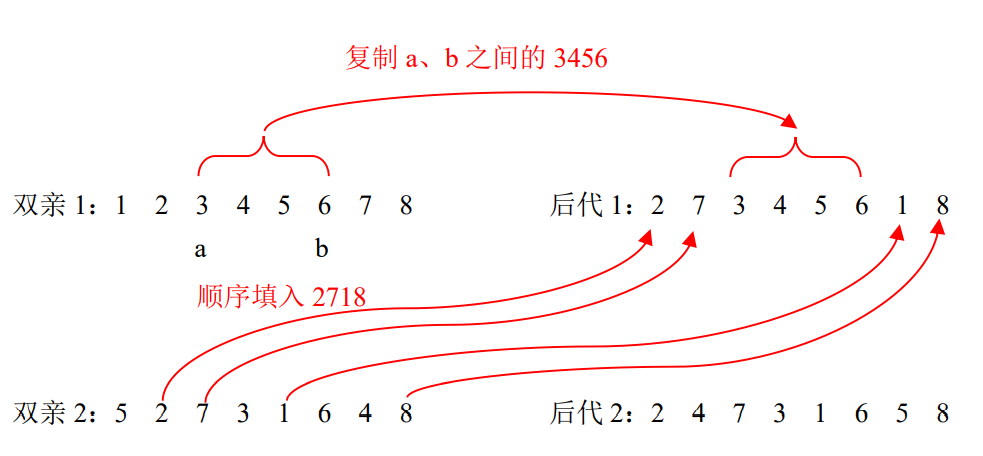
图4.24 一般形式的常规交叉法(a<b时)
如果a大于b时,将编码看成是循环的,则是将b后面到a之前的基因复制到后代1的相应位置中,其他基因按照其在双亲2中的位置顺序补充。这样我们就可以得到后代1为12536478,类似的可以得到后代2为52136748。
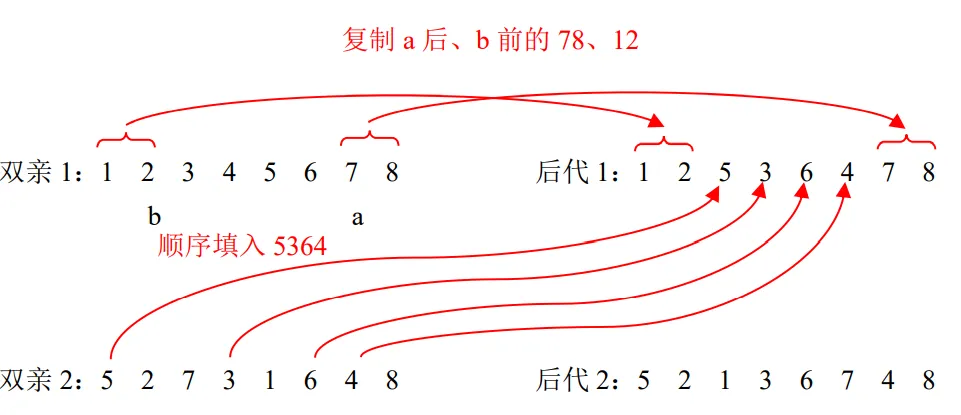
图4.25 一般形式的常规交叉法(a>b时)
小明:这个就更具有一般性了,常规交叉法可以看成是是这种方法当a为1、b为交叉位时的特例。
(2)基于次序的交叉法
艾博士:对于两个选定的双亲1和双亲2,首先随机的选定一组位置,如下例所示,标“*”号的就是选定的位置。
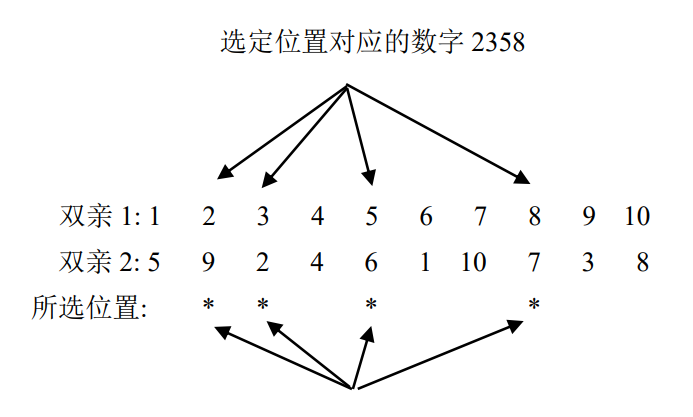
图4.26 随机选定的位置
依次从双亲1中取出与选定位置相对应的数字,在上例中取出的数字为2358,然后在双亲2中找到这几个数字,用表示空位的字母b代替他们的位置。如下图所示。
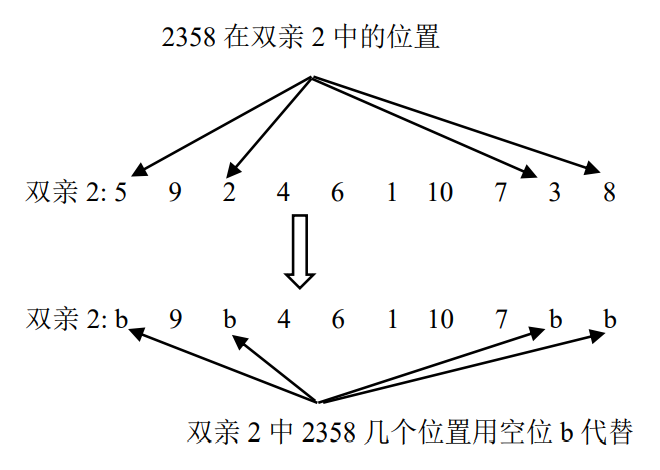
图4.27 空位b示意图
最后按照2358的顺序将这4个数字填入到双亲2的空位中,就得到了后代1。如下图所示。
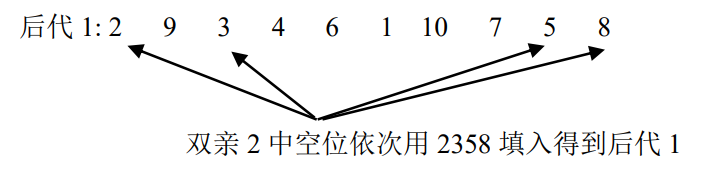
图4.28 填入示意图
这样就得到了后代1为:2 9 3 4 6 1 10 7 5 8。
同样的办法可以得到后代2为:1 9 3 4 5 2 6 8 7 10。
(3)基于位置的交叉法
艾博士:该方法与方法(2)有些类似,对于两个选定的双亲1和双亲2,首先随机产生一组位置。对于这些位置上的基因,后代1从双亲2中直接复制得到,后代1的其他位置的基因,按顺序从双亲1中选取那些不重复的基因。
在下面的例子中,“*”号标注的是随机产生的位置,双亲2在这些位置对应的数字为9263。
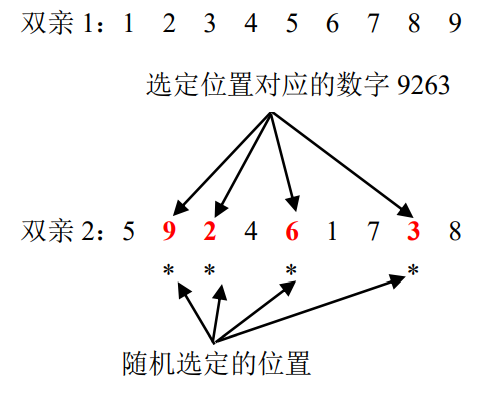
图4.29 随机选定的位置
双亲2中被选中位置的基因为9263,他们分别在双亲2的第2、3、5、8个位置上,因此后代1的第2、3、5、8个位置上的基因依次用9、2、6、3填入。后代1的其他位置上的基因,从父代1中按顺序选取除了9、2、6、3以外的其他基因,按顺序填补到后代1中,如下所示:
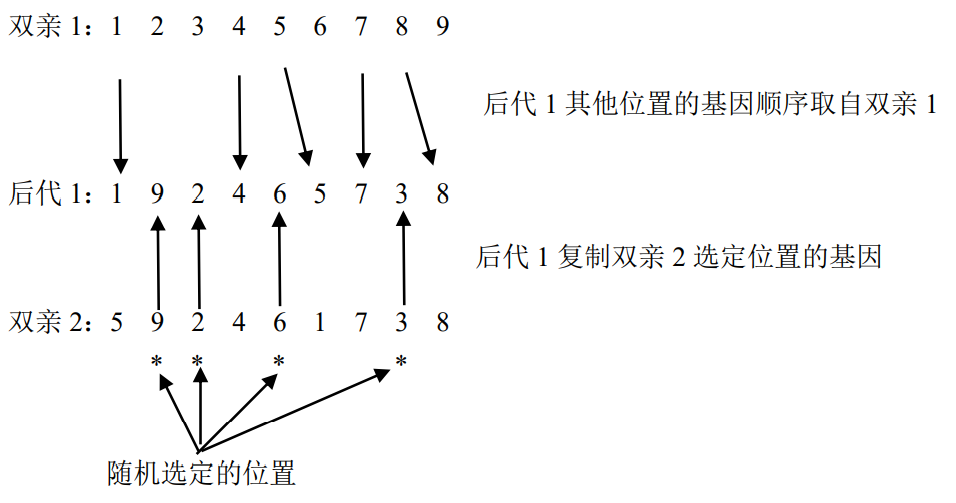
图4.30 基于位置的交叉法
这样就得到了后代1:1 9 2 4 6 5 7 3 8。
依同样的办法也可以得到后代2:9 2 3 4 5 6 1 8 7。
小明:在方法(2)、(3)中,都涉及到了随机产生几个位置的问题,共产生几个位置是如何决定的?
艾博士:位置的数量可以是事先确定的,也可以是随机产生的。
(4)基于部分映射的交叉法
艾博士:对于两个选定的双亲1和双亲2,随机产生两个位置,则两个位置之间的基因按照其位置产生一一对应关系,然后用这种对应关系对分别去替换两个双亲的基因,从而产生两个后代。例如下面给出的例子,其中“*”号表示表示随机产生的两个位置。
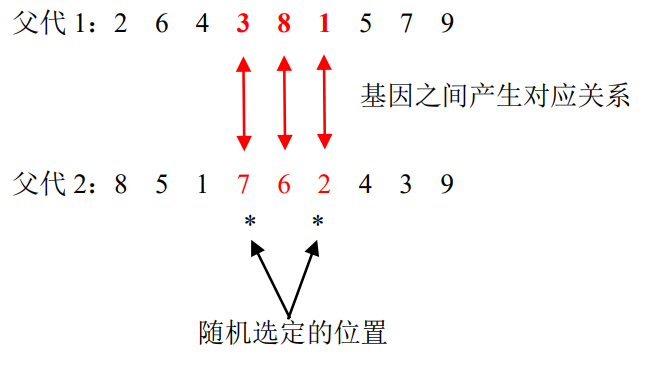
图4.31 一一对应关系示意图
例得到的基因对应对为:3:7、8:6、1:2。然后按照该对应关系分别去替换双亲1和双亲2中的基因,也就是说,原染色体中的基因3用7替换、基因7用3替换,8用6替换、6用8替换,1用2替换、2用1替换。这样就得到了两个后代:
后代1:1 8 4 7 6 2 5 3 9
后代2:6 5 2 3 8 1 4 7 9
艾博士:以上就是一些常用的交叉操作方法,除此之外还有一些其他方法,这里不再一一列举。
4. 变异规则
艾博士:变异是生物进化的重要条件,也是遗传算法以概率1收敛到最优解必须具备的操作。变异发生在某个染色体的某个基因上,它将可变性引入到群体中,增强了群体的多样性,从而提供了一种从早熟中逃脱出来的手段。但是变异虽然可以带来群体的多样性,但因其具有很强的破坏性,因此一般通过一个很小的变异概率来控制它的使用。
在二进制编码情况下,变异方法比较单一,一般是随机地产生一个变异位,被选中的基因如果是“0”则变为“1”,如果是“1”则变为“0”。比如下面这个例子,假定变异发生在染色体的第五位,则对于如下的二进制编码,变异前后的变化如下:
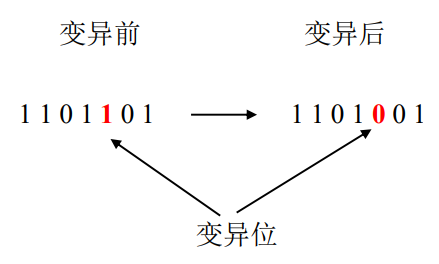
图4.32 二进制编码变异规则
小明:我知道了,这就是我们前面介绍过的方法。
艾博士:在二进制编码中比较容易实现变异,因为只有0或者1两个基因。当问题以整数形式进行编码时,也可以采用类似二进制编码的方法,被选中的基因可以由一个整数随机的变为另一个整数,但这时还必须要考虑染色体的合理性,是否满足约束条件。这时要根据问题本身的性质,合理的定义变异方法。比如对于旅行商问题需要满足该问题的约束条件。下面介绍几种整数编码时的变异方法:。
(1)基于位置的变异
艾博士:该方法随机的产生两个变异位,然后将第二个变异位上的基因移动到第一个变异位之前。例如下面的例子,假定两个变异位分别为2和5,则对于如下的整数编码,变异前后的变化如下:
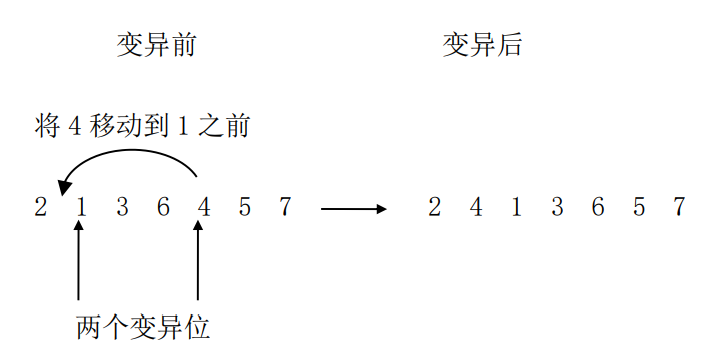
图4.33 基于位置的变异方法
(2)基于次序的变异
艾博士:该方法也是随机地产生两个变异位,然后交换这两个变异位上的基因。例如下面的例子,假定两个随机产生的变异位分别为2和5,则对于如下的整数编码,变异前后的变化如下:
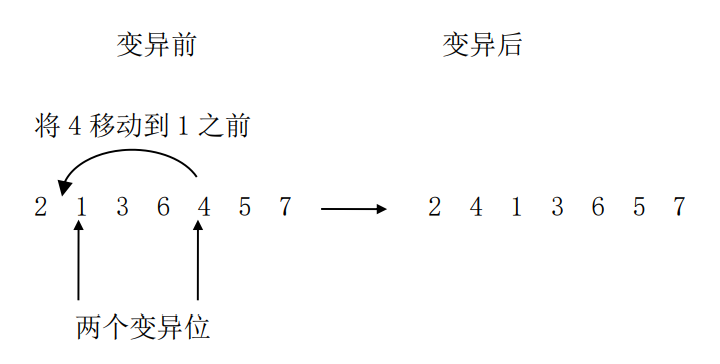
图4.34 基于次序的变异方法
小明:在前面讲解局部搜索时,以旅行商问题为例介绍过邻居的产生方法,其中的“常规交换法”跟这个方法是一样的吧?
艾博士:小明记得很清楚,二者确实是一样的。只是一个用来产生邻居,一个用来进行变异。方法虽然完全一样,但是概念完全不同。
(3)打乱变异
艾博士:打乱变异就是随机选取染色体上的一段基因,然后打乱该段内的基因次序。例如下面的例子,假设随机选取的片段为染色体的第2到第6位,则对于如下的整数编码,其可能的一种变异结果为:
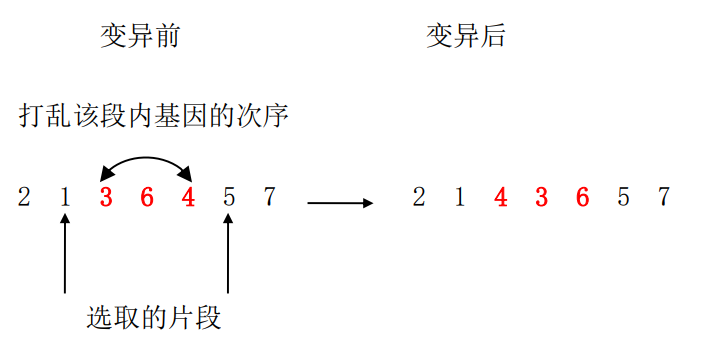
图4.35 打乱变异方法
小明:打乱顺序时没有把处于片段两端的基因“1”和“5”包含在内吗?
艾博士解释说:例子中确实没有包括两端的基因。也可以包括,自己定义清楚就可以了。
讲到这里艾博士问小明:我们前面还讲过旅行商问题产生邻居的另一种方法——“逆序交换法”,小明还记得这个方法吗?
小明:记得呢。我在编写用模拟退火方法求解旅行商问题的程序时,采用的就是这个方法。该方法随机产生两个位置,然后对两个位置之间的城市做逆序交换,就得到了一个邻居。
艾博士:小明说得很清楚,但是你知道逆序交换法跟这里的打乱变异法有什么关系呢?
小明认真思考后恍然大悟到:我知道了,逆序交换法应该是打乱变异法的一个特例,因为如果打乱时采用逆序方法的话,打乱变异法就跟逆序交换法是一样的了。
艾博士:完全正确。我们在学习的时候一定随时了解不同方法之间的区别和联系,这样会更有利于帮助我们学习和掌握学习内容,很多内容都是可以相互借鉴的。
5. 适应函数
艾博士:在遗传算法中,通过将适应函数转化为选择概率,从而实现优胜劣汰的选择策略,所以如何定义适应函数也是采用遗传算法求解实际问题时需要解决的一个重要问题。
一般情况下,我们可以直接选取问题的指标函数作为适应函数。如求函数f(x)的最大值,就可以直接采用f(x)为适应函数。我们前面就有过这样的例子。但是有些情况下也不是直接拿来就可以用的。
小明:什么情况下不能直接将指标函数拿来当作适应函数使用呢?
艾博士:在遗传算法中,适应值必须大于0,因此如果一个函数f(x)<0,就不能直接用f(x)当作适应函数使用。还有,如果希望求f(x)的最小值而不是最大值,也不能直接将f(x)当作适应函数使用,因为遗传算法求的是适应函数的最大值。
小明:确实存在这样的问题,这种情况下应该怎么定义适应函数呢?
艾博士:处理起来也很简单。如果是求最大值,当f(x)<0时,我们可以对f(x)加一个充分大的常数M,使得f(x)+M在x的部分取值下满足f(x)+M>0就可以了。
小明:为什么不要求x在定义域上全部满足f(x)+M>0的要求呢?
艾博士:因为我们用遗传算法求的是f(x)+M的最大值,如果有x的部分取值使得f(x)+M>0,则f(x)+M的最大值一定出现在x的这几个取值处,而不会出现在f(x)+M<0的地方。所以只要x的部分取值使得f(x)+M>0就可以了,没有必要要求在x的全部定义域上满足f(x)+M>0。
小明:但是即便如此,还是可能会出现x的有些取值使得f(x)+M<0,这样的话也不能直接用f(x)+M作为适应函数啊。
艾博士:还需要做一个简单处理,当f(x)+M<0时令其适应函数值为0就可以了。也就是像下面这样定义适应函数:
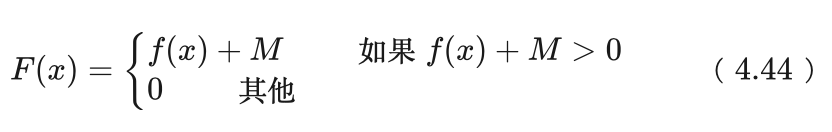
小明:这样就没有问题了,即便有可能存在f(x)+M<0的情况,我们只在f(x)+M>0的范围内求解就可以了。
艾博士:对于求最小值的情况,我们通过增加负号的方法将最小值问题变换为求最大值问题,也就是说求f(x)的最小值和求-f(x)的最大值是等价的。然后再依照上述方法选取一个合适的常数M得到适应函数:
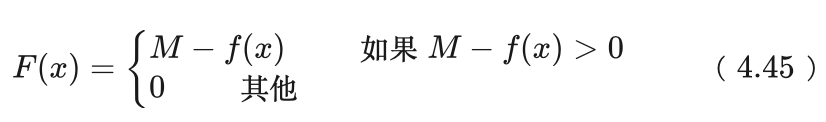
小明:这样一来,前面提到的两个问题就都解决了。
艾博士:定义适应函数还有一些技巧。一般来说,我们希望适应函数不要太平缓,因为太平缓的话,每个个体的选择概率都差不太多,难于体现出优胜劣汰这一进化特性。所以一些研究者提出了一些对适应函数进行“加速”的方法。为了讨论方便,下面我们默认问题的指标函数f(x)>0,并且是求最大值。
小明:什么是加速?如何实现对适应函数加速呢?
艾博士:所谓加速就是加快遗传算法“优胜劣汰”的进程,提高算法的求解效率。其基本思想也比较简单,假设f(x)是问题的指标函数,如果f(x)在最大值附近变化比较缓慢的话,即便是比较好的解,在选择过程中也不具备竞争优势,从而导致进化过程不明显。一种解决方法就是定义一个与f(x)变化趋势一致,但是在最大值附近比较陡峭、变化比较大的适应函数,从而使得比较好的解具有比较大的适应值,提高好解的竞争优势。图4.36给出了一个加速的适应函数示意图。
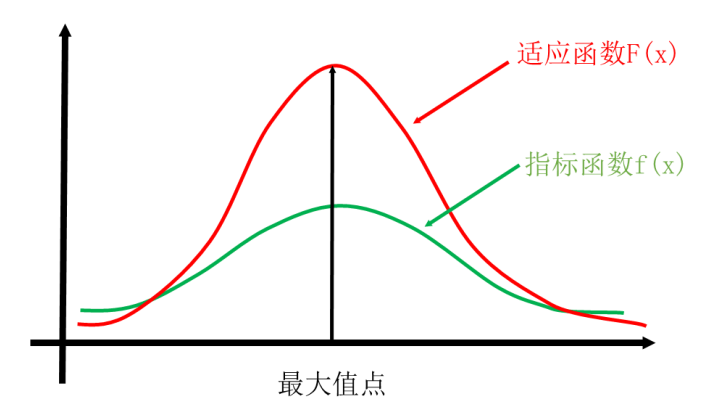
图4.36 适应函数加速示意图
小明:这是一个很好的想法,问题是如何实现这种加速呢?
艾博士:下面介绍几个适应函数加速的方法。
(1)非线性加速适应函数
艾博士:第一种方法是非线性加速适应函数,该方法利用已有的信息构造适应函数:

图4.37给出了该适应函数的示意图。
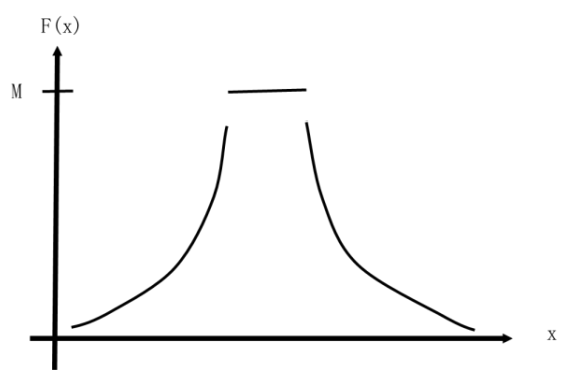
图4.37 非线性加速适应函数示意图
其中f(x)是问题的指标函数,fmax 是当前得到的最大的指标函数值,M是一个充分大的数。M值的大小将影响到算法以怎样的概率选取种群。M不一定是一个常量,可以随着算法的进行而变化,开始时可以相对小一些,以保证种群的多样性,然后可以逐步增大。
(2)线性加速适应函数
艾博士:与非线性加速适应函数相对应的是线性加速适应函数,适应函数与指标函数具有线性关系。其定义如下: 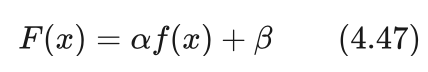
小明:这里的参数α、β如何确定呢?
艾博士:我们可以设立两个原则用于确定线性变换的两个参数α和β,(1)适应函数与指标函数在群体内的平均值相等。(2)群体内最大的适应函数值是群体内指标函数值的M倍,其中M是一个比较大的常数。
小明思考了一下问到:为什么要设立这样的原则呢?出发点是什么?
艾博士解释说:这两条原则,第一条是说适应函数和指标函数的平均值相等,第二条是说适应函数的最大值是指标函数平均值的M倍。在离散的情况下,平均值可以认为是按区间归一化后函数曲线下面的面积。适应函数最大值如果等于指标函数平均值的M倍,而面积又与其相等,则适应函数只能是又“高”又“瘦”的形状。如图4.38所示。
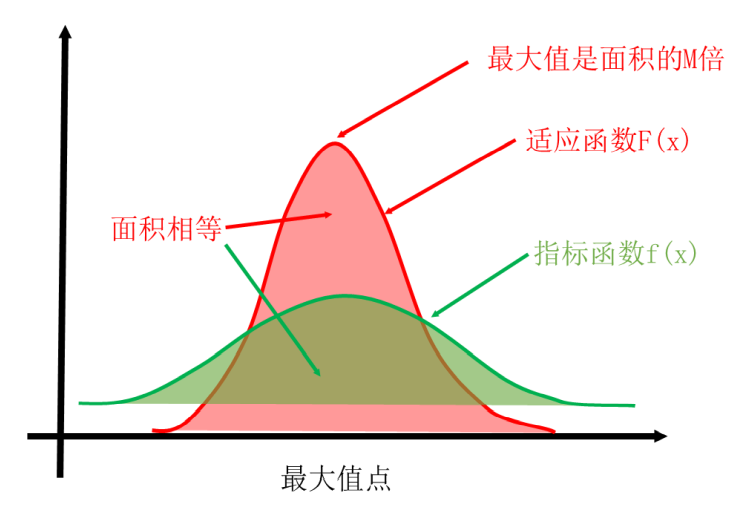
图4.38 线性加速适应函数示意图
小明看着图4.38说:这个图很好地说明了两个原则的含义,由这两个原则就可以确定参数α、β的值吗?
艾博士:可以的。根据这两个原则,我们可以给出一个二元一次方程组,求解这个方程组就可以得到参数α、β的值。
根据第一个原则,适应值和指标函数的平均值相等。假设群体规模为N,xi(i=1,2,...,N) 为群体中的个体。则群体内指标函数的平均值为:
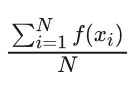
群体内适应函数的平均值为:
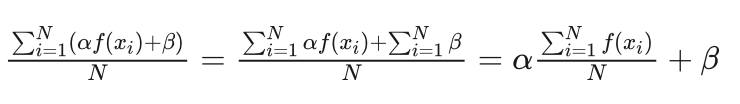
令二者相等我们得到方程组的第一个方程:
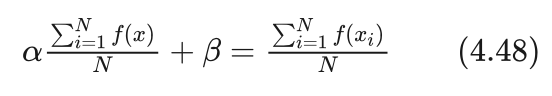
根据第二个原则,群体内适应函数的最大值等于指标函数平均值的M倍。我们先看群体内适应函数的最大值,即:
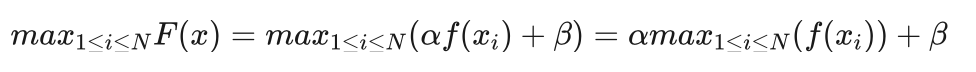
而群体内指标函数平均值的M倍为:
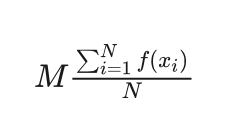
同样令二者相等我们又得到了方程组的第二个方程:
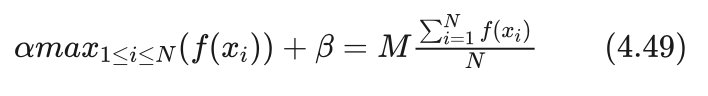
从而我们得到一个一元二次方程组:
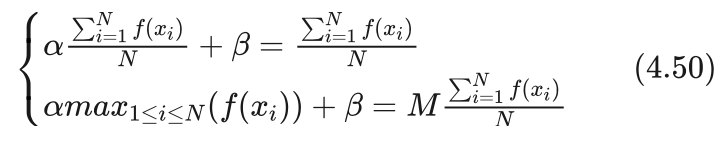
艾博士:小明,二元一次方程组会求解吧?
小明:我们初一就学了,很容易求解。
说着,小明就拿起笔在纸上演算起来,不一会就给出了答案。
小明将答案展示给艾博士:您看,这是我求得的结果:
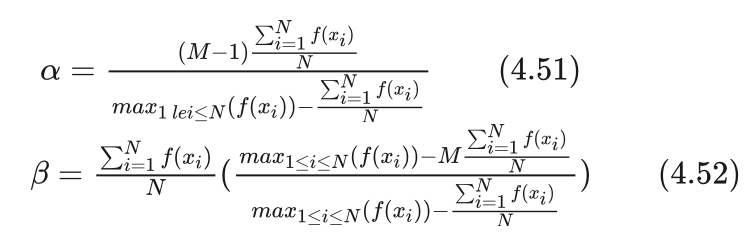
艾博士夸奖小明:你计算的又快又正确,点赞!这个适应函数与每一代的群体有关,不同代中个体的适应值并不是固定的,每次更新新的种群后,都要重新计算一次适应值。
(3)基于排序的适应函数
艾博士:最后我们再介绍一种定义适应函数的方法,该方法先对个体按照其指标函数值从小到大进行排序,然后将个体的排列序号作为其适应函数值。
设群体规模为N,群体内个体按照其指标函数值从小到大排序,其序号分别为1到N。则排序在第i位的个体 xi 被选中的概率为:
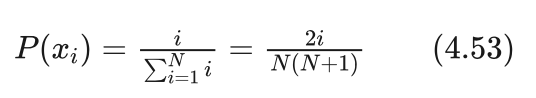
该方法的特点是一个个体被选中的概率与指标函数的区分度无关,只与该个体在群体中的排序位置有关。具有最大指标函数值的个体总是以固定的 2/[N(N-1)] 的概率被选中,而具有最小指标函数值的个体被选中的概率则总是 2/[N(N-1)] 。最大选择概率是最小选择概率的N倍,当群体规模比较大时,也是一个区分性不错的适应函数。
6 遗传算法的停止准则
艾博士:前面我们曾介绍过,当进化代数趋于无穷时,有定理保证遗传算法找到最优解的概率为1。从定理的角度来说,肯定是算法运行的时间越长越好,但显然会存在运行效率问题。在实际计算时,我们希望随时了解遗传算法的进展情况,监视算法的变化趋势,在适当的时候停止算法的运行。常用的方法有如下几种:
(1)当前最好法。
艾博士:该方法在每一代进化过程中,记录到目前为止得到的最好解,通过观察最好解的变化,了解算法的变化趋势。不同的算法之间,也可以通过最好解的变化情况进行横向比较。
(2)在线比较法。
艾博士:该方法用当前代中个体的平均指标函数值来刻划算法的变化趋势。计算方法如下:
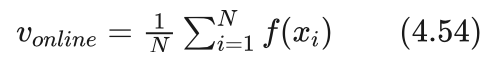
其中N为群体规模,f(xi) 为个体 xi 的指标函数值。
对于最大化问题,遗传算法总是以大概率选择指标函数值大的个体,所以在进化过程中虽然每代的值可能会出现一些波动,但总的趋势应该是上升的,并逐渐趋于稳定。
(3)离线比较法。
艾博士:该方法与在线比较法有些相似,但是用进化过程中每代最好解的指标函数值的平均值来评价算法的进化过程。计算方法如下:
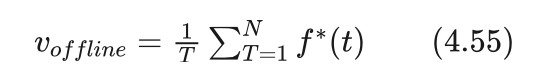
其中T是到目前为止的进化代数,f*(t)是第t代中个体的最好指标函数值。在以最大化为问题的优化目标时,随着算法的进化,该值具有上升的趋势。
艾博士总结说:以上每一种方法,都可以监控算法的进化趋势,掌握遗传算法的进化情进程,从而决定算法是否停止。
小明读书笔记
用遗传算法求解实际问题时,涉及到很多具体的实现问题,这些实现细节对于有效求解实际问题至关重要。包括如何编码、交叉操作、变异操作和适应函数的定义等。
编码方法包括二进制编码、整数编码等,需要根据待求解问题的特点选择合适的编码方式。
交叉操作与具体的编码方法有关,中心问题是如何从两个双亲中选取不同的基因产生两个后代,同时还要考虑产生的后代是否满足问题的约束条件等。
对于二进制编码,交叉操作有双亲双子法,该方法随机产生一个交叉位,交叉位将双亲染色体划分为前后两部分,两个双亲前后部分的不同组合拼接构成了两个后代的染色体。多位交叉法是该方法的推广,每次随机产生多个交叉位,将双亲染色体划分为多个片段,从一个双亲中选择奇数片段,另一个双亲中选择偶数片段,拼接在一起后就构成了两个后代。
对于整数编码,交叉操作有常规交叉法,该方法随即产生一个交叉位,交叉位将双亲染色体划分为前后两部分,双亲1交叉位之前的片段组成后代1的前半部分,从双亲2中按顺序选择那些后代1中还没有出现的基因填充到后代1的后半部分,从而构成了后代1的染色体。类似的方法又可以产生后代2。此外还有基于次序的交叉法、基于位置的交叉法,其基本思想是从一个双亲中选取部分基因到后代中,再从另一个双亲中补充后代中还没有的基因,构成一个后代的染色体。类似的方法再构成另一个后代。基于部分映射的交叉法则是随机产生两个位置,两个位置之间的对应基因构成对应关系,按照对应关系对双亲基因做替换得到两个后代。
变异操作按照概率令某个基因发生突变,对于二进制编码来说,被选中的基因由0变成1或者由1变成0,取决于变异时该基因的取值。对于整数编码来说,有基于位置的变异,该方法随机选择两个基因,将第二个基因放置到第一个基因之前。基于次序的变异方法则是调换两个基因的位置。而打乱变异则是随意打乱两个随机产生的位置之间的基因顺序,逆序交换法是该方法的一个特例。
选取合适的适应函数对于遗传算法有效求解实际问题起着重要作用。为了提高遗传过程中优胜劣汰的效率,提出了非线性加速和线性加速两种适应函数构造方法。其基本思想都是通过让适应函数变得更加陡峭,提高不同个体间选择概率的区分度。
一般通过观察一些变量的变化情况判断遗传算法是否可以停止了。常用的观察方法包括当前最好法、在线比较法和离线比较法等。
未完待续

