第五篇 统计学习方法是如何实现分类与聚类的(五)
清华大学计算机系 马少平
第五节:过拟合问题与剪枝
艾博士:过拟合是机器学习中经常遇到的问题,决策树学习也会遇到过拟合问题。
小明:在第一篇神经网络与深度学习中您曾经介绍过过拟合问题,那么决策树学习中的过拟合问题与之前介绍过的过拟合问题有什么不同呢?
艾博士:从本质上来说并没有什么不同,都是由于样本代表性不强造成的。比如我们举一个生活中的例子。一对双胞胎,我们很难认出哪个是哥哥、哪个是弟弟,如果刚好哥哥有颗痣而弟弟没有,则当遇到这一对双胞胎时,可以通过是否有痣区分哥哥和弟弟。但是这显然不具有代表性,只适用于这一对双胞胎,换成其他的双胞胎就完全无效了。如果把这种特殊情况学习成一般规律,就属于过拟合了。
小明:过拟合会带来哪些不好的影响呢?
艾博士:最主要的影响就是导致学习到的决策树泛化能力差。图5.14给出了一个过拟合问题的示意图。
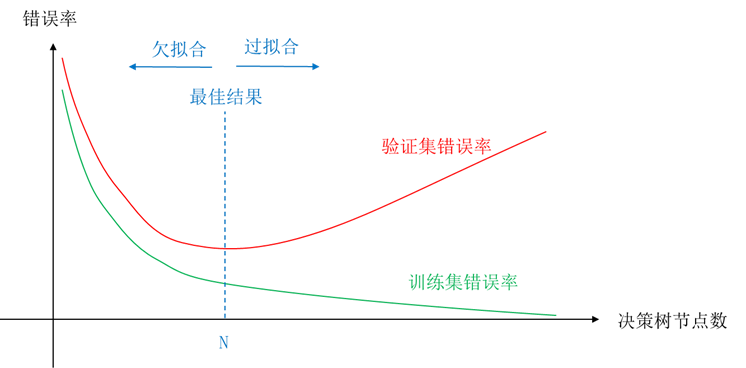
图5.14 过拟合问题示意图
假设我们有两个没有重叠的数据集,一个作为训练集用于训练决策树,一个作为验证集用于测试决策树在不同阶段的性能。在建立决策树的过程中,每增加一个新的节点,就分别用训练集和验证集测试一次决策树的性能,图5.14给出了决策树性能变化的示意图。
图中绿色曲线为在训练集上的错误率曲线,在决策树建立的开始阶段,节点数还比较少,错误率比较高。随着决策树的建立,节点数逐步增多,训练集上的错误率也逐渐减少。这一点比较容易理解,因为在建立决策树的过程中,总是选择信息增益或者信息增益率大的特征对数据集做划分,每使用一次特征都会降低原来数据集的熵,而熵反应了数据的混乱程度,熵越小说明数据越趋于规整,反应在训练集上就是错误率越来越小。
图中红色曲线是在验证集上的错误率曲线,在决策树建立的开始阶段,同训练集上的错误率一样,验证集上的错误率也是随着决策树的建立逐步降低的,当决策树的节点个数达到N时,验证集上的错误率达到了最小值。但是随后随着决策树节点的增加,验证集上的错误率反而会逐步加大,这就是我们称之为过拟合的现象。验证集中的数据由于没有参与训练,所以更接近决策树真实使用时的情况,如果不解决过拟合问题,就会造成决策树的性能下降。
小明:有没有办法解决这个问题呢?
艾博士:从图5.14可以看出,当决策树的节点数小于N时,验证集上的错误率比较高,我们称为欠拟合。过拟合或者欠拟合都不是我们希望的结果,我们希望得到一个恰拟合——最佳拟合结果的决策树,也就是处于N这个位置的决策树。
小明:如何做到这一点呢?
艾博士:这就是我们下面要介绍的剪枝方法。所谓剪枝,就是把过大的决策树剪掉一部分“树枝”,以便使其既不过拟合也不欠拟合,刚好达到恰拟合的效果。
决策树剪枝分为预剪枝和后剪枝两大类方法。预剪枝就是在建立决策树的过程中提前停止决策树某些分枝的建立,达到减小决策树的目的。后剪枝是先按照算法建立好决策树,然后再对决策树做剪枝。小明你还记得在ID3算法的第四步,当最大的信息增益小于阈值时是如何处理的吗?
小明想了一会说:当最大的信息增益小于阈值时,认为特征已经不具有分类能力,等同于特征集为空,不再对数据集做划分,该数据集当作决策树的一个叶节点标记其类别。
艾博士:这其实就是一种简单的预剪枝,这种预剪枝是需要的,但是有些简单,还不足以解决过拟合问题。
比较常用的是后剪枝方法,下面我们主要介绍这种方法。我们先举例说明如何做剪枝。
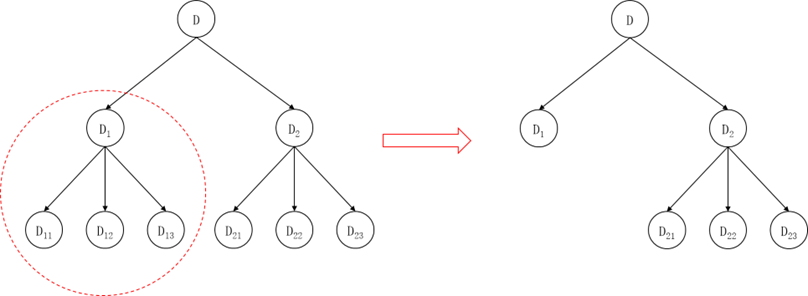
图5.15 剪枝示意图
如图5.15所示,剪枝是从决策树的底部开始进行的,将具有同一个父节点的几个叶节点从决策树中删除,只保留其父节点作为一个叶节点,并将父节点中样本最多的类别作为父节点的类别标记,就完成了一次剪枝。图5.15中左边是剪枝前的决策树,右边是剪枝后的决策树。图中将D11 、D12、D13 三个叶节点剪掉, D1 成为叶节点,按照 D1 中样本最多的类别标注 D1 的类别,同样对 D2 的子节点也可以做一次剪枝。在完成了这两次剪枝后,D1 、D2 都成为了叶节点,还可以进一步再做剪枝,将D1 、D2 剪掉,D也成为了叶节点。这样自底向上可以一步步完成剪枝操作。
小明:那么剪枝到什么时候为止呢?
艾博士:这是一个很好的问题,我们有两种方法可以做出判断。
第一种方法是利用验证集。每做一次剪枝都比较剪枝前后决策树在验证集上的错误率,如果剪枝后错误率下降,则接受这次剪枝,否则就不接受这次剪枝。然后再试探其他可能的剪枝,直到所有可能的剪枝后错误率都不再下降为止。比如图5.15中,如果 D1 的子节点剪掉后错误率下降,则接受这个剪枝,否则就要保留这些子节点,同样如果D2 的子节点剪掉后错误率会下降,则也接受这个剪枝,否则就保留这些子节点。如果D1 、D2 的子节点都被剪掉了,则作为叶节点D1 、D2 也可以被剪掉,至于最终是否被剪掉则取决于剪掉后的错误率变大还是变小。如果 D1 或者D2 中有一个节点的子节点被保留了,那么D1 、D2 这两个节点也就不能被剪掉了。
小明:可能被剪掉的节点一定是叶节点,且一定是一个父节点的所有子节点同时被剪掉或者同时保留,而不能是只剪掉一个节点的部分子节点。
艾博士:小明总结得很好。因为所有子节点被剪掉后,其父节点才可能成为叶节点。剪枝操作一定是几个作为子节点的叶节点同时被剪掉,使其父节点成为叶节点,因为只能对叶节点才有进行类别标注。
小明:明白了,利用验证集的剪枝方法就是通过验证集上的错误率测试剪枝的合理性,自底向上试探每一种可能的剪枝方案,只要错误率下降就认为是合理的、接受该剪枝,直到所有的剪枝方案都不能使得错误率下降为止。
艾博士:下面我们再介绍剪枝的第二种方法。
利用验证集的剪枝方法其优点是简单、可靠,前提是验证集具有足够多的样本。一般来说,在实际问题中收据足够多的数据并不是一件容易的事情,何况在训练决策树时也需要足够多的样本,才有可能得到一个比较好的决策树。有限多的样本要尽可能用在训练上。为此提出了基于损失函数的剪枝方法。
小明:基于损失函数的剪枝方法就不需要验证集了吗?
艾博士:基于损失函数的方法就是充分利用训练集,通过定义损失函数实现剪枝。其想法与利用验证集的剪枝方法基本相同,也是对建立好的决策树自底向上做剪枝,只是在判断剪枝是否合理时,用损失函数代替验证集上的错误率。
小明:我大概了解了基于损失函数的剪枝方法是如何操作的,关键看如何定义损失函数,在只能利用训练集的情况下,如何评价是否过拟合问题。
艾博士:小明你说的很有道理,这里的关键是如何定义损失函数。不同的损失函数定义方法,就产生了不同的剪枝方法。下面我们以其中的一种方法为例介绍如何利用损失函数做剪枝。
在考虑是否过拟合问题时,我们需要从两个方面考虑问题。一是当决策树比较大时,虽然在训练集上的错误率比较低,但是可能产生过拟合问题,剪枝的目的就是减小决策树的规模。二是当决策树比较小时,即便在训练集上也会产生过大的错误率,从而导致欠拟合。所以解决过拟合问题的关键是在决策树的大小与错误率之间做一个折中选择,找到一个合适的平衡点。
如何评价决策树的大小呢?决策树的叶节点个数可以作为评价决策树大小的一个指标,叶节点越多,说明决策树越大、越复杂,叶节点越少,说明决策树越小、越简单。如何反应决策树在训练集上的错误率呢?我们说过,熵的大小代表了数据的混乱程度,一个叶节点的熵如果比较小,就说明这个节点的错误率比较小,所以叶节点的熵是与错误率相关的,我们可以用叶节点的熵表示错误率。但是对于具有相同熵的两个叶节点,其包含的样本数如果不同,对错误率的贡献也是不同的,显然包含的样本越多的节点对于错误率的贡献也越大。这样我们应该对叶节点的熵按照样本的多少做加权处理。
为了表示方便,我们用T表示一个决策树,N(T)表示决策树叶节点的个数,Ti 表示决策树的第i个叶节点,Ni 表示第i个叶节点 Ti 包含的样本数,H(Ti) 表示叶节点 Ti 的熵,α为加权系数。
这样我们可以定义损失函数:
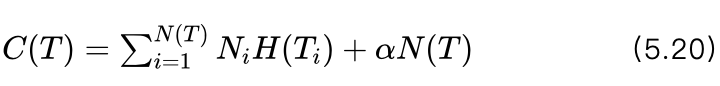
式(5.20)的第一部分是叶节点的熵按照节点所含样本数的加权和,反应的是错误率。第二部分是决策树叶节点的个数,反应的是决策树的复杂程度,加权系数α在两部分之间起到一个调节的作用,较大的α会选择较简单的决策树,而较小的α会选择复杂一些的模型。
基于损失函数的决策树剪枝,就是用损失函数代替验证集上的错误率,用损失函数评价剪枝的合理性,保留那些使得损失函数下降的剪枝,当所有的剪枝都导致损失函数上升时,则停止剪枝。其他方面与使用验证集的剪枝方法是一样的,就不详细叙述了。
小明:基于损失函数的剪枝方法是在训练集上进行的,其效果怎么样呢?能解决过拟合问题吗?
艾博士:基于损失函数的剪枝方法需要调节一个合适的加权系数α,当α选择合适时,其效果还是不错的,可以得到一个比较好的决策树。
下面我们以图5.13建立的决策树为例,看看如何利用损失函数对决策树进行剪枝。为了方便计算我们将决策树重画如图5.16所示。
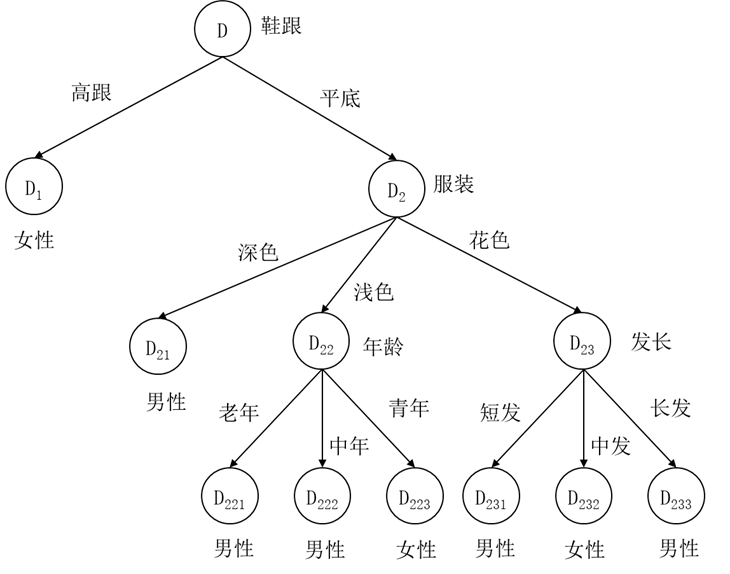
图5.16 男女性别分类决策树
首先我们计算剪枝前的损失函数,假设加权系数α为2。
该决策树共有8个叶节点,每个叶节点中的样本都是“纯的”男性或者女性,叶节点的熵均为0,所以损失函数第一项为0。第二项为α乘以叶节点个数。所以损失函数为:
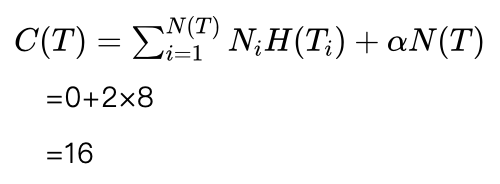
下面看看如果剪掉节点 D22 的所有子节点是否合理。剪掉节点 D22 的所有子节点后,决策树的叶节点数为6,除了叶节点 D22 外,其余叶节点没有变,这些叶节点的熵还是0。下面计算叶节点 D22 的熵。
根据前面的数据,叶节点D22 中共有4个样本,其中3个男性样本、1个女性样本,这样得到 D22 的熵为:

所以剪枝后的损失函数为:
这样剪枝后的损失函数15.2452小于剪枝前的损失函数16,所以这个剪枝是合理的,接受该剪枝,得到剪枝后的决策树如图5.17所示。其中由于叶节点 D22 中男性样本多于女性样本,所以类别标记为男性。
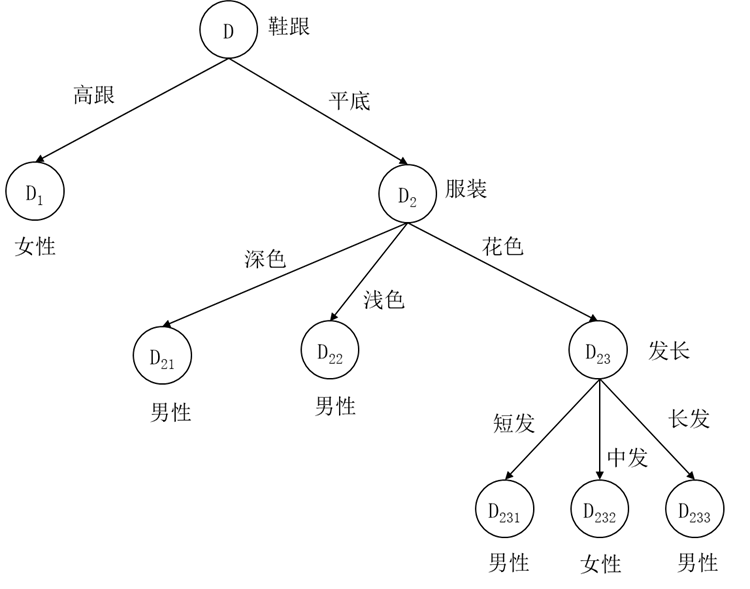
图5.17 第一次剪枝后的男女性别分类决策树
接下来再看看如果剪掉节点 D23 的所有子节点是否合理。剪掉节点 D23 的所有子节点后,决策树的叶节点数为4,我们已经知道叶节点 D1、D21 的熵为0, D22 的熵刚刚计算过结果为0.8113。下面计算叶节点 D23 的熵。
根据前面的数据,节点 D23 中共有2个样本,其中1个男性样本、1个女性样本,这样得到 D23 的熵为:

所以剪枝后的损失函数为:
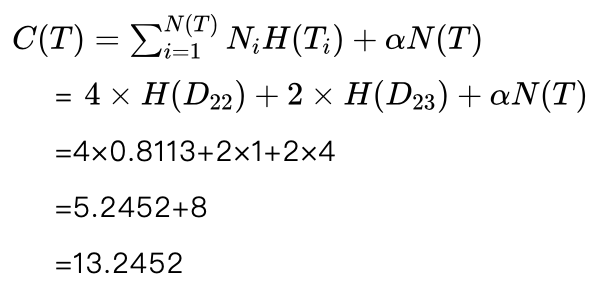
这样剪枝后的损失函数13.2452小于剪枝前的损失函数15.2452,所以这个剪枝也是合理的,接受该剪枝,得到剪枝后的决策树如图5.18所示。由于叶节点 D23 中男女样本各有一个,类别标记可以是男性也可以是女性,我们假定标注为女性。
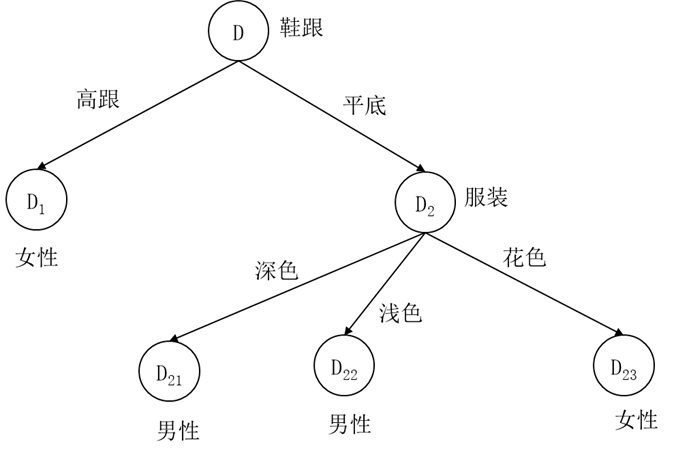
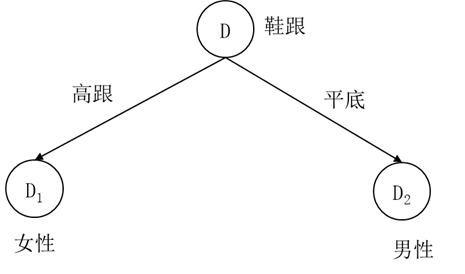
图5.18 第二次剪枝后的男女性别分类决策树
小明有些疑虑地问到:这里剪枝前的损失函数为什么是15.2452而不是16呢?
艾博士解释说:这里的“剪枝前”指的是对 D23 的子节点做剪枝前,也就是将 D22 的子节点剪掉之后的结果,不是最开始没有剪枝时的损失函数。
小明不好意思地说:我想错了,这个结果是对的。
艾博士继续讲解说:到这里为止,我们已经完成了两次剪枝,接下来还要看看节点D2 的子节点是否可以剪掉。
剪掉节点D2 的所有子节点后,决策树的叶节点数为2,我们已经知道叶节点 D1 的熵为0。下面计算叶节点D2 的熵。
根据前面的数据,节点 D2 中共有10个样本,其中8个男性样本、2个女性样本,这样得到 D2 的熵为:
H(D2 )=-(P(男性) log(男性)+P(女性) log(女性) )
=-(8/10 log(8/10)+2/10 log(2/10) )
=0.7219
所以剪枝后的损失函数为:
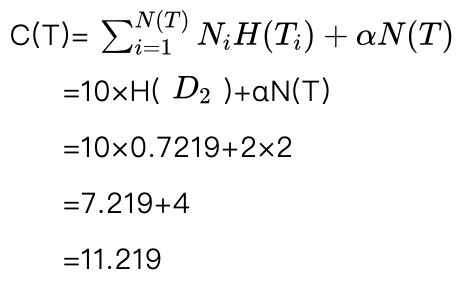
这样剪枝后的损失函数11.219小于剪枝前的损失函数13.2452,所以这个剪枝也是合理的,接受该剪枝,得到剪枝后的决策树如图5.19所示。由于叶节点 D2 中男性样本多于女性样本,所以叶节点 D2 标注为男性。
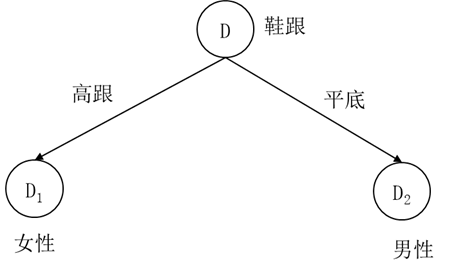
图5.19 第三次剪枝后的男女性别分类决策树
艾博士继续讲解说:到这里为止,我们完成了三次剪枝,接下来还要看看节点D的子节点是否可以剪掉。
剪掉节点D的所有子节点后,决策树的叶节点数为1,我们计算节点D的熵。
根据前面的数据,节点D中共有15个样本,其中8个男性样本、7个女性样本,这样得到D的熵为:
H(D)=-(P(男性) log(男性)+P(女性) log(女性) )
=-(8/15 log(8/15)+7/15 log(7/15) )
=0.9968
所以剪枝后的损失函数为:
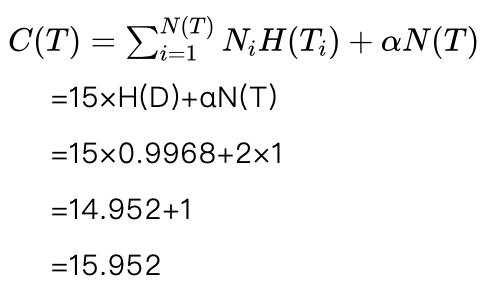
这样剪枝后的损失函数15.952大于剪枝前的损失函数11.219,所以这个剪枝不是合理的,拒绝该剪枝。
至此,不存在其他可能的剪枝了,剪枝过程结束,图5.19所示的决策树就是我们最后得到的决策树。由于这个例子数据并不多,其结果不一定典型,不要太在意最后的结果,我们只是通过这个例子演示剪枝的过程。
小明:我明白您的用意,通过这个例子也清楚地了解了具体的剪枝过程。
未完待续

