马老师教AI：第五篇统计学习方法是如何实现分类与聚类的（十）

第五篇统计学习方法是如何实现分类与聚类的（十）

清华大学计算机系马少平

第十节：线性支持向量机

小明：您前面介绍的支持向量机叫线性可分支持向量机，也就是说要求训练集中的样本必须是线性可分的。如果训练集不满足线性可分条件，比如说绝大部分样本可以用一个超平面分开，但是有少数样本不能被区分开，如图5.33所示两类样本交叉在一起的情况，无论怎么画直线也不能将两类分开，这种情况下还可以使用支持向量机方法构造一个分类器吗？

艾博士：前面我们介绍的是线性可分支持向量机，针对的是训练样本线性可分的情况。如果训练集中只有少数样本不具有线性可分性，其他绝对大部分样本都可以线性可分时，也可以构造支持向量机，只是这种情况下就不是线性可分支持向量机了，是线性支持向量机，少了“可分”二字。

小明：在线性可分支持向量机中，通过最大间隔求解最优分界面，当训练集不具有线性可分性时，如何求解最优分界面呢？

艾博士：我们先来回顾一下式(5.36)给出的线性可分支持向量机问题：

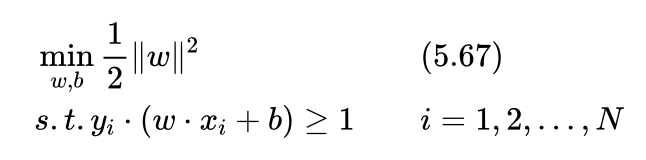
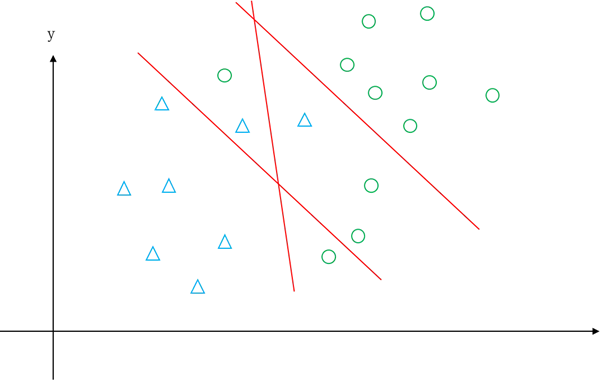
图5.33 两类样本出现交叉情况示意图

在该问题中，要求训练集中的所有样本到最优分界面的函数间隔均大于等于1，也就是满足条件：

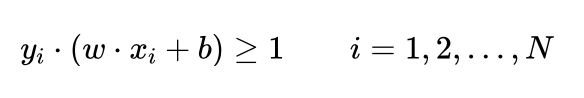
在训练集线性可分的情况下，可以做到这一点。当训练集不具有线性可分性时，就需要降低要求，弱化该条件，在大多数样本满足该约束条件的情况下，允许少量样本不满足该条件。这里的关键是如何衡量“允许少量样本不满足该条件”。

小明：那就是满足该条件的样本越少越好，以此为优化条件。

艾博士：当然这么做也不是不可以，但是不满足该条件也有程度上的不同。如图5.34所示，假设样本a到最优超平面的函数间隔为0.9，虽然不满足约束条件，但是也只是以微小差距不满足约束条件，样本b到最优超平面的函数间隔为0.1，显然二者不是等价的，如果在a与b中选择一个样本允许其不满足约束条件的话，我们会更愿意选择a而不是b。再看样本c，其不但不满足约束条件，还“跑”到了超平面的另一端，更是我们希望尽可能避免的。

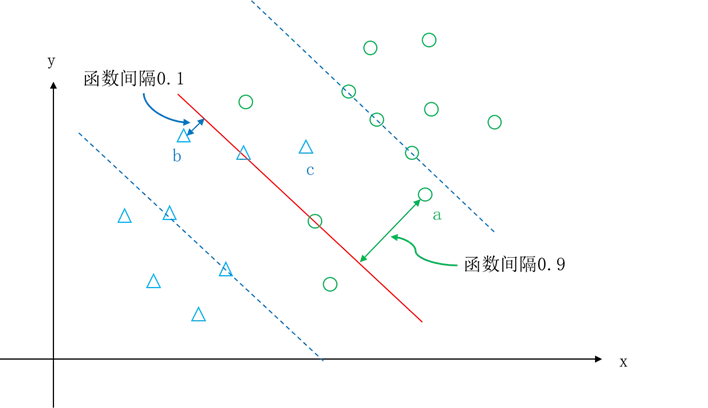
图5.34 不满足约束条件的样本示例

为此我们引入松弛变量 ξi>=0(i=1,2,...,N) ，每个样本 xi 对应一个 ξi=0 ，对于满足约束条件的样本 xi ，其对应的 ξi=0 。对于不满足约束条件的 xi ，我们允许该样本到超平面的函数间隔小于1，但是也不能太离谱，要求大于等于 1=ξi ，也就是式(5.67)中的约束条件修改为：

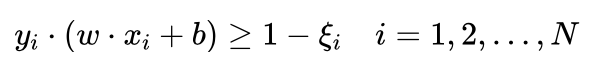
同时要使得所有的 ξi 之和尽可能小。

这样线性支持向量机就变成了求解如下的优化问题：

这就是线性支持向量机的优化问题，该问题同样可以采用类似于前面介绍过的拉格朗日乘子法，并转化为对偶问题求解，只有由于又引入了新的变量，变得更加复杂，我们就不做介绍了，直接给出其对应的对偶问题：

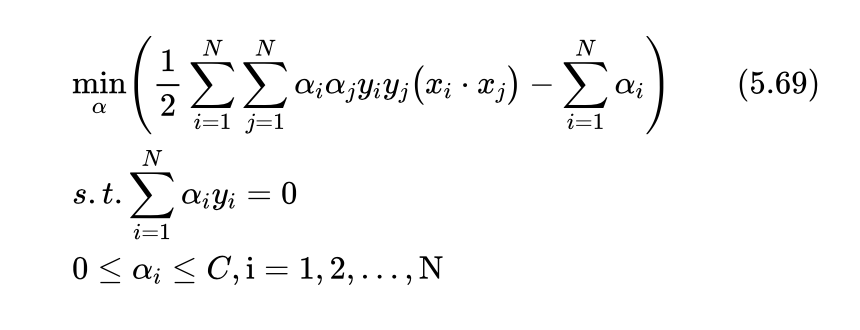
讲解到这里艾博士问小明：你看看式(5.69)所示的线性支持向量机对应的优化问题与我们前面讲的式(5.57)所示的线性可分支持向量机对应的优化问题有什么区别吗？

小明初看并没有发现有什么不同的地方，正想回答说没看出有哪些不同时，突然发现二者确实有少许差别，于是回答到：在式(5.57)中，αi 只要求大于等于0，而在这里要求是大于等于0，同时小于等于C。除此之外应该就没有其他方面的差别了。

艾博士称赞小明看得认真仔细：确实只有这一个小差别。也就是说，在线性可分支持向量机中，αi 的值可以任意大，但是在线性支持向量机中，αi 的变化受到限制，不能大于C的值，这里的C就是式(5.68)中的惩罚参数。可以设想，如果C接近于无穷大时，式(5.68)所示的最小值问题只能是 ξi 趋近于0，这时线性支持向量机就与线性可分支持向量机完全一样了，可见线性可分支持向量机是线性支持向量机当C趋近于无穷时的一个特例。

同样，满足式(5.69)最小值条件的α 我们记作 α*：

同样，与非零值 αi* 对应的样本就是支持向量，只是这里的支持向量有两类。一类是到最佳分界面的函数间隔等于1的样本，这是标准的支持向量，与这类样本对应的 ξi=0、0<αi*<C 。还有一类是到分界面的函数间隔小于1的样本，或者是“跑”到了最优分界面另一面的样本（即分类错误的样本），也被称作支持向量，与这类样本对应的 ξi>0 、αi*=C 。当 ξi=1 时，对应的样本刚好在最优分界面上，分类决策函数为0，无法判断其对应样本的类别；当 ξi<1 时，其对应的样本可以得到正确分类；当 ξi>1 时，其对应的样本被错分为另一类。与 αi*=0 对应的样本就是非支持向量，最优分界面与这些样本无关，在训练结束后可以将其从训练集中删除。

图5.35给出了一个支持向量与 ξi 之间的关系示意图。

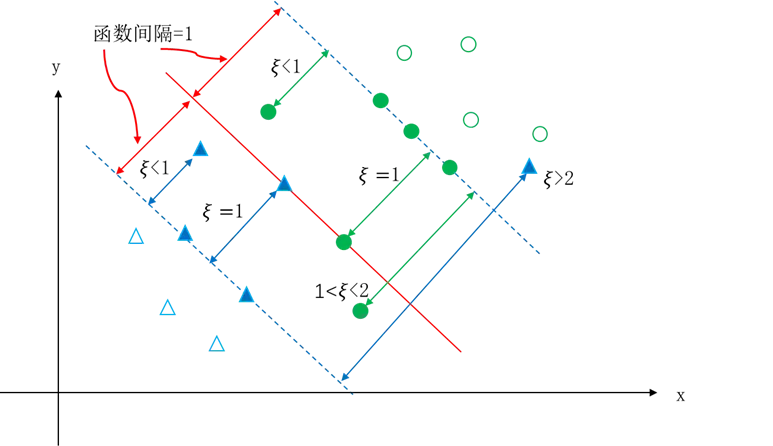
图5.35 支持向量与之间的关系示意图

图中实心样本点均为支持向量，空心样本点均不是支持向量。处于虚线上的三个绿色样本点和两个蓝色样本点，是标准的支持向量，他们到最优超平面的函数间隔为1，对应的 ξi 值为0，对应的αi* 满足 0<αi*<c 。ξ<1 对应的样本点，其分类正确，相应的 αi*=c 。ξ>1 对应的样本点，其分类错误，相应的 αi* =C。

小明：那么如何得到 ξi 的值呢？

艾博士： ξi 是引入的中间变量，线性支持向量机并不需要知道ξi 的值。如果想了解每个样本对应的 ξi 值，可以通过计算得到。首先αi*=0 对应样本点 xi 不是支持向量，其到最优分界面的函数间隔肯定大于1，所以对应的 ξi 其值也为0。其次，对于满足条件的，其对应的样本点是标准的支持向量，其到最优分界面的函数间隔等于1，所以对应的 ξi 其值也为0。只有所对应的 ξi 其值为一个大于0的数，其对应的 xi 也为支持向量，应满足条件：

对于分类正确的样本点，如图5.35中所示的 ξi <1 的样本点，其到最优分界面的函数间隔大于0小于1，所以自然有 ξi <1 。对于分类错误的样本点，如图5.35中所示的 ξi >1 的样本点，由于出现了分类错误，此时计算的函数间隔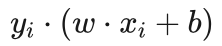是个负数，所以实际上相当于：

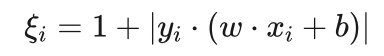
所以自然有 ξi >1 。

小明有些不解地问到：函数间隔为什么还可以是负数呢？

艾博士解释到：在分类正确的情况下，对于正类样本点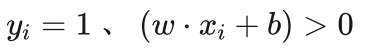，，对于负类样本点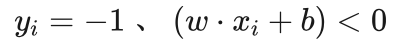，，所以无论是正类还是负类样本点，均有函数间隔大于0的结果。但是当分类错误时，比如对于标记为正类的样本点被错分成了负类，则 yi还是为1，但是计算得到的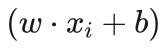会小于0，所以就出现了函数间隔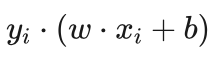小于0的情况。当标记为负类的样本点被错分成正类时，也会出现同样的结果。也正是由于这一点，对于错分类的样本点，我们也可以通过式(5.74)计算错分类样本点 xi 对应的 ξi 值。