第五篇 统计学习方法是如何实现分类与聚类的(九)
清华大学计算机系 马少平
第九节:线性可分支持向量机
艾博士:我们首先讨论最简单的线性可分支持向量机。
小明:线性可分支持向量机是个什么概念呢?
艾博士:对于给定的训练集 T=(x1,y1),(x2,y2),...,(xn,yn) ,如果采用该训练集求得的最优分界面可以将训练集中两类样本严格分开,则得到的支持向量机为线性可分支持向量机。其中的“线性”指的是采用超平面对样本进行分类,“可分”指的是用一个超平面可以将训练集中的样本无差错地分开。图5.29所示的就是一个线性可分支持向量机。
下面我们就看看当给定了一个线性可分的训练集后,如何求得一个线性可分支持向量机,也就是如何求得分类所需要的最优分界面。
前面我们曾经说过,最优分界面是使得到两个类别的距离中最小的距离最大的分界面,分解一下,这句实际上包含了两个意思:一是“到两个类别的距离中最小的距离”实际上就是训练集T到超平面的几何间隔γ ,由于γ 是所有样本点到超平面的几何间隔中最小的,也就隐含了满足条件“训练集T中所有样本点到超平面的几何间隔都要大于等于 γ ”;而“到两个类别的距离中最小的距离最大”表达的就是希望训练集T到超平面的几何间隔 γ 最大。通过这种求解最优分界面的方法我们称作间隔最大化。
综合上述两点,用数学语言表达就是:
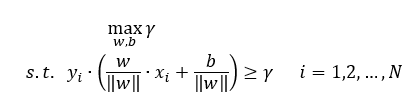 (5.33)
(5.33)
其中“s.t.”表示满足条件的意思,也就是说在满足这个条件下,求一个超平面使得 γ 最大。
上式中第一个数学表达式说的是求一个超平面(w,b)使得训练集到超平面的几何间隔 γ 最大,第二个不等式是说训练集中所有样本点到超平面的几何间隔要满足大于等于 γ 这个条件。
式(5.33)是用几何间隔描述的,根据式(5.29)、(5.32)给出的几何间隔与函数间隔的关系,式(5.33)也可以采用函数间隔 γ 描述如下:
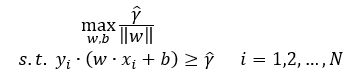 (5.34)
(5.34)
前面我们介绍过函数间隔的特点,可以任意进行缩放,所以为了描述简单,我们可以令 γ =1,这样式(5.34)就可以表述为:
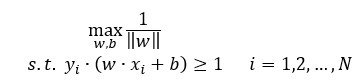 (5.35)
(5.35)
小明:原来函数间隔可以这么用,真是巧妙。这就相当于在满足约束条件 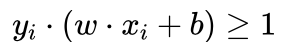 的情况下,求 1/||w|| 的最大值问题。那么如何求解这种具有约束条件的最大值问题呢?
的情况下,求 1/||w|| 的最大值问题。那么如何求解这种具有约束条件的最大值问题呢?
艾博士:直接求1/||w|| 的最大值有些难度。由于1/||w|| 最大与1/2||w||^2 最小是等价的,所以式(5.35)最大值问题可以转换成如下的最小值问题:
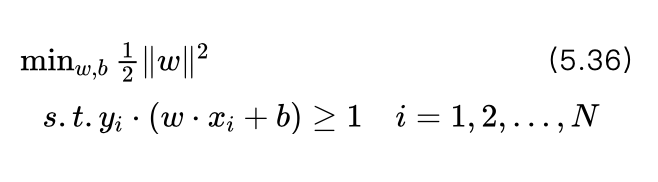
这就是线性可分支持向量机问题。
小明:这里为什么要乘上一个“1/2”呢?
艾博士:乘上一个常数并不影响其最小值的求解,这里乘上一个“1/2”主要是为了最终得到的结果形式更加简单。
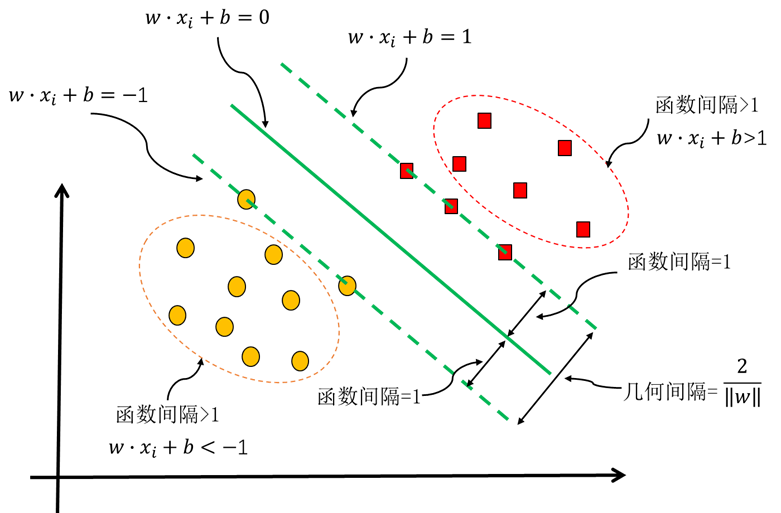
图5.30 线性可分支持向量机示意图
艾博士继续讲解说:图5.30给出了线性可分支持向量机的示意图,图中中间实线为超平面,其方程为 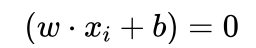 ,两条虚线方程分别为
,两条虚线方程分别为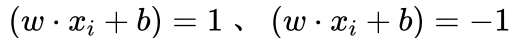 。虚线到超平面的函数间隔为1,虚线上的5个样本点为支持向量,它们到超平面的函数间隔均为1。其他样本点到超平面的函数间隔均大于1。两条虚线之间的函数间隔为2,根据函数间隔与几何间隔之间的关系,我们知道两条虚线之间的几何间隔为2/‖w‖ ,这也是训练集中两类样本间的最大间隔。
。虚线到超平面的函数间隔为1,虚线上的5个样本点为支持向量,它们到超平面的函数间隔均为1。其他样本点到超平面的函数间隔均大于1。两条虚线之间的函数间隔为2,根据函数间隔与几何间隔之间的关系,我们知道两条虚线之间的几何间隔为2/‖w‖ ,这也是训练集中两类样本间的最大间隔。
小明:是否按照式(5.36)求出最大间隔的超平面(w,b)就可以了?
艾博士:这是一个具有不等式约束的最优化问题,直接求解比较困难,一般是采用拉格朗日乘子法求解。拉格朗日乘子法是一种常用的求解这类具有不等式约束最优化问题的方法,在一般的最优化方面的书中都有介绍,我们不详细介绍该方法,直接给出如何用拉格朗日乘子法求解该最优化问题,并加以简单的解释。
为了构建拉格朗日函数,我们先对式(5.36)做一个简单的变换,写成如下形式:
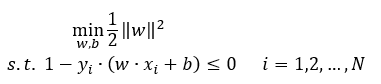 (5.37)
(5.37)

式(5.38)所示的拉格朗日函数由两部分组成,其中第一部分为式(5.37)中第一个表达式去掉“min”后的部分1/2||w||^2 ,第二部分为式(5.37)中不等式左边部分乘以拉格朗日乘子后再做累加和。
小明:这个拉格朗日函数与我们要求解的最优化问题有什么关系呢?
艾博士:下面我们简单分析一下这个问题,如果想详细了解其中的数学原理,请参看有关最优化问题的书籍。
我们看下图:
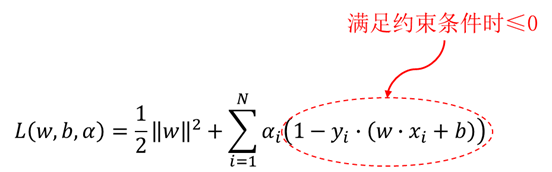
图中拉格朗日函数被红色虚线圈起来的部分为我们要求解的最优化问题的约束条件,由式(5.37),当满足约束条件时此项应该小于等于0,不满足约束时大于0。


我们希望得到的超平面应该满足不等式约束,所以就有:
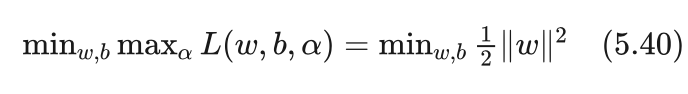
并且“自动”满足了不等式约束条件:
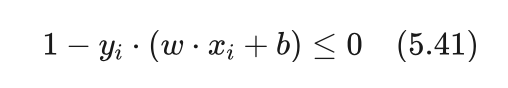
小明:拉格朗日乘子法真是太巧妙了,经过这样的转换后,就“消除”了不等式这个约束条件。但是,这里又引入了新的一组变量 ,并且需要求解一次最大化和一次最小化,是不是求解起来更加复杂了?
艾博士:粗看起来确实是更复杂了,且引入了更多的变量 α ,其分量 αi 的个数同训练样本一样多。但是由于“消除”了不等式约束条件这个“拦路虎”,变得复杂一些也是值得的,并且还存在简化的可能性。
小明:如何进行简化呢?
艾博士:我们先看看原问题:
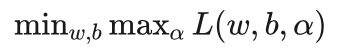
与其对偶问题:
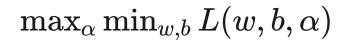
之间的关系。
小明:什么是原问题的对偶问题呢?
艾博士:简单地说,原问题是先求最大再求最小,其对偶问题就是反过来,先求最小再求最大。
小明:原来是这样的,您这么一说才发现您前面说的两个式子的不同。
艾博士:一般情况下,原问题与其对偶问题之间并不直接相等。比如我们举一个例子,假定一个班级同学中身高有高有矮,年龄有大有小,身高有相同的,年龄也有相同的。我们想求身高最高的同学中年龄最小的同学,也就是先对身高求最大,然后再对年龄求最小。其对偶问题就是年龄最小的同学中身高最高的同学。假设班上身高最高的同学是A、B,A的年龄大于B的年龄,则原问题的解为B同学。再假设C、D是班上年龄最小的两位同学,C的身高比D高,则原问题对偶问题的解是同学C。无论是从身高的角度还是年龄的角度来说,C都不会大于B。因为从身高角度说,B是身高最高的同学之一,所以C的身高不会比B高。从年龄的角度来说,由于C是年龄最小的同学之一,所以C的年龄也不会比B大。所以无论是说身高还是说年龄,都有C≤B,即:
身高最高的同学中年龄最小的同学≤年龄最小的同学中身高最高的同学
只有当C和B的身高、年龄都相等时等式才成立,这时C和B可能是同一个同学。
如果等式成立,我们就可以通过求解对偶问题的解得到原问题的解,前提条件是对偶问题更容易求解的话。
小明:这是一个很好的思路,就看对偶问题是否与原问题相等了。
艾博士:下面我们一步步分析一下这个问题。
拉格朗日函数显然满足下面这个不等式:
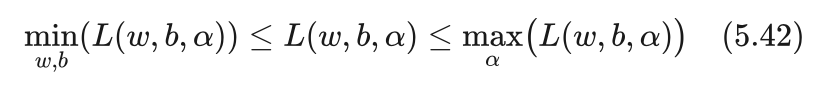
上式中,左边是以w、b为变量求最小值,拉格朗日函数显然应该大于等于该最小值;右边是以 为变量求最大值,同样拉格朗日函数显然应该小于等于该最大值。
由式(5.42)有:
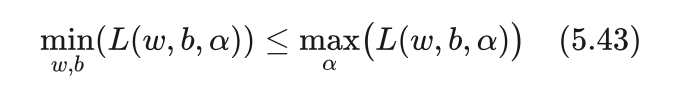
在任何取值下上式右边总是大于等于左边,那么右边的最小值也一定大于等于左边的最大值,所以有:
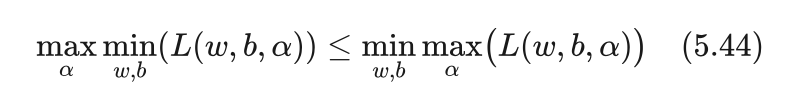
上式右边刚好就是原问题,左边是它的对偶问题。也就是说,原问题总是大于等于其对偶问题,这跟我们前面刚讨论的年龄、身高问题结论是一样的。
那么等号是否成立呢?只有当等号成立时,我们才可以用对偶问题求解原问题的解。可以证明,当问题同时满足KKT条件时,不等式(5.44)中的等式成立。
小明:那么什么是KKT条件呢?
艾博士:KKT条件是以三个提出者的姓氏首字母命名的,我们就不详细介绍为什么满足KKT条件时不等式(5.44)中的等式成立,只结合我们的具体问题,给出具体的KKT条件如下:
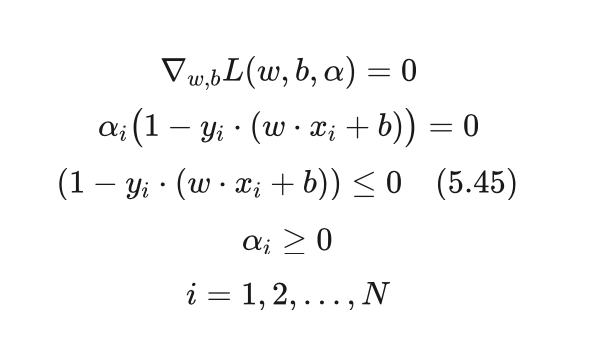
我们逐一分析一下这几个条件。

由于无论是原问题还是对偶问题都要求拉格朗日函数对w、b的最小值,梯度为0是最小值需要满足的必要条件。
接下来我们先看第三条 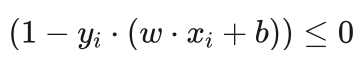 ,这是式(5.37)中的不等式条件,也是必须满足的条件。
,这是式(5.37)中的不等式条件,也是必须满足的条件。
再看第四条 αi>=0 , αi 是引入的拉格朗日乘子,要求大于等于0,所以也是必须满足的条件。
再回头看第二条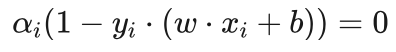 ,要满足这个条件只能是 αi=0 ,或者是
,要满足这个条件只能是 αi=0 ,或者是 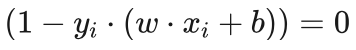 ,二者至少有一个为0。由KKT条件的第三条和第四条得知,这两个都有可能为0。当 αi 等于0时,
,二者至少有一个为0。由KKT条件的第三条和第四条得知,这两个都有可能为0。当 αi 等于0时,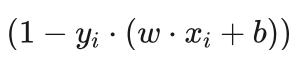 的值可以是任意值,当 αi 不等于0时,
的值可以是任意值,当 αi 不等于0时,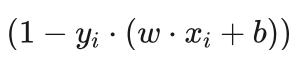 的值必须为0。同样当
的值必须为0。同样当 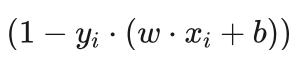 的值为0时, 的值可以是任意值,当
的值为0时, 的值可以是任意值,当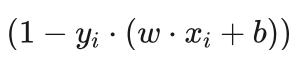 的值不为0时,αi 的值必须是0值。
的值不为0时,αi 的值必须是0值。
前面我们说过,支持向量到超平面的函数间隔为1,所以满足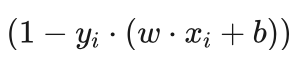 的值为0的 xi 刚好就是支持向量。由于每个拉格朗日乘子 αi 对应一个样本 xi ,由此也可以得知,不等于0的 αi 所对应的xi 就是支持向量。
的值为0的 xi 刚好就是支持向量。由于每个拉格朗日乘子 αi 对应一个样本 xi ,由此也可以得知,不等于0的 αi 所对应的xi 就是支持向量。
小明:原来拉格朗日乘子跟支持向量之间还具有这种关系。
艾博士:这样的话,如果同时满足KKT条件,不等式(5.44)就可以写为等式:

 从上式可以看出拉格朗日函数是w、b的二次函数,偏导数等于0处就是该函数的最小值点,我们可以令偏导数等于0,求出其极值点。而偏导数为0也刚好是应该满足的KKT条件中第一个梯度为0的条件。
从上式可以看出拉格朗日函数是w、b的二次函数,偏导数等于0处就是该函数的最小值点,我们可以令偏导数等于0,求出其极值点。而偏导数为0也刚好是应该满足的KKT条件中第一个梯度为0的条件。

 小明:明白了,这种情况下换了不同的下标表示起来确实比较方便,如果是相同的下标就不能这么写了。
小明:明白了,这种情况下换了不同的下标表示起来确实比较方便,如果是相同的下标就不能这么写了。
对式(5.54)做化简,并利用式(5.53)的结果,可以得到min┬(w,b)(L(w,b,α))的结果如下:

同时要满足条件(5.53)。
对式(5.56)括弧内部分增加一个负号,这样最大值问题就转化为了等价的最小值问题,即:
 小明:我们的目的是求解支持向量机的分界超平面,如何得到超平面呢?
小明:我们的目的是求解支持向量机的分界超平面,如何得到超平面呢?
艾博士:满足式(5.57)最小值条件的 α 我们记作 α* :
 小明看着这个结果有些不解地问到:上式中, yj 是不是应该是 1/yj 才对啊?
小明看着这个结果有些不解地问到:上式中, yj 是不是应该是 1/yj 才对啊?
艾博士:我猜测到你会问这个问题。在前面我们讲过,yj 是类别标记,在支持向量机中类别只有正类和负类,分别标记为1和-1,所以 yj 不是1就是-1,所以 yj=1/yj 。
小明恍然大悟到:对的,您当时还特别强调一定要我记住这一点,说后面推导中会用到,我还是给忘记了。
艾博士:在开始学习时这是很正常的,以后记住就可以了。
艾博士继续讲解到:根据式(5.59)就得到了超平面方程:

前面我们曾经讲过,与非零的 αi* 对应的xi 就是支持向量,从上式也可以看出,分类决策函数只与训练集中的支持向量有关,对于非支持向量,由于其对应的αi* 等于0,不影响分类决策函数。
小明:这样的话,当支持向量机训练结束后,只需保留那些支持向量和相应的非零 αi* 就可以了。
艾博士:小明你说很对,支持向量机最终的结果只与支持向量有关,而与非支持向量无关,那些非支持向量就不需要再保存了。
下面我们给一个根据训练集样本求解支持向量机的例子。
 为方便计算,我们先计算好几个样本点的点积:
为方便计算,我们先计算好几个样本点的点积:

 这样对偶问题就变成了求s对α1 、α2 的最小值问题。由于s是关于α1 、α2 的二次函数,是一个凸函数,所以其最小值在偏导数等于0处,可以通过计算s对α1 、α2 的偏导数,并分别令其为0求解。
这样对偶问题就变成了求s对α1 、α2 的最小值问题。由于s是关于α1 、α2 的二次函数,是一个凸函数,所以其最小值在偏导数等于0处,可以通过计算s对α1 、α2 的偏导数,并分别令其为0求解。

讲解到这里艾博士问小明:这样得到的 α1、 α2是不是就是我们想要的结果呢?
小明见艾博士这样询问,心想这里一定有什么问题,想到:s是关于α1 、α2 的二次函数,是个凸函数,最小值一定出现在偏导数等于0的地方,应该没有问题啊?艾博士为什么这么问呢?
小明边想边查看前面讲解的内容,突然醒悟到:由于对偶问题要求满足条件α1>=0 、α2>=0 ,而这个结果中 α1=-4 ,并不满足 α1大于等于0的条件。
艾博士夸奖说:小明你说的非常正确,如果α1 、α2 都满足大于等于0的条件,则这个结果就是我们希望得到的结果,但是这里求得的 α1 不满足大于等于0的条件,虽然我们求得的确实是s的最小值,但是不是满足约束条件的最小值。如何得到满足约束条件的最小值呢?我们看一下单变量的情况,单变量看起来更加直观。
假设f(x)是x的二次函数,其图象如图5.31所示。f(x)在x=x0处取得最小值a,但是如果要求x大于等于0的话,满足要求的f(x)的最小值在x=0处取得,其值为b。也就是说,如果函数的实际最小值不在我们要求的定义域范围内,则满足要求的最小值应该发生在定义域的边界处,也就是x=0的地方。函数是多变量时,也有类似的结论,只是对于多变量的情况,每个变量都有一个边界,需要计算出每个边界下函数的最小取值,取其中最小的一个就是我们所要求解的最小值。前提条件是函数是一个凸函数,而二次函数刚好是凸函数。
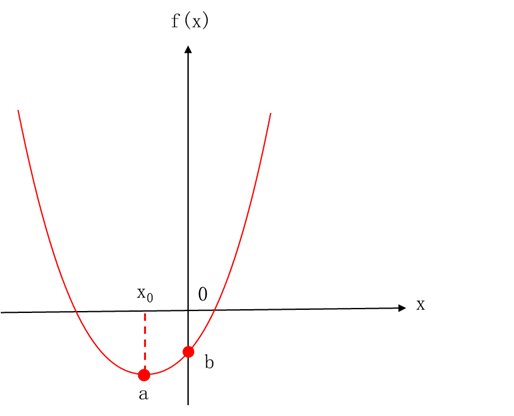
图5.31 二次函数最小值示意图
艾博士继续讲解到:我们再回到例题中来,由于是负的,不满足我们的要求。按照上述讨论,就要分别计算 α1=0 和 α2=0 两个边界条件下,s的最小值,然后取其中一个最小的结果作为解答。
小明问到:刚刚求解的 α2 其值为6,满足大于等于0的条件,也要计算这个边界下s的值吗?
艾博士肯定地说:是的,只要有一个αi 的取值不满足条件,就要计算每个 αi=0 时s的最小值,以便从中选择一个最小的结果。
下面我们分别计算两个边界条件下s的最小值。




 式(5.66)就是该例题的最优分界超平面方程,如图5.32所示。
式(5.66)就是该例题的最优分界超平面方程,如图5.32所示。
容易验证,由于样本 x2、 x3为支持向量,它们到该超平面的函数距离均为1, x1 不是支持向量,其到该超平面的函数距离大于1,等于 9/5 。
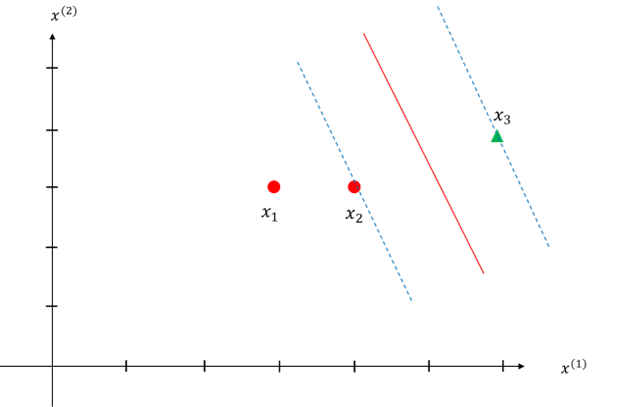
图5.32 例题的分界超平面示意图
由式(5.66)最优分界超平面方程,可以得到支持向量机的决策函数为:
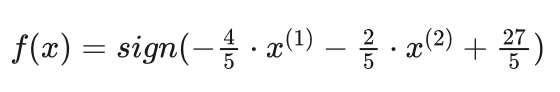
将例题中的待分类样本x=(1,1)带入到决策函数中:
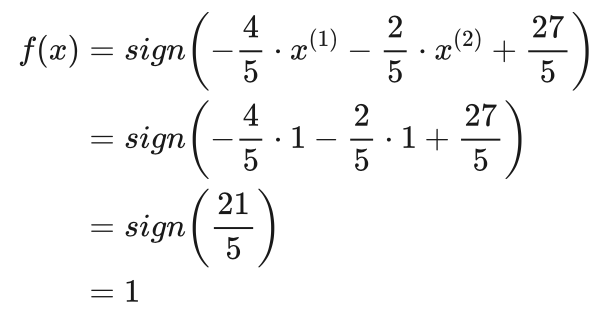
由此可知,待分类样本x=(1,1)的类别为正类。
未完待续

