第五篇 统计学习方法是如何实现分类与聚类的(十一)
清华大学计算机系 马少平
第十一节:
非线性支持向量机
小明:前面讲解的,无论是否线性可分,都是线性支持向量机,也就是求解一个最优超平面,将两类样本分开。但是有些情况下样本的分布可能比较复杂,用超平面很难将两类的大部分样本分开,是不是有非线性的支持向量机呢?我想既然不能用超平面分类,那就采用超曲面呀,在二维的情况下就是曲线。
艾博士:这就是我们下面将要讲解的非线性支持向量机。
请看图5.36所示,“○”形是一个类别,“△”形是一个类别。在这种情况下,不可能用一条直线将大部分样本正确分开。但是用如图所示红色的椭圆就可以将两个类别正确分开。这是从分界面是曲面的角度思考问题,能否从另一个角度思考一下这个问题呢?就是做一个非线性变换,使得在原来空间不能用超平面分类的样本,经过变换后,在新的空间中可以用超平面分类了。
小明:如果能做到这一点就好办了,因为在新的空间就可以使用线性支持向量机了,除了增加一个非线性变换以外,与前面讲过的线性支持向量机应该没有什么本质的区别。
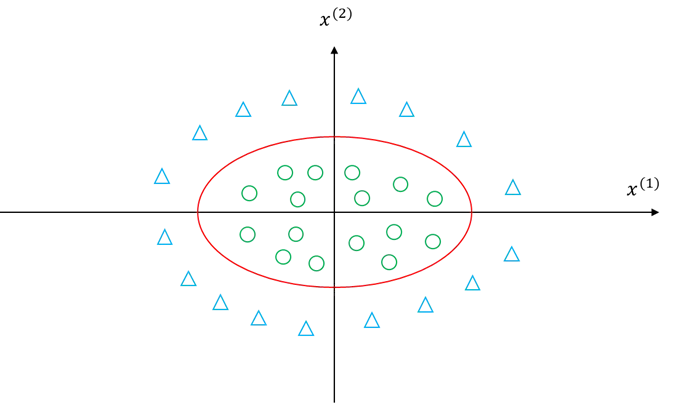
图5.36 非线性分类示意图

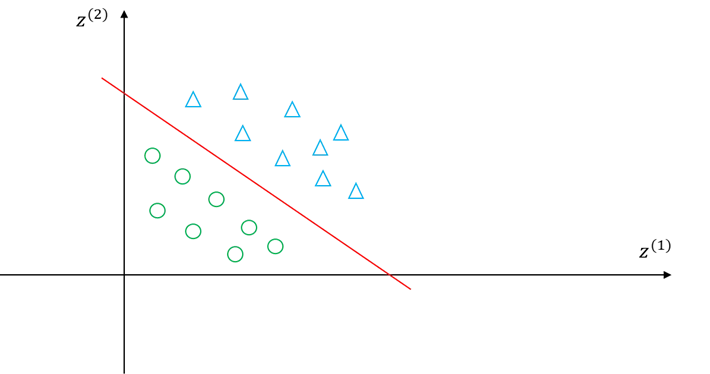
图5.37 变换后新空间样本分布示意图
这样就如同刚才小明说的,在新空间中就可以使用线性支持向量机方法求解最优分界面了,只需要将∅(xi) 代替 xi 作为训练样本就可以了。也就是将式(5.69)给出的线性支持向量机所对应的优化问题:

同样,我们可以得到在变换后新空间的最优分界超平面方程为:

小明:感觉非线性支持向量机的难点问题就是如何定义变换函数∅(x),一旦有了变换函数∅(x),非线性支持向量机的求解就与线性支持向量机求解完全一样了。
艾博士:一般是通过升维的办法定义变换函数∅(x),因为在n维空间如果不能实现线性可分的话,升维到更高的维度就可能实现线性可分了。我们给一个具体的例子。
设 x1=(0,0)、x2=(1,1) 属于正类,x3=(1,0) ,x4=(0,1) 属于负类,如图5.38所示。很显然在二维平面上该问题不可能用一条直线将两个类别分开。
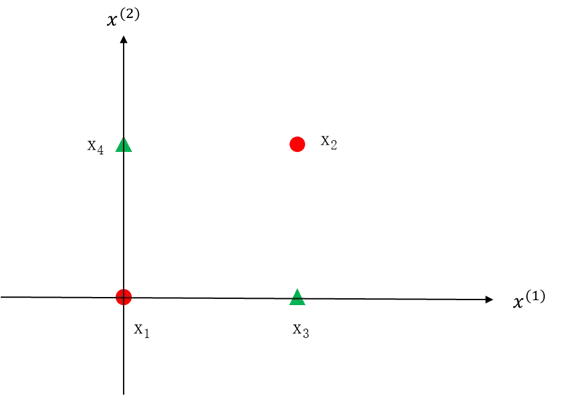
图5.38 线性不可分样本示意图
但是如果我们通过一个变换,将该问题升维到3维空间,结果会如何呢?

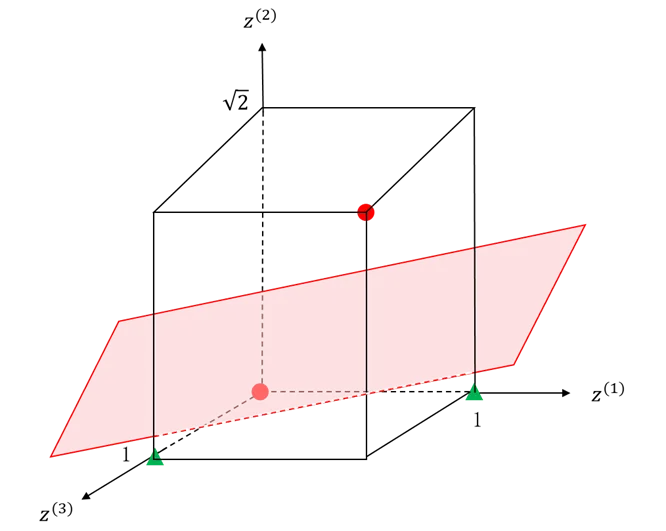
图5.39 变换后在三维空间的示意图
理论上可以证明,对于分布在n维空间上的两类样本点,总可以找到一个更高维的空间,在该高维空间上两类是线性可分的。不过这个更高维的空间其维度可能比原空间高很多维,甚至可能是无穷维的。
虽然可以通过升维的办法实现线性可分,但是如何定义变换函数∅(x)是一个比较困难的问题,因为实际问题中样本的分布可能非常复杂,以至于很难定义一个变换函数∅(x),使得变换后的训练集是线性可分的,或者训练集中的绝大部分样本是线性可分的。
小明:这样的话,非线性支持向量机不就没有任何实际意义了吗?
艾博士:小明你别着急,要相信科学家们的能力,他们经过不懈努力,终于提出了一种称作核方法的方法,非常完美地解决了这个问题。下面我们首先介绍一下什么是核方法。
未完待续

