第四篇 如何用随机算法求解组合优化问题（五）
清华大学计算机系 马少平
第五节：模拟退火算法
小明：如何利用退火过程的这些现象，改进局部搜索算法呢？
艾博士：在退火过程中，遇到一个高内能状态时，会以一定的概率转移到该状态，相当于在局部搜索中以一定的概率接受差解，这正是解决局部搜索算法中存在局部最优值所要采用的改进策略。模拟退火算法也正是要借鉴退火过程中的这个现象，改进局部搜索算法。为此首先我们要将组合优化问题与退火过程做个类比，之后就可以给出算法了。
表4.1给出了组合优化问题与退火过程的类比关系。
表4.1：组合优化问题与退火过程的类比
设S是某组合优化问题所有可能解的集合，集合S中任一元素i是该问题的一个解，f(i)是解i的指标函数。由表4.1给出的类比关系，i对应物理系统的一个状态，f(i)对应该状态的内能E(i)。与温度T对应的是一个控制参数t，用于控制算法的进程，其值随算法进程缓慢递减，最终接近于0。退火过程中粒子的热运动则用解在邻域中的交换来代替。这样就将一个组合优化问题与退火过程建立了对应关系。
在求解组合优化问题时，首先给定一个比较大的t值，这相当于在退火过程中首先将物体加热到很高的温度。然后随机给定一个问题的初始解i，随机从i的邻域中选择一个新解j。
讲到这里，艾博士问小明：那么如何接受这个新解j呢？
小明回答说：按照标准的局部搜索算法，只有当新解j好于解i时，才会接受新解j。但是这样会存在局部最优值问题。按照改进局部搜索算法的思路，应该随机地接受一些差解。
艾博士：正是这样的。如何随机地接受一些差解呢？这正是我们要向退火过程“学习”的地方。
我们前面讲过，在退火过程中按照Metropolis准则接受新状态：
如果E(j)≤E(i)，则状态转换被接受；
如果E(j)＞E(i)，则状态转移被接受的概率为：
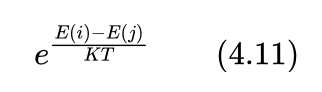
Metropolis准则表明，如果新状态的内能小于等于当前状态，则100%地接受该状态，如果新状态的内能大于当前状态，则按照概率接受。如果我们求解问题的最小解，则新状态的内能小于等于当前状态，相当于遇到了一个好解，这时马上接受该状态。否则就相当于遇到了一个差解，按照概率接受该状态。按照这样的准则，退火过程可以以概率1达到内能最小的状态。这不正好是我们希望改进后的局部搜索算法所要达到的效果吗？
小明：是啊，正是我们希望的效果。
艾博士：在退火过程中，K＞0是波尔兹曼常数，温度T是控制退火过程的变量。而对于局部搜索算法来说，可以将KT一并表示为控制参数t，因为波尔兹曼常数K对于算法来说没有任意意义，但是我们仍然称其为Metropolis准则。按照Metropolis准则我们可以得到从解i到新解j的接受概率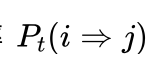 
为：
这样我们就可以得到一个改进的局部搜索算法。首先随机产生一个解i，从解i的邻域中随机选择一个新解j，按照Metropolis准则，如果新解j被接受，则以解j代替解i，否则继续保持解i。重复该过程，直到在该控制参数t下达到某种平衡。然后与退火过程中的温度T缓慢下降相对应，在进行足够多的状态交换之后，控制参数t需要缓慢下降，并在每个参数t下，重复以上过程，直到控制参数t降低到足够小为止。最终我们将以大概率求得该组合优化问题的最优解。由于该算法是通过模拟退火过程得到的，所以被称为模拟退火算法。
下面，我们给出模拟退火算法的具体描述。
模拟退火算法：
1、随机选择一个解i，k=0， t0=Tmax（初始温度），计算指标函数f(i)。
2、t=tk ,如果满足结束条件，则转（15）。
3、Begin
4、如果在该温度内达到了平衡条件，则转（13）。
5、Begin
6、从i的邻域N(i)中随机选择一个解j。
7、计算指标函数f(j)。
8、如果f(j)≤f(i)，则接受j，i=j，f(i)=f(j)，转（4）。
9、否则计算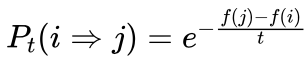 
10、如果 ,则接受j，i=j，f(i)=f(j)。
11、转（4）
12、End
13、对t降温，tk+1=Drop(tk) ，k=k+1，转（2）。
14、End
15、输出结果。
16、结束。
艾博士解释说：该算法有内外两层循环。内循环模拟的是在给定温度下系统达到热平衡的过程。每次循环随机地从解i的邻域中随机选择一个新解j，然后按照Metropolis准则，如果新解j比解i好，则100%接受新解j；如果新解j不如解i，则按概率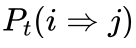 
接受新解j。
小明：在算法中如何实现按概率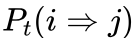 
接受新解j呢？
艾博士：在本篇4.3节讲解如何解决局部最优问题时曾经介绍过，这里我们就不再详细讲解了，课后你可以再去看看。这里主要利用一个[0,1]间均匀分布的随机数函数Random(0,1)随机产生一个[0,1]间的随机数，如果该随机数小于接受概率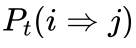 
，则接受差解j，否则就不接受。
小明：我想起来了，是曾经讲过，等下课后我再复习一下。
艾博士：算法的外循环模拟的是温度的下降过程。控制参数 起到与温度T相类似的作用，表示的是第k次循环时系统所处的温度。算法中的Drop(tk) 是一个温度下降函数，它按照一定的原则实施温度的缓慢下降，直到当 趋近于0时算法结束。
模拟退火算法与局部搜索算法很相似，二者最大的不同是模拟退火算法按照Metropolis准则随机的接受一些差解，即指标函数值大的解。当温度比较高时，接受差解的概率比较大，在初始高温下，几乎以接近100％的概率接受差解。随着温度的下降，接受差解的概率逐渐减少，直到当温度趋近于0时，接受差解的概率也同时趋近于0。这样采用类似于退火过程的方法，将有利于算法跳出局部最优解，大概率求得问题的全局最优解。
小明：谢谢艾博士，我大体上明白了模拟退火算法的计算过程。但是算法中还是有些不确定的描述，比如内循环中的“在该温度达到了平衡条件”，什么是平衡条件呢？外循环的“如果满足结束条件”，什么情况下满足结束条件呢？还有初始温度如何设置？温度又是如何下降的？这些算法中都没有说明啊。
艾博士：很高兴你提出这样的问题。上述模拟退火算法只是给出了一个算法的框架，其中重要的四个条件：初始温度的选取，内循环的结束条件、外循环的结束条件和温度如何下降，算法中都没有提及，而这正是模拟退火算法的关键所在。正像前面叙述过的那样，对于退火过程来说，要最终使得物理系统以概率1处于内能最小的一个状态，在退火过程中必须满足以下三点：
（1）初始温度必须足够高；
（2）在每个温度下状态的交换必须足够充分；
（3）温度T的下降必须足够缓慢。
这三点刚好与算法中未提及的4个重要条件有关。与退火过程一样，为了使得模拟退火算法以概率1求解到问题的最优解，则至少也要满足这三点。理论上来说，初始温度越高越好，温度下降的越慢越好，每个温度下交换的次数越多越好。然而这将严重降低算法的求解效率。但是如果不能满足这几点要求的话，也会影响算法求解最优解的效果，可能会得不到一个比较好的解。如何在求解效率与求解效果之间做一个平衡？也是模拟退火算法必须考虑的问题。就好比我们前面做弹簧的实验中，我们将钢丝加热到通红就可以了，没有必要再进一步加热。降温时，也是在室温中慢慢降温就可以了，也没有必要弄一个保温箱控制其温度的下降速度。同样的，温度也是降低到室温就满足要求了。因为我们的目的是做一个弹簧，只要处理后的钢丝柔软到我们可以方便加工就可以了，而不是必须让钢丝达到最软的程度。就如同我们前面曾经举例说过的买西瓜的例子，我们只需买一个吃起来满意的西瓜就好了，而不是必须购买一个世界上最甜的西瓜。在模拟退火算法中会综合考虑这些因素，有一些指导性的设置这些参数的方法。有关内容我们留待下一节再专门介绍。
小明：艾博士，模拟退火算法有哪些性质呢？
艾博士：下面我们就分析一下模拟退火算法的性质。
在模拟退火过程中，给定温度下状态（解）的转移可以看作是一个马尔可夫链。对于任意两个状态i和j，能否从状态i转移到状态j呢？这需要两个条件，一个条件是能否从状态i产生出状态j，以及从i产生j的概率是多少，简单说就是j是否是i的邻居，如果是邻居，有多大的概率能从i的邻域中选中j。另一个条件是，当j被选中时能否被接受，这与从i到j的接受概率有关。所以从i转移到j的概率就是从i产生j的概率乘以从i到j的接受概率。我们用 Pt(i,j) 表示温度t下，从状态i转移到状态j的一步转移概率，则有：
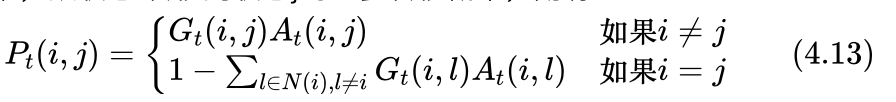
其中Gt(i,j) 是产生概率，表示从状态i产生状态j的概率。如果在邻域内等概率选取的话，领域外的状态被产生的概率为0，领域内的状态被产生的概率为领域大小分之一。即：
At(i,j) 是接受概率，表示在状态i产生状态j后，接受状态j的概率。如按照Metropolis准则的接受概率为：
在定义的邻域满足一定条件情况下，可以证明，这样得到的马尔可夫链其平稳分布唯一存在，在给定的t下，经过足够多次的转移之后，得到状态i的概率为：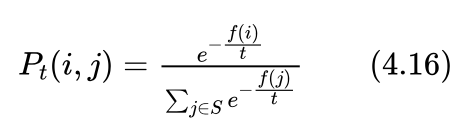 
该式与退火过程中的式（4.2）基本一致，仿照前面对退火过程类似的分析，我们有：
其中 Sm 表示满足最优解的状态集合，|Sm| 表示最优解的个数。也就是说，当温度t趋近于0时，模拟退火算法将以等概率得到多个最优解中的一个，其概率为最优解个数分之一。如果算法的目的就是求得一个最优解的话，则获取最优解的概率为1。即：
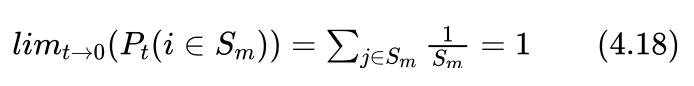
以上结果说明，只要在每个t下进行足够多次的状态转移，使得达到式（4.16）所示的平衡分布，当控制参数t缓慢地趋近于0时，则模拟退火算法将以概率1得到问题的全局最优解。
小明：艾博士，应该如何理解这里的“以概率1获得最优解”呢？
艾博士：模拟退火算法由于具有一定的随机性，每次求得的结果可能是不一样的，也有可能陷入某个局部最优解，所以也就不能保证每次运行都能获得最优解，但是获得最优解的概率是很大的。如果算法多次运行，则几乎可以找到最优解。当然前提条件是算法设置了合适的参数。
小明：艾博士，我又想到了一个问题。在开始介绍模拟退火算法的时候，您曾经提到模拟退火算法是为了解决局部搜索算法存在的前两个问题——局部最优值问题和变步长问题而提出来的改进算法。为解决局部最优值问题，模拟退火算法按照退火现象中的Metropolis准则以一定的概率接受差解。这一点算法中体现的很明显。但是模拟退火算法是如何体现变步长的呢？算法中似乎没有看到这一点。
艾博士：小明提出了一个很好的问题。我们还是以爬山法为例说明变步长问题。在爬山法中，步长可以认为就是拐杖的长度。拐杖越长所选择的范围就越广，变步长就相当于改变拐杖的长度。对于组合优化问题来说，没有一个直观的“步长”概念，大的步长可以认为是邻域比较大，可选择的新状态比较多，而小步长则相反，可以认为是邻域比较小，可接受的新状态比较少。而变步长就相当于在求解过程中，逐步缩小邻域的范围。在模拟退火过程中，当温度比较高时，从一个状态几乎可以转移到任何其他状态，相当于步长比较大，而随着温度缓慢降低，处于低内能状态的概率加大，从低内能状态转移到高内能状态的概率逐渐减少，就相当于逐步缩小了邻域范围。当然这里并不是真的缩小了邻域范围，而是通过逐渐减小接受概率的方式达到缩小邻域范围的目的，是一种“软”的变步长方法。不知道小明是否明白了这个道理。
小明歪着小脑瓜思考了一会说：我终于明白了，模拟退火算法中的“变步长”是通过概率方式改变“步长”的，相当于拐杖还是那个拐杖，但是能探索的范围是受概率控制的。刚开始时可以随便用拐杖进行探索，但是慢慢地拐杖探索的范围按照概率向身边收缩，能探索到远处的概率越来越小，而越靠近身边的近处探索概率越来越大，相当于拐杖变短了。
小明读书笔记
受退火现象的启示，将组合优化问题与退火过程建议对应关系，提出了模拟退火算法。组合优化问题的解对应物理系统的状态，解的指标函数对应状态的内能，最优解对应内能最低的状态，而控制参数则对应温度。
模拟退火算法完全模拟退火过程，并像退火过程那样以概率接受差解，从本质上来说，模拟退火算法就是一个改进的局部搜索算法，包括两点：一是以概率接受差解，二是变步长。这里的变步长是以概率形式体现的“软”步长，随着温度的降低，接受差解的概率越来越小。
可以证明，在初始温度足够高、在每个温度下交换足够充分、温度下降足够缓慢的条件下，将以概率1求解到最优解。
未完待续