第三篇 计算机是如何找到最优路径的(九)
清华大学计算机系 马少平
第九节:总结
最后,在艾博士的建议下,小明对本篇内容做了一个总结:
首先介绍了路径搜索问题的基本概念,以如何去香山举例说明了什么是路径搜索问题,很多问题也可以转化为路径搜索问题求解,比如八数码问题。
介绍了什么是宽度优先搜索算法,在宽度优先搜索算法中,优先选择节点深度最浅的节点扩展,通过例子讲解了宽度优先搜索算法的具体求解过程。当问题为单位代价时,也就是任何相邻的两个节点间的代价为1时,宽度优先搜索算法可以找到最优路径,也就是代价最小的路径。
宽度优先搜索算法只利用了节点的深度信息,而没有利用从初始节点到达待选择节点的路径代价。迪杰斯特拉算法充分利用了这一点,选择从初始节点到待选择节点路径最短的节点优先扩展。当被选择的节点是目标节点时算法结束,此时找到的到达目标节点的路径为最短路径。即便是非单位代价时,迪杰斯特拉算法也总是可以找到最优路径。这里一定要注意迪杰斯特拉算法的结束条件,必须是被选择扩展的节点是目标节点时算法才结束,而不是只要找到了一条到达目标节点的路径就立即结束,否则不能保证找到的是最佳路径。
迪杰斯特拉算法虽然用到了到节点的路径代价,但是并没有利用从一个节点到目标节点路径的代价,从而导致搜索效率低下,扩展过多的无用节点。但是一般情况下我们并不知道一个节点到目标节点的路径代价,A算法采用估计的方法估计出一个节点到目标节点的代价。定义节点n的评价函数f(n)=g(n)+h(n),其中g(n)为从初始节点到达节点n的路径代价,h(n)为从节点n到达目标节点最优路径代价的估计,f(n)为从初始节点经过节点n到达目标节点最优路径代价的估计。A算法优先选择f(n)最小的节点扩展,当目标节点的f值最小时,算法结束。注意,A算法的结束条件同迪杰斯特拉算法一样,必须是当被选择扩展的节点是目标节点时算法才结束。
在A算法中,对h函数并没有具体的要求,只是说是从节点n到目标节点路径代价的估计值。在A算法中,如果对于任何节点n要求h(n)≤h*(n),则A算法就成为了A*算法,其中h*(n)为节点n到目标节点最佳路径的代价。从算法描述的角度,A*算法与A算法是完全一样的,只是A*算法要求满足A*条件h(n)≤h*(n)。当问题有解时,A*算法可以保证找到最优解结束。
对于同一个问题,如果定义了两个满足A*条件的h函数h1 和 h2 ,那么如何评价哪个h函数更好呢?有定理保证,对于除了目标节点的任何节点n,如果总有 h2>h1 ,则采用 h2 的A*算法扩展的节点数不会多于采用 h2 的A*算法扩展的节点数。也就是说,采用 h2 时的效果不会比采用 h1 时差。由于两个h函数都满足A*条件,所以越大的h函数其对最佳路径代价的估计越准确,该定理说明采用更准确的h函数效果不会变差,所以应该尽可能定义更好的,也就是更准确的h函数。
还可以通过实际测试的方法评价两个不同的h函数的效果。定义状态搜索树的平均分叉数,通过实际实验,计算出采用不同的h函数时得到的平均分叉数,平均分叉数越小说明h函数的效果越好。
A*算法存在可能重复扩展节点的问题。当h函数定义不合理时,就可能会造成这种情况,从而降低算法的求解效率。如果h函数满足单调条件,则A*算法不会出现重复扩展节点的问题。h函数满足如下条件时,则称h函数是单调的:
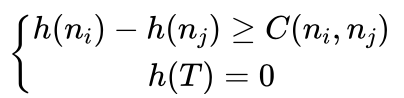
其中T为目标节点,ni 是 nj 的父节点,C(ni,nj) 是ni 、nj 间的代价。
当h函数不满足单调条件时,也可以通过修改A*算法的方式,减少重复节点扩展。设 fm 为目前为止扩展的节点中f函数的最大值。在改进的A*算法中,对于OPEN表中f值小于 fm 的节点,放入到NEST中,如果NEST中存在节点,则优先选择NEST中g值最小的节点优先扩展,当NEST中没有节点时,同A*算法一样,选择OPEN中的第一个节点扩展,并修改fm值为该节点的f值,其他均与A*算法一致。改进后的A*算法可以有效减少节点的重复扩展。
同宽度优先搜索算法相反,深度优先搜索算法每次优先选择节点深度最深的节点扩展,一般要加上深度限制和对循环路径的检测,以便防止搜索过程中陷入深渊或者死循环。深度优先搜索算法的最大特点是占用空间少,只需要记录从初始节点到当前节点的路径即可。为了解决宽度优先搜索算法、A*算法存在的占用空间过大问题,将深度优先搜索算法与这些算法结合,就有了迭代加深式搜索算法,包括迭代加深式宽度优先搜索算法和迭代加深式A*算法。这类算法的特点是既保留了深度优先搜索占用空间少的特点,又可以象宽度优先搜索算法、A*算法一样,找到问题的最优解。不足是会花费更多的搜索时间。
动态规划是求解决策过程最优化的一种方法,Viterbi算法是其中一种常用的算法,特别适合求解篱笆型有向图最短路径问题。从本质上来说,Viterbi算法与h=0时的A*算法是等价的,但是对于一类特殊问题,具有比较高的求解效率,具有非常广泛的应用。Viterbi算法从左到右一列一列地递推计算到达每个节点的最优路径,充分利用已有的求解结果,从而提高求解的效率。
最后列举了一个拼音输入法问题作为应用举例。通过利用贝叶斯公式以及一些必要的推导过程,可以将拼音输入法问题转化最优路径求解问题,利用语料库统计获得任意两个汉字之间的连接概率 p(wi|wi-1) ,并用 -log(p(wi|wi-1)) 表示两个汉字之间的代价,这样,利用Viterbi算法通过求解最短路径问题就可以得到给定拼音串对应的概率最大的句子。
《计算机是如何找到最优路径的》篇完结

