第四篇 如何用随机算法求解组合优化问题(一)
清华大学计算机系 马少平
艾博士导读
在实际问题中经常遇到求解给定约束条件下的最佳解问题,当可能解的数量是有限个时这类优化问题被称为组合优化问题。由于组合优化问题可能解的数量是有限个的,当问题规模不大时,可以通过穷举的方法求解其最优解。但是由于组合优化问题解的数量往往是随问题的规模呈指数增长的,就使得该问题变得难于求解了,至今没有有效的求解算法。随机算法是求解组合优化问题的方法之一,其特点是在算法中引入随机因素,算法每次运行的结果不一定一样,也不能保证每次都能够求得最优解,但是在满足一定条件下,可以以概率1收敛到最优解。
本篇将介绍两个常用的随机算法——模拟退火算法和遗传算法。
本篇内容按照难易程度划分为三个等级,读者可以根据自身需要有选择地读其中的部分或者全部内容。
第一级:第4.1节到4.3节,介绍什么是组合优化问题,通过爬山法引出局部搜索算法,结合具体的例子讲解局部搜索算法求解问题的过程,并给出了一个利用局部搜索算法求解百万皇后问题的例子。分析了局部搜索算法存在的几个问题,给出了解决这问题的基本思想。
第二级:分为两部分内容——模拟退火算法和遗传算法两部分。
第4.4节通过一个制作弹簧的实验引出了物理中的金属退火现象,并详尽地分析了为什么退火过程最终会以概率1达到系统最小内能状态。为此引入了一个“怪杯子”实验,通过类比实验,形象地讲解了退火过程中系统状态随温度变化呈现的特性。对于第二级读者这部分内容可以只关注与“怪杯子”有关的内容及得到的相关结论,跳过其中详细的数学推导部分。
第4.5节通过将组合优化问题与退火过程建立对应关系,给出了模拟退火算法,通过模拟退火过程实现改进局部搜索算法,用于求解组合优化问题。
第4.7节给出了一个利用模拟退火算法求解旅行商问题的例子,对运算结果给出了详细分析。
第4.8节、第4.9节简要介绍了达尔文进化论的基本思想,通过将组合优化问题与生物进化建立对应关系,给出了遗传算法,利用生物进化过程的优胜劣汰思想求解组合优化问题。通过一个简单的求解最大值的优化问题,详细介绍了遗传算法的求解过程,最后给出了一个遗传算法的一般性框架。
第4.11节给出了利用遗传算法求解旅行商问题的例子。
第4.13节、4.14节对比了模拟退火算法和遗传算法的异同,以猴子为例对两个算法的特点进行了对比分析。最后对本篇内容做了一个全面的总结。
第三级:第4.4节对退火过程的详细分析,给出了详细的数学推导,从理论上分析了为什么退火过程最终以概率1达到内能最小状态。
第4.6节对模拟退火算法中的参数选择,包括初始温度的设置、温度下降方法、每个温度下的循环次数、算法的终止条件等,给出了详细的指导性建议。
第4.10节对遗传算法的实现问题给出了详细的介绍,包括二进制编码、整数编码,以及相应的交叉操作方法、变异操作方法等。
第4.12节讨论了遗传算法的性能评价问题,给出了一组用于评价算法性能的函数集。
这天是个周末,小明看到一个有趣的题目——旅行商问题,尝试通过编程求解该问题。
旅行商问题是这样一个问题:一个商人,要去n个城市去卖货,要求每个城市都必须去一次,并且只能去一次,最后再回到商人的出发城市,希望找到一条满足条件的最短行走路径。
小明一开始并没有觉得这个问题有多难,没有多想,打开电脑就埋头编写起了程序。小明采用的是一种比较简单的算法:穷举所有可能的走法,从中选出一条最短的路径。
很快小明就写好了程序,先从5、6个城市开始,逐渐增加到10个城市做测试,程序都很快运行出结果,经检验后结果正确。小明很高兴,一下子把城市数增加到了20个,这次出问题了,程序一直没有返回结果。小明开始以为程序可能存在错误,经反复检查后没有发现任何问题。小明看天色不早了,就想着让电脑运行一晚上,自己去睡觉休息,等第二天再看结果。第二天一早醒来,小明马上去电脑上查看运行结果,发现程序还在运行中,没有得出任何结果。
小明有些沮丧不明白这是为什么,吃完早饭后就又去找万能的艾博士,希望从艾博士那里找到答案。
第一节:组合优化问题
听了小明的疑问后,艾博士哈哈大笑起来:小明啊,你想用穷举的方法一个晚上就求出20个城市的旅行商问题吗?那是不可能的。旅行商问题是一个著名的组合优化问题,当城市数量增多时,会出现组合爆炸问题,可能的路线非常多,以至于不可能在短时间内穷举出所有可能的路线。
小明有些不解地问到:这个问题有这么复杂吗?
艾博士:我们一起来分析一下这个问题吧,分析完你就知道这个问题有多么复杂了。对于n个城市的旅行商问题,可能的路线总数共有n!个,当城市数为20时,20!等于2432902008176640000,这是个非常庞大的数字。据估算在10亿次/秒的计算机上穷举出所有可能的路线的话,大约需要77年时间。
小明惊叹到:真是没有想到,竟然需要这么长时间啊,这个问题有什么好的算法吗?
艾博士:对于组合优化问题,目前提出了一些求解算法,其中随机算法是求解组合优化问题的一类可行的算法,今天我们就讲解一下这类随机算法。
小明:什么是随机算法呢?
艾博士:随机算法就是引入了随机因素的算法,每次运行结果存在一定的随机性,但是当运行次数足够多以后,可以大概率找到一个还不错的解。
小明等不及地说:那就请艾博士给我们介绍一下随机算法吧。
艾博士:好的,我们先从组合优化问题说起。
一般的优化问题可以描述如下:
设x是决策变量,D是x的定义域,f(x)是指标函数,g(x)是约束条件。则优化问题可以表示为求解满足g(x)的f(x)最小值问题。即:
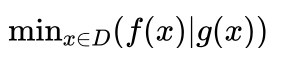
如果在定义域D上,满足约束条件g(x)的解无论有多少,但是只要总数是有限的,则优化问题称为组合优化问题。
比如旅行商问题,其约束条件就是每个城市去一次,并且只去一次,在此约束条件下,求到达所有城市并回到出发城市的最短路径。每一个可能的路线就是问题的一个解,对于n个城市的旅行商问题解的个数为n!个,虽然解的数目很多但是有限个。所以该问题属于组合优化问题。
对于组合优化问题,由于其解的个数是有限的,当问题规模比较小时,可以通过穷举的办法求解,但是当问题规模比较大时,由于解的数量实在太多,以至于无法在短时间内求解,所以就不可能用穷举的办法求解了。
小明:我采用穷举法求解该问题,难怪当5、6个城市时很快就能得到结果,而城市数达到20个时就不行了。
艾博士:有很多组合优化问题,除了旅行商问题外,常见的有背包问题、装箱问题等,我们不再多做介绍,有兴趣了解的话,可以到网上搜索,有很多的介绍。
小明:类似旅行商问题这样的组合优化问题,有什么实际意义吗?
艾博士:一些著名的组合优化问题都是真实实际应用问题的抽象化,均具有重要的实际意义和工程背景。比如旅行商问题最初就是为交通运输设计行驶路线而提出来的。比如一架飞机航线的安排,快递员给多个不同地址的客户送快递,校车的行驶路线等。这些都是旅行商问题最直接的应用,还有很多问题可以转化为旅行商问题求解。比如在制作印刷电路板时,要在上面打成百上千个孔,打孔机通过移动钻头位置实现打孔,如何设计钻头的移动线路而使得打完全部孔后移动的距离最短呢?这其实就是典型的旅行商问题。
小明:看来还真是有很多实际的应用背景。
艾博士:由于这些问题都有很强的实际应用背景,为此人们研究一些不一定能求得最优解,但往往能得到一个满意解的算法,以此来降低算法的复杂性,以便在一个可以接受的时间内得到一个还不错的解。对于实际问题,很多情况下追求最优解并不一定有意义,一个满意解就可能足够了。这就如同夏天去买西瓜。你没有必要非要买一个北京市最甜的西瓜,甚至于也没有必要买一个西瓜摊中最甜的西瓜,因为这样选择西瓜的工作量太大了。你只需从面前的3~5个西瓜中选择一个最好的就可以了。如果你对西瓜的评价是正确的话,那么这样选择出来的西瓜应该是一个令你满意的西瓜,而且与“最甜的西瓜”也不一定有多大的差别。
局部搜索算法就属于这样的一种算法。
小明:这是一个很有意思的问题。前几天同学来我家玩,我们一起讨论过最优路径的问题。从我家到同学家最短路径怎么走?经用导航软件多次测量,我们平时凭感觉走的基本就是最短路径,可能就是您说的满意解吧?因为如果非要走一条最短路径的话,会觉得比较复杂,第一步就不知道怎么迈了,因为随便迈一步出去就可能偏离了最短路径,虽然可能只是相差几厘米。
艾博士:对,就像小明说的那样,这就是满意解和最优解的区别。如果去同学家只想走一条比较近的路的话,我们可以不假思索地就出发了,虽然可能不是最短路径,但一般情况下比最短路径也长不了多少。但是如果非要求走一条最短路径,那么这个问题就复杂多了,以至于第一步都不知道迈向哪里。
小明读书笔记
给定约束条件下的最优化问题,如果解的数量有限时就是组合优化问题。对于组合优化问题,解的数量往往随问题规模呈指数增长,所以当问题规模比较小时可以通过穷举出所有解的方法求解其最优解,但是当问题规模比较大时,由于解的数量过于庞大不可能在允许的时间内穷举出所有可能存在的解,从而使得组合优化问题变得困难起来,至今还没有有效的求解算法。寻求满意解而不一定是最佳解是求解组合优化问题的路径之一。
未完待续

