第五篇 统计学习方法是如何实现分类与聚类的（十四）
清华大学计算机系 马少平
第十四节：K均值聚类算法
小明：艾博士，您介绍了几个常用的分类算法，那么有哪些聚类算法呢？
艾博士：前面我们介绍的几种方法都属于分类方法，属于有监督学习，其特点是训练集中每个样本均给出了类别的标注信息，统计学习方法根据样本的特征取值以及标注信息进行学习，然后利用学习到的分类器实现对待分类样本的分类。而聚类问题面对的是只有特征取值而无标注信息的样本，目的是按照样本的特征取值将最相近的样本聚集在一起，成为一个类别。由于聚类问题缺乏标注信息，不同的相似性评价标准会造成不同的结果。
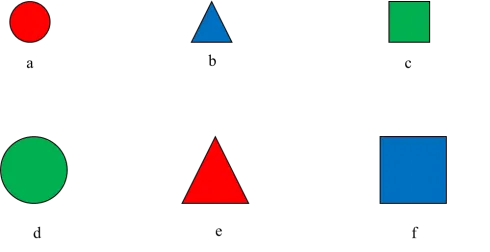
图5.48 聚类问题示意图
俗话说：物以类聚，人以群分。什么是“类”？什么是“群”？反应的是具有某种相同特征的物或者人聚集在一起，但是什么是相同特征？角度不同也可能会有不同的结果。比如图5.48所示的6个样本，如果按照形状聚类，a和d、b和e、c和f分别为一类；如果按照大小聚类，则a、b、c为一类，d、e、f为另一类；如果按照颜色聚类，则有a和e、b和f、c和d各为一类。按照哪种标注聚类都有其一定的道理。
小明：看起来聚类问题比分类问题更加复杂。
艾博士：相对来说，分类问题研究的比较充分，有很多比较成熟的算法，而聚类问题则研究的还比较欠缺，不如分类问题那么成熟，K均值算法是其中一种常用的聚类算法。
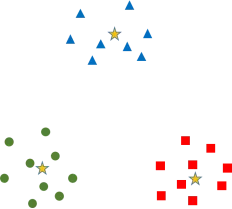
图5.49 聚类问题举例
我们看图5.49所示的红绿蓝三种颜色的样本点（暂时先忽略掉其中的三个黄色五角星“”），小明如果你看到这样的样本分布，你会把它们聚集成几个类别呢？
小明不假思索地回答说：从图中的样本分布情况看，结果是很显然的，每种颜色的样本点聚集在一起，聚集成三个类别就可以了。
艾博士：是的，我们人一看就明白，相同颜色的样本应该聚集在一起，因为这些样本彼此之间都比较密集，距离比较近，相互簇拥在一起，而与其他颜色的样本距离比较远。因此我们可以很容易想到，可以采用聚集后相同类别中样本之间的距离之和，也就是簇拥程度来评价聚类结果的性能。类内样本越是紧密地簇拥在一起，说明聚类效果越好。
如果用 ck 表示第k个类别，则类别 ck 的簇拥程度可以用类中任意两个样本间的距离平方和 Dk 做评价: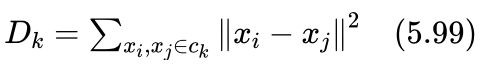
其中 xi(i=1,2,...,N) 为训练样本，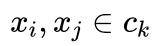 
表示被归到 ck 类的任意两个样本。
我们的目的是希望聚集后的所有类别均比较好地簇拥在一起，所以可以用所有类别的 Dk 之和J做评价指标：
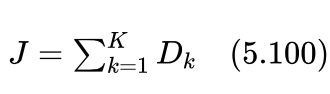
因此，按照前面的分析，J最小的结果应该是一个合理的聚类结果。
考虑到不同类别包含的样本数有多有少，为了消除因类别样本数多少带来的影响，我们除以类别中的样本数，求 Dk 的平均值 Dk' ：
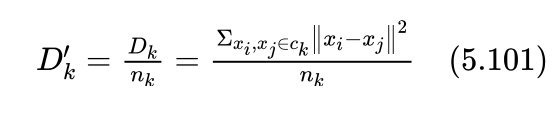
其中 nk 为第k个类别中含有的样本数。
容易证明：
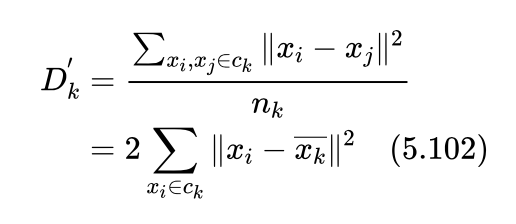
由此得知，反应类别簇拥程度的 Dk' 与类内每个样本到类别中心距离的平方和等价。
这样，我们用 Dk'重新定义J：
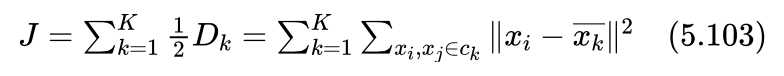
所以我们得到聚类目标就是在给定类别数K的情况下，寻找一个J最小的聚类结果。
对于N个样本数、K个类别的聚类问题，其所有可能的聚类结果数为（为了得到一个简单的表达式，我们这里假设了某个类别包含的样本数可能为0的情况）：
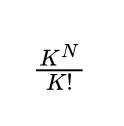
即便类别数K不大的情况下，随着样本数N的增长，所有可能的聚类结果数将很快达到天文数字。比如当K=3、N=1000时，所有可能的聚类结果数为 2.20*10^476 ，即便在当今最快的计算机上，产生出所有可能聚类结果需要的时间可能比宇宙的年龄还要长。所以不可能采用先产生出所有的聚类结果，然后从中挑选出J值最小结果的方法实现聚类。
小明：那么应该如何实现聚类呢？
艾博士：按照式(5.103)，为了使得J最小，就应该是每个训练样本到其所在类的中心距离的平方最小。如果假设我们知道了K个类别中心 的话，把每个样本归类到其距离类中心最近的类别就可以了。也就是分别计算每个样本到K个类别中心的距离，到哪个类别中心的距离最近，就将该样本归类到哪个类别中。因为任何一个样本如果不按照该原则进行归类，都会导致J值增加，所以这样得到的结果应该是J值最小。
小明：这是一个很好的归类样本的方法，但是我们并不知道K个类别中心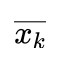 
啊，在不知道类别中心的情况下，如何实现聚类呢？
艾博士：K均值算法就是为解决该问题提出的一种聚类算法，该算法通过迭代的方法逐步确定每个类别的聚类中心。在开始的时候，先随机地从训练样本集中选择K个样本作为类别中心，然后按照距离，将样本归类到距离类别中心最近的类别中，这样每个类别就有了一些样本。将同一个类别中的所有样本累加在一起，再除以该类别中的样本数，对类别中心进行更新。然后再按照新的类别中心对样本做聚类。重复以上操作，直到所有的类别中心不再有变化为止。这就是K均值聚类算法，通过一步步迭代的方式逐步确定类别中心，并实现对样本的聚类。
下面我们举一个例子，样本分布如图5.50所示，共有6个样本，分别为：
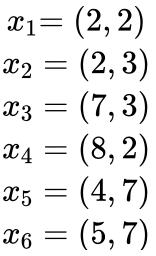
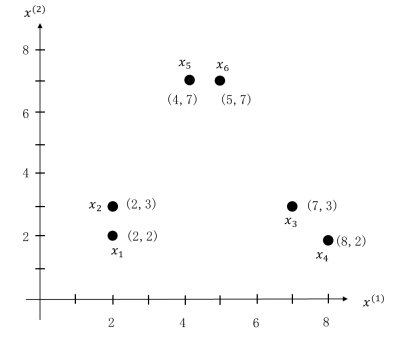
图5.50 K均值聚类举例
如何用K均值算法将这6个样本聚集成3个类别。
首先我们随机地选择3个样本作为初始的类别中心。从图中可以看出，6个样本刚好组成了3个簇团，如果选择的3个样本刚好在三个不同的簇团中的话，比如说是x1 、x3、x5 ，则以这三个样本点作为3个类别的中心，很容易就将 x1 和 x2 归类到一个类别 x3 和 x4、x5 和 x6 分别归类到另两个类别中，这也是我们希望得到的结果。
但是一般来说我们没有这么好的运气，这时就要通过迭代，一步步地逐步获得每个簇团的类别中心。比如说初选的三个样本是 x1、x2、x3 ，分别以这三个样本作为类1、类2、类3三个类别的中心，计算所有样本到三个类别的距离，结果如表5.6所示。
表5.6 样本点到类别中心的距离
由上表可以看出，样本x1 距离类1最近，样本 x2 和 x5 距离类2最近，样本 x3 、x4 、x6 距离类3最近，由此得到聚类结果：x1 在第一类、 x2 和 x5 在第二类，x3 、x4、x6 在第三类，如图5.51所示。至此我们得到了第一次聚类结果。
根据第一次聚类结果，重新计算各类别中心，由于第一类只有x1 一个样本，所以类别中心还是 x1 。第二类含有 x2 、x5 两个样本，类中心为两个样本的平均值(3,5)，图5.51中蓝色“”所示。第三类含有x3 、x4、x6 三个样本，类中心为三个样本的平均值(6.7,4)，图5.51中绿色“”所示。
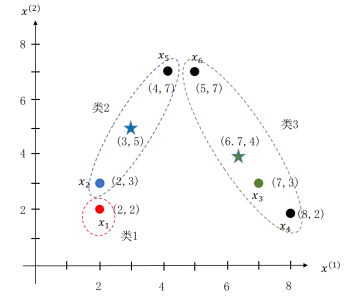
图5.51 例题的第一次聚类结果
以新的类别中心再次计算每个样本到三个类别中心的距离，如表5.7所示。
表5.7 样本点到类别中心的距离
依据上表，我们有样本 x1 和 x2 距离类1最近，被归类到类1，样本 x5 和 x6 距离类2最近，被归类到类2，样本 x3 和 x4 距离类3最近，被归类到类3。
图5.52 例题的第二次聚类结果
图5.52给出了这次的聚类结果。至此我们得到了第二次聚类结果。
再次根据新的聚类结果更新三个类别中心，得到新的类别中心分别为(2,2.5)、(4.5,7)、(7.5,2.5)，据此结果再次对样本聚类，结果如图5.53所示，其中三个不同颜色的“”代表了三个类别中心。该结果与上一次聚类结果一致，更新后的类别中心不再发生变化，K均值算法结束。得到的最终聚类结果为：类1包含样本 x1、x2 ，类2包含样本 x5、x6 ，类3包含样本x3 、x4 ，与我们预想的结果一致。
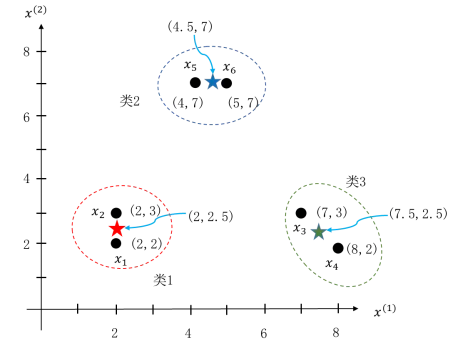
图5.53 例题的第三次聚类结果
小明：K均值聚类算法看起来并不复杂，从例题看效果也很好。但是这样得到的类别中心一定是实际的类别中心吗？
艾博士：小明提出的问题确实是K均值算法存在的一个问题，因为算法得到的类别中心与初始K个样本点的选择有关。不同的选择结果，最终得到的聚类结果可能会不一样。为此一般是做若干次聚类，从中选择一个聚类效果好，也就是J值（见式(5.103)）最小的结果作为最终的聚类结果。
小明：除此以外是否还有其他的方法呢？总觉得做若干次聚类会影响聚类效率，做几次合适似乎也不明确。
艾博士：确实是这样的，原则上来说，做的次数越多，找到最好的聚类结果的可能性也就越大，但是效率也就越低。为此也有学者提出了二分K均值聚类算法，该算法相对来说对初始类别中心的选择不是那么敏感，可以获得比较好的效果。
二分K均值聚类算法的基本思想也比较简单，先将原始样本用K均值算法聚类成两个类别，然后从聚类结果中选择一个类别，将该类别再聚类成两个类别，这样一次次“二分”下去，直到得到了K个类别为止。
小明：就是说从已有的聚类结果中，每次选择一个类别做K为2的K均值聚类，如何选择哪个已有类别做下次二分聚类呢？选择包含样本数最多的类别？或者按照式(5.99)选择Dk 最大的类别？
艾博士：也不尽然。比如图5.54所示的情况，类1是一个大类， Dk 也比较大。但是这个例子中显然将类1再二分为两个类别是不合理的，而是应该选择类2，将类2二分成两类才比较合理。由于我们总的聚类目标是使得J值最小，所以应该选择二分后能最大降低J值的类别，与聚类的总目标一致，这样才可能得到一个比较好的聚类结果。如何做到这一点呢？一种简单的办法就是对每个已有类别均做一次二分聚类，然后从中选择产生J值最大降幅的类别作为结果。
图5.54
小明：这不是又回到了穷举吗？
艾博士：一般来说类别数不是太大，而且与类别数是线性关系，所以这种情况下穷举还是可以接受的。
小明：艾博士，您在前面的介绍中，无论是K均值算法还是二分K均值算法，都假定了聚类的类别数K是已知的。那么如何确定类别数K呢？
艾博士：如何确定类别数K确实是一个重要的问题，因为类别数对聚类结果会有比较大的影响。不只是K均值算法存在这个问题，很多其他的聚类算法也存在类似的问题，或者要求给出类别数，或者虽然不直接要求类别数，但也往往是转化为其他的指标。下面我们给出一个相对比较简单的确定类别数K的方法。
因为我们希望的聚类结果是J值最小，那么就可以在给定多个不同K的情况下做聚类，观察J值的变化情况。
小明听到这里马上回应说：给定多个不同的K，选择一个J值最小的结果是不是就可以了？
艾博士：一般情况下，K越大J值就会越小，极限情况下，每个样本为一类时，J值达到最小值0，而显然一个样本一个类别不是我们想要的结果，所以不能简单地以J值最小作为选择K值的原则。
小明不好意思地说：我又把问题想简单了。
艾博士：一般来说，当逐步增加K值时，开始阶段J值会随着K值的增加下降的比较快，下降到一定程度之后，随着K值的增加J值的下降就开始变得比较缓慢了。因此，一种确定K值的办法就是先做出K值与J值的关系曲线，在曲线上找到J值下降变缓的拐点，以此处的K值作为聚类的类别数。如图5.55所示，当K从1增加到4时，J值一直下降的比较快，然后J值开始下降的比较缓慢，所以类别数为4是一个比较合适的结果。
还有一些其他确定K值的方法，我们就不详细叙述了。
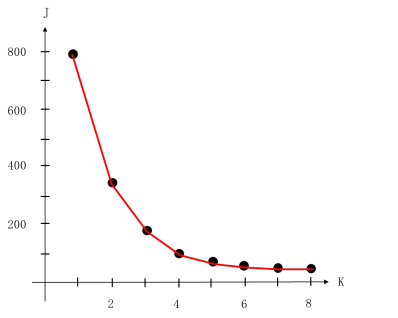
图5.55 J随K下降示意图
小明读书笔记
K均值算法是一种聚类算法，其特点是数据集中的样本不具有标签信息，根据每个样本的特征，将最相近的样本聚集在一起。
K均值算法随机地选取K个样本作为初始的类别中心，按照到哪个类别中心距离最近归类到哪个类别的方法，将所有样本归类到K个类别中。然后用每个类别中所有样本特征的平均值作为该类别的新的类别中心，再次将所有样本进行归类。反复该过程，直到所有类别中心不再发生变化为止。
K均值算法的聚类结果受初始类中心的选择影响比较大，可以通过多次聚类，从中选择一个J值最小的结果作为最终的聚类结果。
相对来说二分K均值聚类受初始类中心的选择影响比较小。其方法是刚开始所有样本为一个大类别，采用K均值算法将其聚类为两个类别。然后从已有的类别中选择一个类别，再次将该类别聚集为两个类别，直到得到了K个类别为止。每次选择使得J值下降最大的类别做二分K均值聚类。
一般来说，随着K值的增加，J值会逐渐下降。开始时J值下降的比较快，然后下降的越来越缓慢。从K—J变化图中选择一个K值，当K再增加时J值下降开始变缓了，则以该K值作为聚类的类别数。
未完待续