第五篇 统计学习方法是如何实现分类与聚类的(十五)
清华大学计算机系 马少平
第十五节:
层次聚类算法
艾博士:层次聚类算法假设数据具有一定的层次结构,按照分层聚类的方式进行聚类。
小明:什么是数据的层次结构呢?
艾博士:很多数据都有层次上的结构特性。比如在体育比赛中,100米、200米、400米都属于短跑项目,800米、1500米属于中跑项目,3000米、5000米、10000米属于长跑项目,跳高、跳远属于跳跃项目,标枪、铁饼属于投掷项目,而短跑、中跑和长跑又属于竞赛项目,跳跃、投掷属于田赛项目,径赛项目和田赛项目又同属田径项目……,如图5.56所示,第一层就是体育一个大类,第二层有球类、田径、水上项目等类别,第三层是田赛、径赛项目……,不同层次类别粒度大小不一样,越向上粒度越粗,越向下粒度越细。
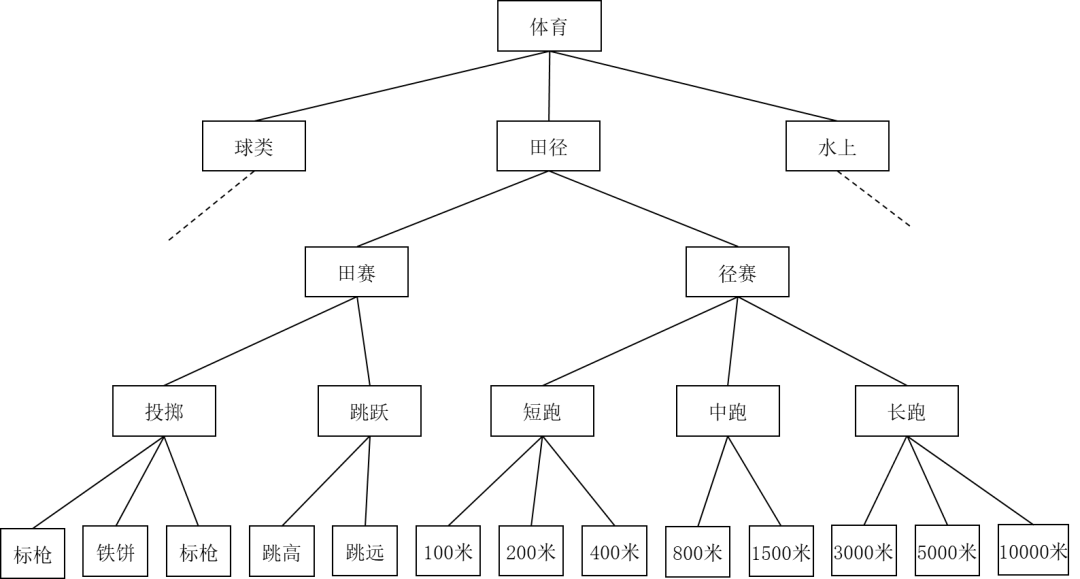
图5.56 层次聚类举例
小明:看起来层次聚类可以得到不同粒度下的聚类结果,可以根据需要选择聚类结果了。
艾博士:是这样的,层次聚类结果可以如图5.56所示那样,采用树状结构将所有聚类结果保存下来,根据需要可以自由选择不同层次的聚类结果。
层次聚类一般采取自底向上的方式进行。最开始,每个样本为一个类别,然后每次合并两个最相似的类别,逐步增加类别的粒度。如果事先规定了希望聚类的类别数K,则聚成K个类别后算法就可以停止了,或者一直到最终聚成了一个类别为止。
小明:如何判断两个类别的相似性呢?
艾博士:可以按照距离来计算相似性,距离最近的两个类别最相似,也可以采用相似度的计算方法,相似度最大的两个类别最相似。无论是距离还是相似度都有很多种不同的方法,每种方法都可以用来度量两个类别的相似性,我们不再多做介绍了。下面我们通过图5.57说明层次聚类算法的聚类过程。
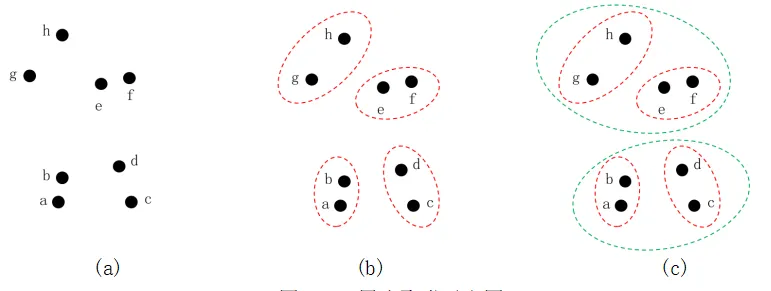
图5.57 层次聚类示意图
图5.57(a)给出的是原始8个样本,开始时每个样本为一个类别。按照距离计算任意两个样本的距离,选出距离最小的两个类别聚集为一类。假设a、b间距离最小,故将a、b合并为一类,称为ab类。按此方法依次分别得到ef类、dc类和gh类共4个类别,如图5.57(b)所示。如果我们希望的类别数为4,那么聚类到此结束,否则继续聚类。分别计算ab、ef、dc和gh四个类别相互之间的距离,选出距离最小的一对类别,假设是ab类和cd类距离最近,则将ab类和cd类合并为一个类别abcd类。如果我们希望的类别数是3,则得到了abcd类、ef类和gh类三个类别,否则继续聚类。再次计算abcd类、ef类和gh类三个类别相互之间的距离,选出距离最小的一对类别,假设是ef类和gh类,将它们合并为一个类别efgh。至此只有两个类别了,聚类结束,得到了图5.57(c)所示的聚类结果。
小明:这是一个很形象的例子,通俗易懂地给出了层次聚类的具体过程。
艾博士:前面说过,度量两个类别的相似性从距离角度、从相似性角度都有很多不同的方法,即便度量方法确定后,如何具体计算两个类的距离也有不同的方法,方法不同,也会得到不同的聚类结果。下面介绍几种常用的方法。
(1)中心距离法
以两个类别中心的距离作为两个类别之间距离的度量,其中类别中心为该类别中所有样本点的平均值。
(2)平均距离法
以两个类别中任意两个样本间距离的平均值作为两个类别之间距离的度量。注意这里的“两个样本”分别来自不同的类别。
(3)最小距离法
以两个类别中任意两个样本间距离的最小值作为两个类别之间距离的度量。同样,这里的“两个样本”分别来自不同的类别。
(4)最大距离法
与方法(3)刚好相反,以两个类别中任意两个样本间距离的最大值作为两个类别之间距离的度量。
小明:这里的前两种方法比较容易理解,后面的最小距离法和最大距离法有什么特点呢?
艾博士:不同方法得到的聚类结果是不同的,最小距离法常常会使得类别边界靠的比较近的类别连接起来,可能会得到条状的聚类结果。而最大距离法则强调同一个类别中距离最大的样本点相聚的别太远。图5.58给出了这样的例子,其中(a)是原始样本点,(b)是采用最小距离法得到的聚类结果,(c)是采用最大距离法得到的聚类结果。
小明:看来不同的距离计算方法确实可以得到不同的聚类结果,看起来也都有道理。
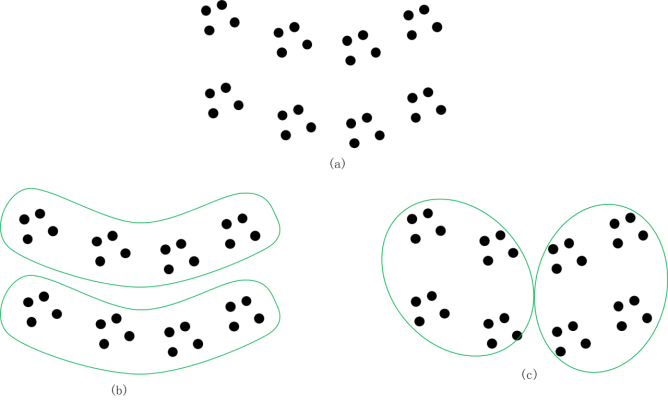
图5.58 不同方法的聚类效果示意图
小明读书笔记
分层聚类方法假定数据具有一定的层次结构,按照自底向上的方法逐步实现聚类。最开始的时候,每个样本为一个类别。每次选择两个距离最近的类别合并为一个类别,直到获得了指定的K个类别,或者只剩下两个类别为止。层次聚类可以得到一个具有层次性结构的聚类结果,可以根据需要选择不同粒度的聚类结果。
有不同的方法计算两个类别的距离,包括中心距离法、平均距离法、最小距离法和最大距离法等,不同的计算方法可能会得到不同的聚类结果。
未完待续

