第五篇 统计学习方法是如何实现分类与聚类的（十三）
清华大学计算机系 马少平
第十三节：
支持向量机用于多分类问题
小明：艾博士，前面我们讲解的支持向量机都是针对二分类问题的，也就是说只有两个类别，如何用支持向量机求解多分类问题呢？
艾博士：支持向量机也可以求解多分类问题，但不是直接求解，而是通过多个二分类支持向量机组合起来求解多分类问题。也有多种不同的组合方法，为了简单起见，下面我们以线性支持向量机为例介绍几个常用的组合方法，也同样适用于非线性支持向量机。
（1）一对一法
设共有K个类别，则任意两个类别建立一个支持向量机，对于一个待识别样本x，送入到每个支持向量机中做分类。这样每个支持向量机都会有一个结果，该结果可以看做是对x所属类别的一次投票，哪个类别获得的票数最多，x就属于哪个类别。比如说想识别猫、狗、兔三种动物，则分别用猫和狗、猫和兔、狗和兔建立三个支持向量机，对于一个待分类的动物样本x，分别送到这三个支持向量机中做分类。假定第一个支持向量机输出为猫、第二个支持向量机也输出为猫、第三个支持向量机输出为兔，则猫获得2票、兔获得1票、狗获得0票，根据投票结果，猫获得的票数最多，则x被分类为猫。
小明：如果K个类别中任意两个类别都要建立支持向量机，当K比较大时岂不是要建立很多个支持向量机？
艾博士：一对一法的优点是识别性能比较好，分类准确率高，但不足就是需要的支持向量机比较多，当类别数为K时，需要建立 K(K-1)/2 个支持向量机，约等于 K^2/2 个。比如对于0～9数字识别问题，类别数K为10，需要建立的支持向量机数量为10*(10-1)/2=45个，当类别数为100时，需要建立的支持向量机数量约为5000个，而当类别数为1000时，需要建立的支持向量机数量则要达到约500000个。
图5.42给出了一对一法做三分类时的示意图。图中绿、红、蓝三种颜色分别代表类1、类2和类3，任意两类之间共建立了3个支持向量机，其最优分界线分别为d12 、d13 和 d23。
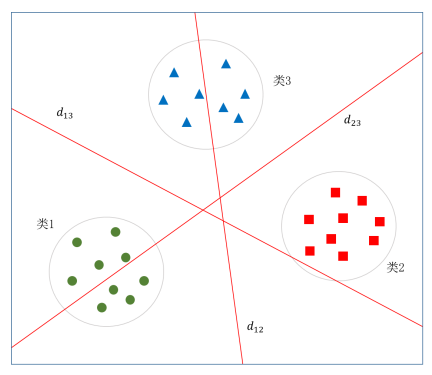
图5.42 一对一法三分类方法示意图
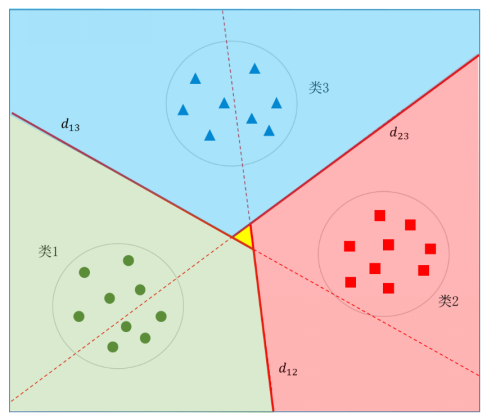
图5.43 三个类别最优决策边界示意图
图5.43给出了三个类别最优决策边界示意图，其中浅绿色区域为类1、浅红色区域为类2、浅蓝色区域为类3，待识别样本落入了哪个区域，就被分类为哪个类别。图中央的黄色三角区域为“三不管地带”，因为落入这个区域的样本每个类别都会获得一票，从而导致不能分类。这时可以去掉决策函数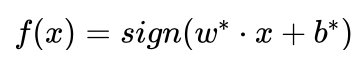 
中的符号函数sign，以 
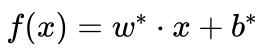作为带符号的函数间隔，按照待识别样本x到三个支持向量机最优分界线的带符号函数间隔判别其所属类别，距离哪个分界面的带符号函数间隔越大，就分类到哪个类别。
（2）一对多法
对于具有K个类别的分类问题，一对多法就是分别用每个类别做正类，其余K-1个类别合并在一起做负类，共构建K个支持向量机。还是以识别猫、狗、兔三种动物为例，需要分别以“猫为正类、狗和兔为负类”、“狗为正类、猫和兔子为负类”、“兔为正类、猫和狗为负类”构建三个支持向量机。
图5.44给出了一个具有三个类别情况下的示意图，其中直线 d1-22 表示“类1为正类、类23为负类”构建的支持向量机的最优分界线，其中“类23”表示类2、类3两个类别合并后的类别。直线 d2-13、d3-12 的含义也是同样的含义，不再多述。
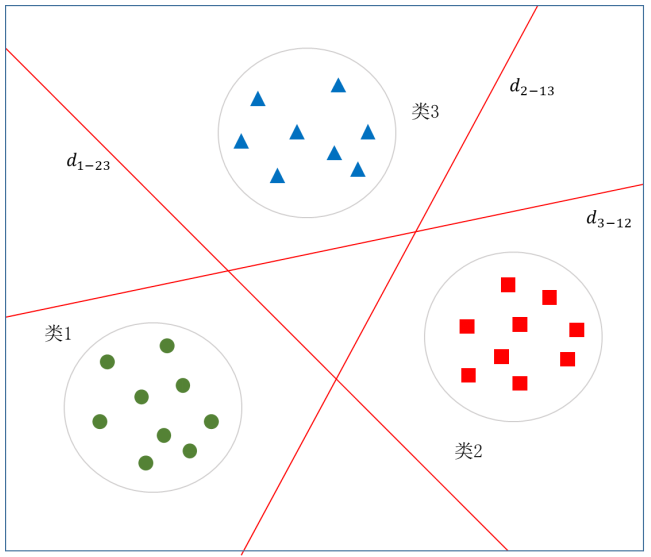
图5.44 一对多法三分类方法示意图
小明：这种情况如何用于分类呢？感觉不能采用投票法了，因为在K个支持向量机中，每个分类结果只有一个正类，而且K个结果没有重复，每个类别最多会得到一票，并且会有多个类别得到一票。
艾博士：小明分析得是对的，对于一对多法不能采用投票法做决策。像在一对一法中处理“三不管地带”一样，去掉决策函数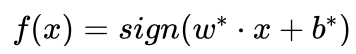 
中的符号函数sign，以 
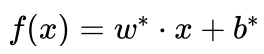作为带符号的函数间隔，按照待识别样本到三个支持向量机最优分界线的带符号函数间隔判别其所属类别，距离哪个分界面的带符号函数间隔越大，就分类到哪个类别。图5.45中给出了x、y、z三个待识别样本，图中用双箭头分别标出了三个样本到三个最优分界线的带符号函数间隔，其中红色表示正的函数间隔，蓝色表示负的函数间隔。对于样本x，只有到分界线 d3-12 的带符号函数间隔是正的，到另两个分界线的带符号函数间隔均是负的，所以自然被分类为类别3。对于样本y，到分界线 d1-23 和 d2-13 的带符号函数间隔是正的，到 d3-12 的带符号函数间隔是负的，所以类别可能是类1或者类2，由于到 d1-23 的带符号函数间隔更大，所以分类结果为类1。样本z比较特殊，到三个最优分界线的带符号函数间隔都是负的，但是由于到 d2-13 的带符号函数间隔最大（绝对值最小），所以分类结果为类2。
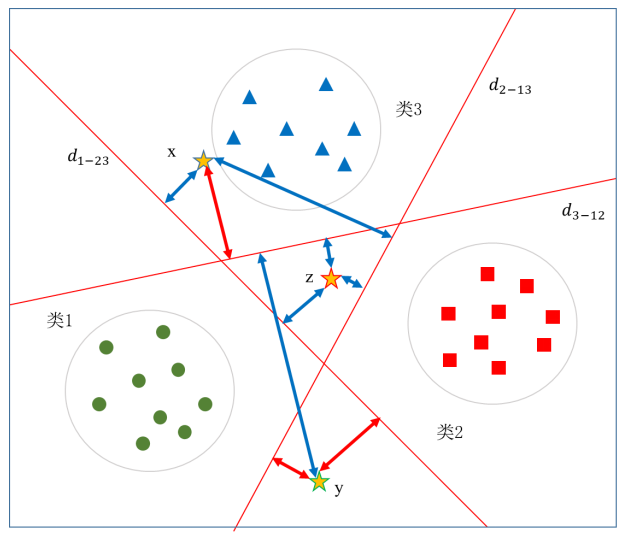
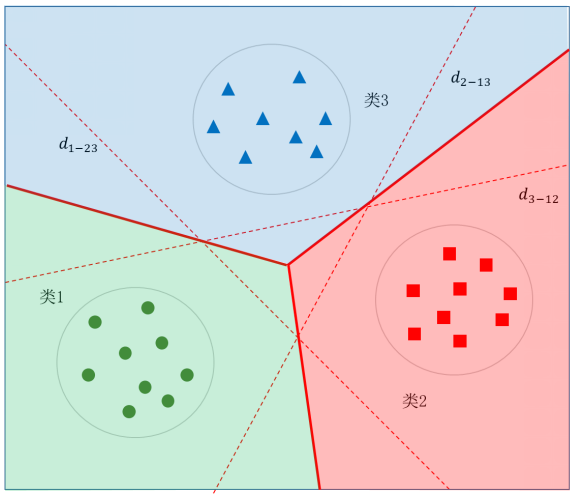
图5.45 三个待识别样本到三条分界线的函数间隔示意图
图5.46给出了三个类别最优决策边界示意图，其中浅绿色区域为类1、浅红色区域为类2、浅蓝色区域为类3，待识别样本落入了哪个区域，就被分类为哪个类别。
一对多法的特点是支持向量机数量比较少，效果也不错。不足是需要处理样本不均衡问题。因为正类只有一个类别，而负类有K-1个类别，在训练支持向量机时往往负类样本数量远多于正类样本数量。这样得到的支持向量机一般会偏向于负类，影响分类效果。一种解决办法是在求解支持向量机过程中，对正负两类样本设置不同的参数C，对于正类样本对应的 αi 用 αi+ 表示，对于负类样本对应的 αi 用αi- 表示，则限制条件中要求满足：
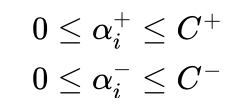
取一个比较大的 值可以一定程度上缓解训练样本不均衡所带来的问题。
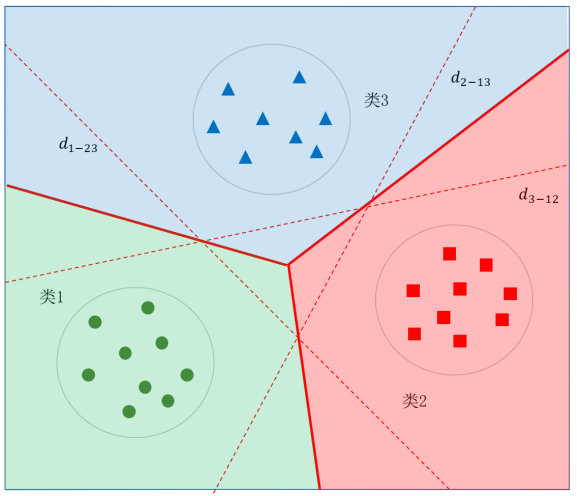
图5.46 三个类别最优决策边界示意图
（3）层次法
对于K个类别的分类问题，先将其合并成两大类构建支持向量机，然后再将每个类别分别合并成两类构建支持向量机，以此类推，直到最后能区分出每个类别。对于待分类样本，按次序输入到每个支持向量机做分类，由前一次分类结果决定下一步采用哪个支持向量机，直到最后得到分类结果。这种方法有点像一棵二叉决策树，从根节点开始用支持向量机决策所选择的子节点。图5.47给出了用层次法求解4分类问题的示意图。层次法的最大特点就是构建的支持向量机数量少，不足是会造成错误的传递，一旦前面的支持向量机出现分类错误，由于后面的分类是以此为基础的，所以只能是“将错就错”，没有任何补救的机会。
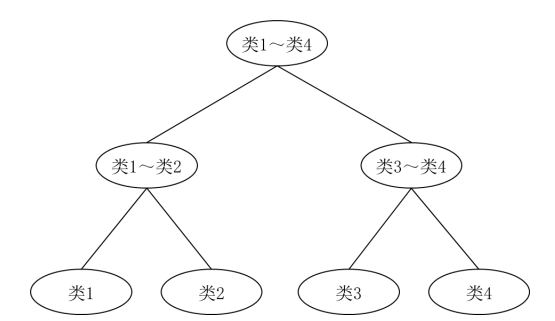
图5.47 层次法求解4分类问题示意图
小明：如果类别数是奇数时怎么划分为两个类别呢？
艾博士：类别数为奇数时也是一样的，比如有5个类别，则可以按照其中两个类别合并为一类，另三个类别合并为另一类就可以了。
小明读书笔记
支持向量机是一种二分类方法，通过求解最优分界面实现分类。
1、 对于线性可分支持向量机问题，要求训练集中每个样本到最优分界面的函数间隔大于等于1，对应如下的最优化问题：
分类决策函数为：
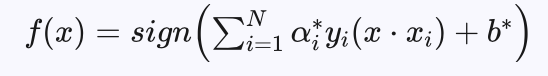
每个不为0的 αj* 对应的 xj 均为支持向量，支持向量到分界超平面的函数间隔为1，其他样本到分界超平面的函数间隔大于1。
2、对于线性支持向量机问题，允许训练集中少数样本到分解超平面的函数间隔小于1，但是要求大于等于 1-ξi ，希望ξi 尽可能地小。所以线性支持向量机对应如下的优化问题：
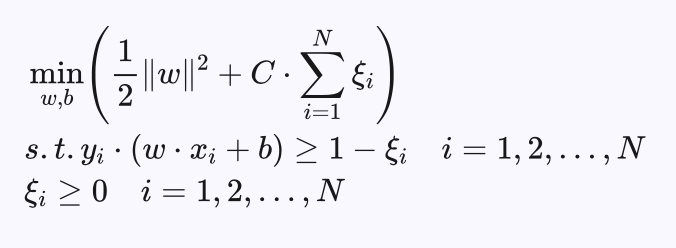
同样可以通过如下的对偶问题求解：
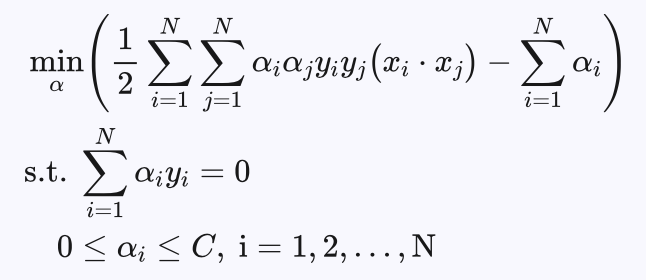
与前面线性可分支持向量机的唯一区别就是对 αi 的限制不同，线性可分支持向量机是当C趋于无穷时线性支持向量机的特例。
设最优解为：
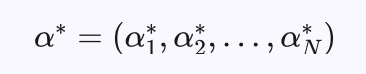
最优分界超平面方程为：
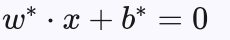
其中：
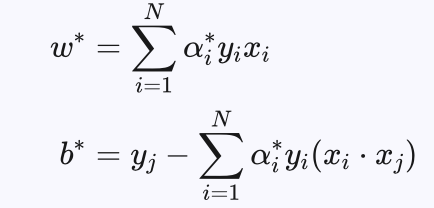
xj 、yj 是任意一个不等于0也不等于C的 αj* 对应的样本及其标注。
带入 ω* 得到超平面方程：
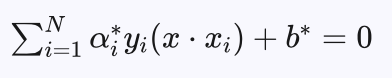
分类决策函数为：
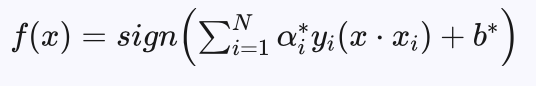
每个不为0的 αj* 对应的xj 均为支持向量，对于 0<αj*<C 对应的支持向量到分界超平面的函数间隔为1，对于 αj*=C 对应的支持向量，到分界超平面的函数间隔大于等于 1-ξi ，当 ξi<1 时，对应的样本分类正确，当 ξi>1 时，对应的样本分类错误，其他样本到分界超平面的函数间隔大于1。
3、非线性支持向量机通过一个变换，将在原空间不能线性可分的数据，映射到新的空间中，在新空间中构造支持向量机。核函数提供了一种在原空间计算新空间向量点积的方法，这样就可以在不知道变换函数的情况下，直接在原空间求解新空间中最优超平面。新空间的超平面对应原空间的一个超曲面。
非线性支持向量机问题对应的就是用核函数表示的如下的最优化问题：
4、常用的核函数包括：
5、组合多个二分类支持向量机可以构建多分类支持向量机。主要的方法有：
（1）一对一法。任意两个类构建一个支持向量机，通过投票法，得票最多的类为分类结果。
（2）一对多法。对于k分类问题，选择其中一类为正类、其余k-1类为负类，构建k个支持向量机，计算待分类样本到每个支持向量机最优分界曲面的带符号函数间隔，取其中带符号函数间隔最大的类别为分类结果。
（3）层次法。通过将训练样本逐步分成两类的方式构建具有二叉树结构的多个支持向量机，一步一步自顶向下完成分类。
未完待续