第五篇 统计学习方法是如何实现分类与聚类的（八）
清华大学计算机系 马少平
第八节：什么是支持向量机
艾博士：小明，请看图5.24所示的例子，“○”是一个类别，“△”是一个类别，如果用一条直线将两类分开，你觉得怎么分好？
小明思考了一会儿说：我觉得如图5.25所示，将红线作为两个类别的分界线比较好。
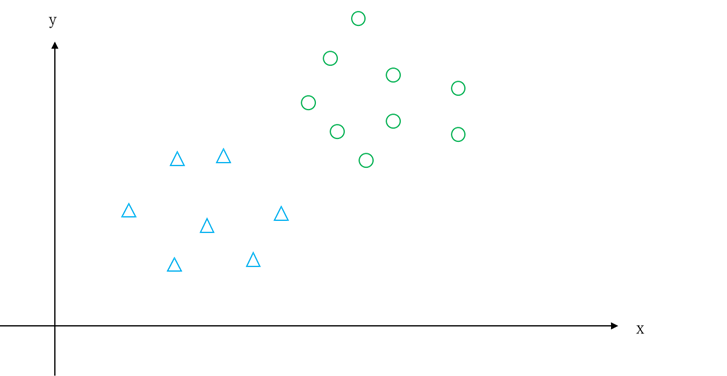
图5.24 两类示意图
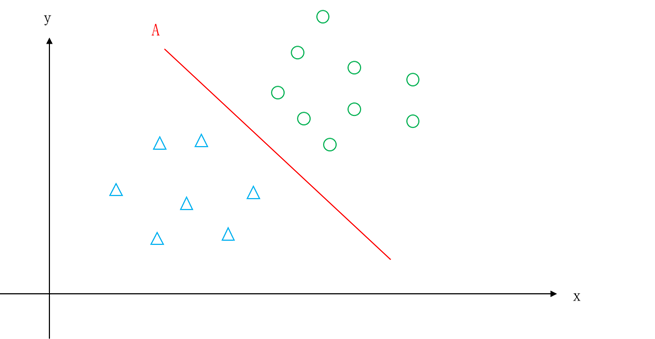
图5.25 两类示意图——一种划分方法
艾博士又接着问小明：如图5.26所示，A、B、C、D等多条直线都可以作为这个问题的分界线，你为什么选择红线A呢？
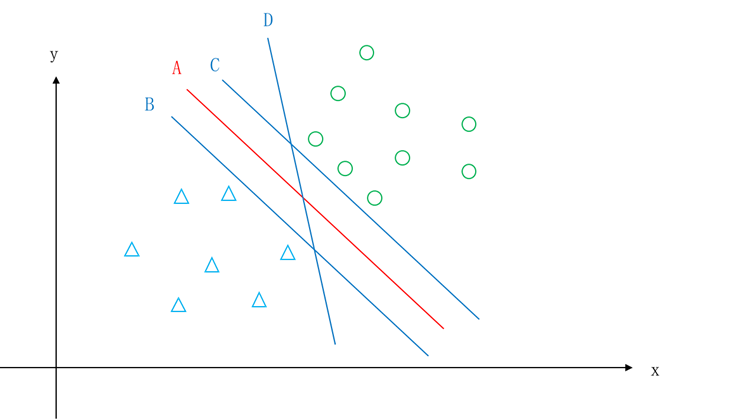
图5.26 两类示意图——多个划分方法比较
小明：从直觉上看，在两类靠近中间的地方画一条线将两类分开是比较合理的，这样对于一个待分类样本，看它在红线的哪一边，在哪边就将其分类为哪个类别。如果是按照直线B或者C作为分界线，就太靠近其中的一个类别了，而直线D则是两个类别都很靠近，也不是一个好的分界线。因为这几个分界线都不利于将来用于分类。
艾博士：小明的直觉是对的，在A、B、C、D这几个分界线中，直线A确实是最好的分界线。那么应该如何定义最优分界线呢？我们可以从小明刚才提到的“中间线”着手给出最优分界线的定义。所谓“中间线”就是不偏不倚，距离两个类别的距离是一样的。
小明：每个类别都有多个样本，如何定义直线到类别的距离呢？
艾博士：你刚才画“中间线”时是怎么考虑的呢？
小明：其实并没有想那么多，只考虑了每个类别距离直线最近的几个样本点，完全忽略了其他的样本点。
艾博士：对，直线到类别的距离就是指该类别中距离直线最短的样本的距离，而“中间线”就是到两个类别的距离相等。但是“中间线”是否就是最优分界线呢？我们看图5.27所示的情况。
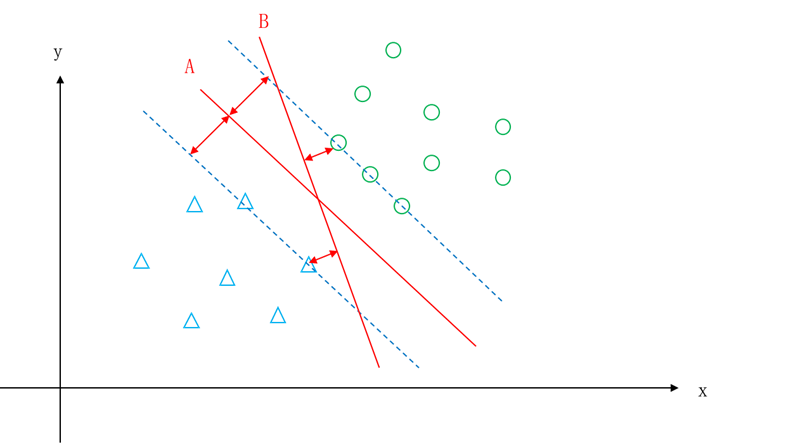
图5.27 不同的“中间线”
艾博士指着图5.27对小明说：你看图中A、B两条直线，距离两个类别的距离都是相等的，都属于“中间线”，但是哪个作为两个类别的分界线更好呢？
小明不加思索地回答说：肯定是直线A更好啊，因为A到两个类别的距离更远，更适合用于分类。
艾博士：小明说得有道理，如果分界线只是“中间线”还不够，还希望是距离两个类别的距离最远的“中间线”。综合这两点我们可以给出最优分界线的定义：
距离两个类别的距离最大的中间线，就是两个类别的最优分界线。而中间线指的是距离两个类别的距离相等的直线。
小明：明白了，如图5.27所示，直线A、B都是两个类别的中间线，但是直线A距离两个类别的距离更大，所以相比直线B，直线A更可能是最优分界线。
艾博士：上述定义通过中间线定义了最优分界线，这个定义更容易理解。事实上最优分界线可以定义的更简单：
最优分界线是使得距离两个类别的距离中最小的距离最大的分界线。
这个定义中虽然没有提到中间线，但是隐含了中间线信息，因为使得到两个类别的距离中最小的距离最大，就限制了这个分界线一定是中间线。
小明摸着头说：我还是不太明白为什么这样的直线一定是中间线。
艾博士解释说：你可以设想一下，如果不是中间线的话，是不是就会造成距离一个类别近了？比如图5.28所示，红色虚线是中间线，绿色线偏离了中间线后，距离“△”类更近了，就不满足到两个类别的距离中最小的距离最大这个条件了，这个条件一定会使得分界线处于中间线位置。
小明：我明白了，因为只有中间线才有可能满足到两个类别的距离中最小的距离最大这个条件，而距离两个类别的距离最大的中间线，就是我们希望得到的最优分界线。
艾博士：图5.29中红色直线所示的就是最优分界线。由图可以看出，最优分界线只由两个类别边缘上的a、b、c、d、e几个样本点决定，其他样本点都属于“打酱油”的，可有可无。由于欧氏空间中的一个点也可以看做是一个向量，因此a、b、c、d、e这5个样本点被称作支持向量，这5个支持向量决定了最优分界线。有了最优分界线之后，就可以用最优分界线对待分类样本做分类了。对于任意一个待分类样本，只要看该样本处于最优分界线的哪一边就可以判断其所属的类别。采用这种方法进行分类的方法称作支持向量机，简写为SVM。
小明：原来支持向量机名称是这么来的。
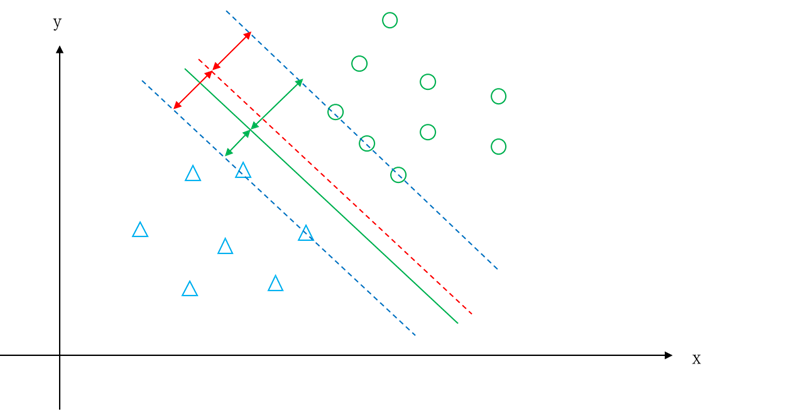
图5.28 偏离中间线的分界线
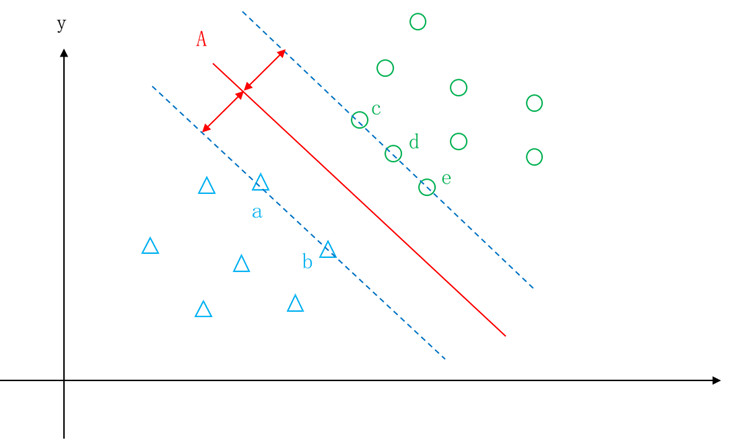
图5.29 最优分界线示意图
艾博士：这里我们一直以平面上的点，也就是样本只有两个特征取值为例进行说明，实际上特征可能是多个的，拥有成百上千个特征都是有可能的，这样的样本属于多维欧氏空间中的一个点。在多维的情况下，就不能用直线作为两个类别的分界线了，只能用超平面做分界，最优分界线就变成了最优分界面。这个最优分界面我们称作分类超平面。
小明：我们一直在介绍两个类别的情况，支持向量机如何实现多分类呢？
艾博士：原则上来说，支持向量机只能实现二分类，不能直接实现多分类，但是我们后面会讲到，任意一个二分类方法都可以经过一定的组合实现多分类问题。这一点我们留待后面再做介绍，这里先只考虑二分类问题。
小明：那么如何求解这个最优分界面呢？
艾博士：支持向量机就是要求出这个最优分界面。为了方便介绍，下面我们先介绍几个术语和概念。
设有训练集T，是N个训练样本的集合：
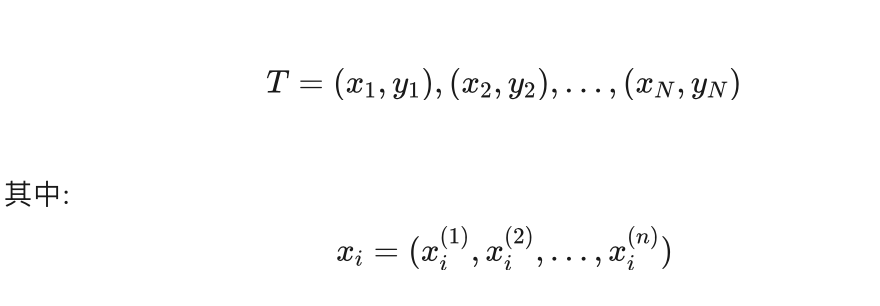
是第i个训练样本的n个特征取值组成的n维向量，对应n维欧氏空间中的一个点，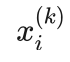 
是其第k个特征的取值。yi 是 xi 的类别，取值为1或者-1，表示正类或者负类。
假设男性类别为1，女性类别为-1，一个发长为10、鞋跟高度为5的女性样本可以表示为：
((10,5),-1)
一个发长为2、鞋跟高度为1的男性样本可以表示为：
((2,1),1)
小明问到：这里的类别yi只能表示为1或者-1吗？
艾博士：由于支持向量机求解的是二分类问题，只有两个类别，用1或者-1表示其类别，是为了方便后面的求解。所以一定要记住这里的类别标识yi只能是1或者-1，在后面的推导中我们用到了这一点。
小明：明白了，我一定记住这一点。
艾博士：最优分界面可以用平面方程表示如下：
带“*”号表示的是最优分界面，如果不带“*”号就是一个一般的超平面。一个超平面由w和b唯一决定，为了方便叙述我们用(w,b)表示一个超平面。
小明：如果知道了最优分界面方程，如何判断一个待分类样本在最优分界面的哪一边呢？
艾博士：对于最优分界面上的点，带入式(5.25)左边其结果刚好等于0，而对于不在最优分界面上的点，带入式(5.25)左边其结果或者大于0，或者小于0。大于0的点在最优分界面的一边，小于0的点在最优分界面的另一边，通过判断大于0还是小于0，就可以知道待分类样本输入哪个类别了，大于0的为1类，小于0的为-1类。
我们可以再引入一个符号函数sign，该函数当输入大于0时输出为1，小于0时输出为-1。这样对于一个待分类样本，带入到式(5.25)的左边，然后再通过符号函数sign就可以直接得到待分类样本的类别为1或者-1了。我们将函数：
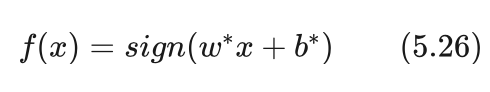
称作决策函数，对于任意一个待分类样本x，函数f(x)的输出就是x的分类结果。
所以支持向量机就是依据决策函数f(x)进行分类的方法。
下面我们举一个例子。假设2维欧氏空间中的一个最优分界线方程如下：
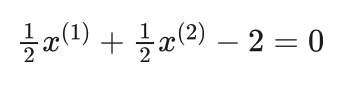
判别待分类样本 x1=(3,4) 和 x2=(-2,2) 所属的类别。小明请你计算一下这两个样本所属的类别。
小明：这个不难，将两个样本分别带入到决策函数中就可以了。
根据最优分界线方程，我们有决策函数：
艾博士：从上面这个例子可以看出，不同的样本点 带入到超平面方程(w,b)中，具有不同的取值，根据点相对于超平面的不同位置，有的大于0，有的小于0，其绝对值的大小反应了该点到超平面的距离。该距离我们称作点xi到超平面(w,b)的函数间隔。
当 xi 属于正类时，其对应标记 yi 等于1，而当 xi 属于负类时，其对应的标记 yi 等于-1，所以点xi 到超平面(w,b)的函数间隔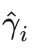 
我们可以表示为：
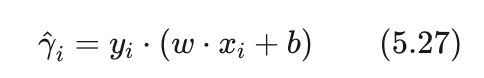
小明：这种表示挺巧妙的，乘以yi后刚好相当于是求绝对值。
艾博士：对于一个超平面(w,b)来说，w和b同时乘以一个非零的常数c，该超平面是不变的，也就是说超平面(w,b)和超平面(cw,cb)是同一个超平面，但是xi到(w,b)的函数间隔和到(cw,cb)的函数间隔显然是不一样的，因为xi 到(cw,cb)的函数间隔：
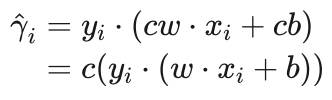
是xi 到(w,b)函数间隔的c倍。
小明：只是因为超平面的不同表示，点 xi 到同一个超平面的函数间隔竟然不同，这是不是不太合理啊？
艾博士：确实不合理。但是后面我们也会利用函数间隔的这个特点简化表示，这一点留待后面再讲。
为了解决函数间隔的不合理问题，我们可以对超平面方程做个归一化处理，即将超平面方程(w,b)除以w的范数‖w‖后再计算函数间隔，其中范数：
对于几何间隔来说，就不会由于同一个超平面的不同表示导致其几何间隔的大小不同了。因为对于超平面(cw,cb)来说：
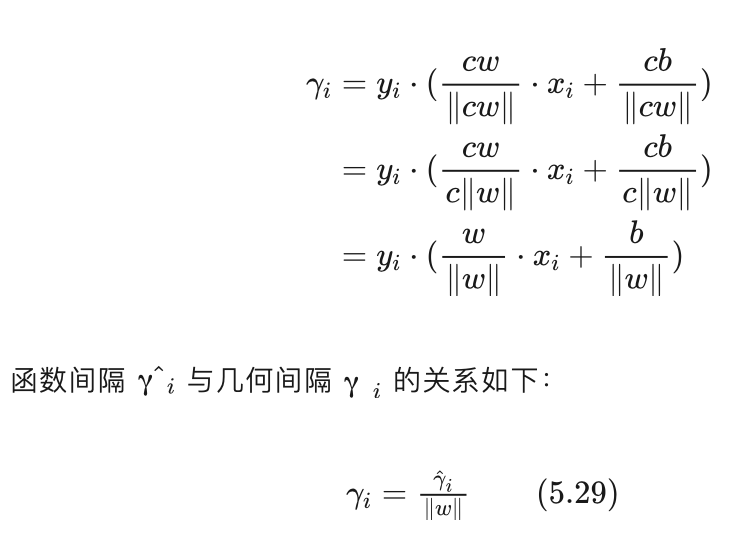
事实上，几何间隔就是我们平时所说的点到超平面的距离，一个点到一个超平面的距离不会因为超平面的不同表示而导致不同。
我们定义训练集T中样本到超平面最小的间隔为训练集T到超平面(w,b)的间隔。这样训练集T到超平面(w.b)的函数间隔为：
根据训练集T中样本分布的不同，可以构建线性可分支持向量机、线性支持向量机和非线性支持向量机，下面我们分别讨论一下这三种不同的支持向量机。
未完待续