第五篇 统计学习方法是如何实现分类与聚类的(七)
清华大学计算机系 马少平
第七节:K近邻方法
艾博士:俗话说,物以类聚人以群分,如果两个事物距离很接近,那么我们就有理由认为这两个事物很可能是同一个类别。这样,对于一个待分类样本,可以计算其与训练数据集中所有样本的距离,与其最近的一个样本的类别就可以认为是该待分类样本的类别。这种方法称作最近邻方法。
比如男女性别分类问题,我们假定有发长和鞋跟高度两个特征,取值为发长和鞋跟高度的实际值,这样[发长,鞋跟高度]就可以构成平面空间的一个点,如图5.21所示。其中“△”为训练集中男性样本的坐标,“○”为女性样本的坐标,x和y为两个待分类样本。从图中可以看出x距离样本a的距离比较近,而y距离样本b的距离比较近,而样本a、b分别为男性和女性,所以有理由认为x的类别为男性,y的类别为女性。
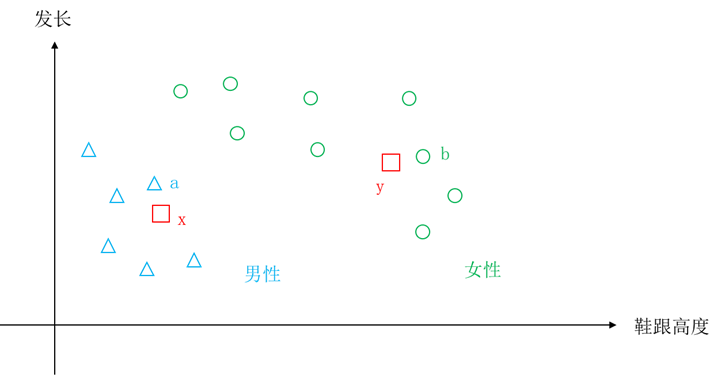
图5.21 最近邻方法示意图
小明:就是根据距离最近样本的类别作为待分类样本的距离,感觉这种方法既简单又有道理。
艾博士:但是这种方法也有一定的风险,因为数据集大了以后不可避免地会存在噪声或者标识错误,如果样本a被错误地标识成女性,那么x就会被识别成女性了。
小明:确实存在这样的问题,如果a的类别错误标识,则在其附近的待分类样本都会被识别为女性,造成识别错误。
艾博士:一种解决办法就是不仅仅看与待分类样本距离最近的一个样本的类别,而是看距离它最近的k个样本的类别,k个样本中类别不一定完全一样,哪种类别多就认定该待分类样本是哪个类别。这种方法称作k近邻方法,简称为kNN。
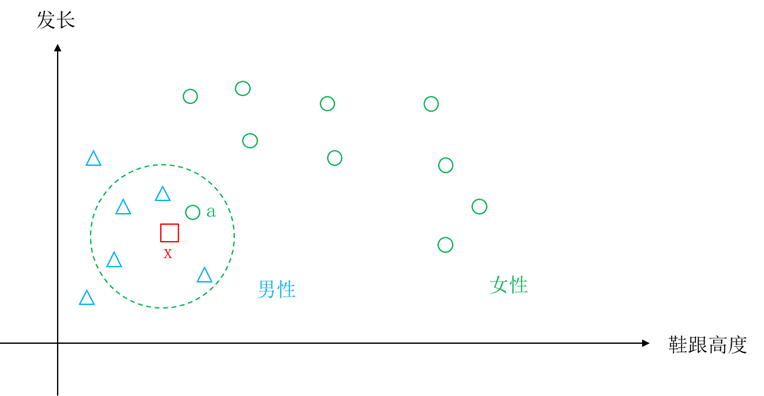
图5.22 k近邻方法示意图
图5.22给出了k近邻方法的示意图。图中距离待分类样本x最近的有5个样本,虽然样本a的类别为女性,但是其余4个样本的类别为男性,所以样本x还是被识别为男性。这就消除了因个别噪声引起的识别错误。
小明:这是一个好办法。如果是多个类别如何处理呢?
艾博士:多类别时也一样处理,就是k近邻中哪个类别的样本最多待分类样本就识别为哪个类别,不要求一定过半数。
小明:了解了。如果将k个近邻中的样本类别看成是对待分类样本类别的投票,得票最多的类别就是待分类样本的类别。但是k取多大为好呢?是不是k越大越好?
艾博士:不是的。当k为1时,k近邻方法就是最近邻方法,受噪声影响比较大,类似于过拟合,但是如果k太大时,容易造成欠拟合,极限情况下k与训练数据集的大小一致时,任何待分类样本都会被固定地识别为数据集中样本数最多的类别。所以如何选取k是k近邻方法中主要问题之一。
图5.23给出了k取不同取值时对识别结果影响的示意图。
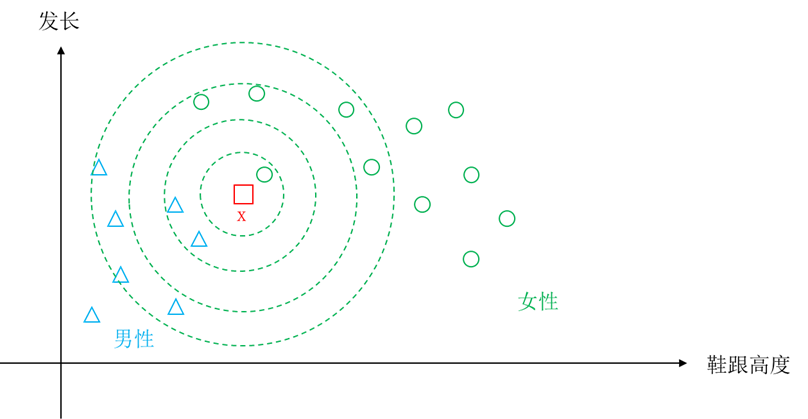
图5.23 不同k值时对结果的影响示意图
从图中可以看出,k为1时,x被识别为女性,而k为3时,3个近邻中有2个男性,x被识别为男性,k为5时,5个近邻中有3个女性,x又再次被识别为女性,k扩大为11时,11个近邻中有6个男性,x又是被识别为男性。可见k的不同取值对识别结果的影响。多大的k值合适,需要根据具体问题的样本情况,通过实验决定,选取一个错误率最小的k值。
小明:看起来k近邻方法不需要训练?
艾博士:k近邻方法直接将待分类样本与训练数据集中的每个样本计算距离,所以是不需要训练过程的,直接存储训练数据集就可以了。
小明:在k近邻方法中主要就是距离计算,这里的距离就是欧氏距离吗?
艾博士:欧氏距离是比较常用的距离计算方法,但是在k近邻方法中并不限于只是使用欧氏距离,任何一种距离计算方法都可以用在k近邻方法中。下面我们介绍几种常用的距离计算方法,在介绍中我们假定每个样本共有n个特征,样本 xi 的n个特征取值为 (xi1,xi2....,xin) 。
(1)欧氏距离
这是最常用的距离计算方法,我们平时说的两点间的距离一般是指欧氏距离。样本 xi 和样本 xj 的欧氏距离为两个样本对应特征值之差的平方和再开方。即:
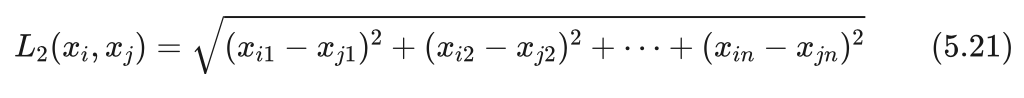
(2)曼哈顿距离
曼哈顿距离是样本xi 和样本 xj 对应特征值之差的绝对值之和,即:
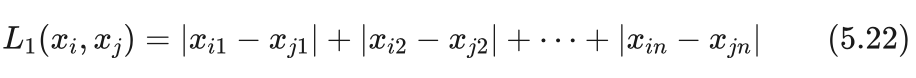
该距离又称作是城区距离,表示的是一个只有横平竖直道路的城区中,任意两点间的距离。
(3)加权欧氏距离
加权欧氏距离顾名思义就是在计算距离时,每个平方项具有不同的权重 αk ,即:
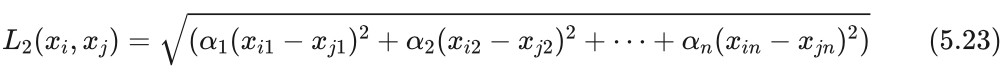
小明:如何给定权重呢?
艾博士:对于 ακ 可以从两个方面考虑,一是重要的特征其对应的权重就大,在实际应用中根据情况人为给定权重值。二是从特征取值的差异性角度考虑,比如在男女性别分类中,有发长和鞋跟高度两个特征,如果单位都是厘米,那么鞋跟高度取值区间大概在0到10厘米之间,而发长取值区间大概在0到100之间。显然取值区间大的特征其差的平方比较大,取值区间小的特征其差的平方也小,当二者差距比较大时,很有可能距离值基本由取值区间大的特征决定,而淹没了取值区间小的特征的作用。为此我们可以对取值区间大的特征赋予一个相对比较小的权重,而取值区间小的特征赋予一个相对比较大的权重。一种方法就是计算每个特征k取值的方差 Sk ,用方差 Sk 的倒数作为权重。即:
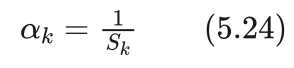
这种采用方差的倒数作为权重的加权欧氏距离又称作标准欧氏距离,是采用方差归一化的欧氏距离,消除了特征取值区间不同造成的影响。
还有一些其他的距离计算方法,我们不再多说。另外一些相似性评价方法也可以用于k近邻中,用相似性取代距离,取k个最相似的样本就可以了。
下面我们给出一个采用k近邻方法进行分类的例子。
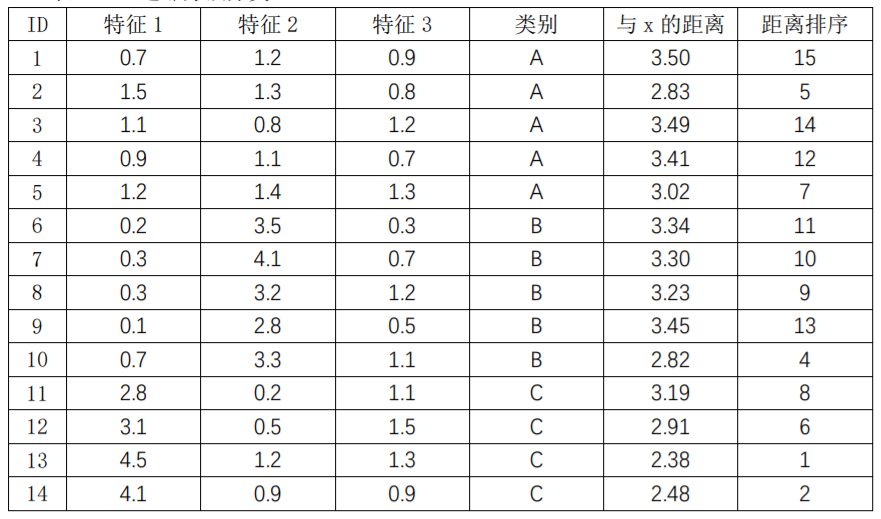
表5.5前5列给出了具有15个样本的数据集,其中第1列是样本ID,第2到第4列给出了每个样本的三个特征取值,第5列是每个样本的所属类别。第6列给出了每个样本与待分类样本x=(3.5,3.3,0.8)的距离,第6列给出了按照距离排序后的序号。从表中可以看出,当k取值为5时,与x最近的5个样本ID分别为13、14、15、10、2,其中ID为13、14、15的三个样本类别为C,ID为10的样本类别为B,ID为2的样本类别为A。按照k近邻方法待分类样本x被识别为类别C。
表5.5 k近邻方法分类

小明读书笔记
k近邻方法是一种不需训练的分类方法,按照待分类样本周围k个已知样本情况做分类,k个样本中哪个类别的样本最多就将待分类样本归到哪一类。
k近邻方法最重要的是超参数k,k过小容易造成过拟合,而k过大容易造成欠拟合,可以通过实验的办法找到一个合适的k值。
未完待续

