第三篇 计算机是如何找到最优路径的（七）
清华大学计算机系 马少平
第七节：动态规划与Viterbi算法
艾博士：动态规划是求解决策过程最优化的一种方法，Viterbi算法是其中一种常用的算法，是针对篱笆型有向图最短路径问题而提出的一种有效方法。从理论上来说，Viterbi算法与h=0时的A*算法是等价的，但是对于一类特殊问题，具有比较高的求解效率，具有非常广泛的应用。
小明：什么是篱笆型有向图最短路径问题？
艾博士：图3.31所示的就是一个篱笆型有向图最短路径问题示意图。该图由 s0、s1、...、sn+1 共n+2列组成，每列包含有数目不等的节点， wij 表示第i列的第j个节点，第i-1列第j个节点到第i列第k个节点的代价用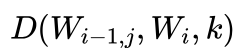 
表示。要求从每一列中选择一个节点构成从 w0 到wn+1 的路径，并使得该路径的总代价最小。这就是篱笆型有向图最短路径问题，其名称来源于图中节点是一列列组成的，像一个篱笆一样，而左右两个“篱笆”间的两个节点是从左到右有向连接的。
小明：这个名称倒是比较形象。
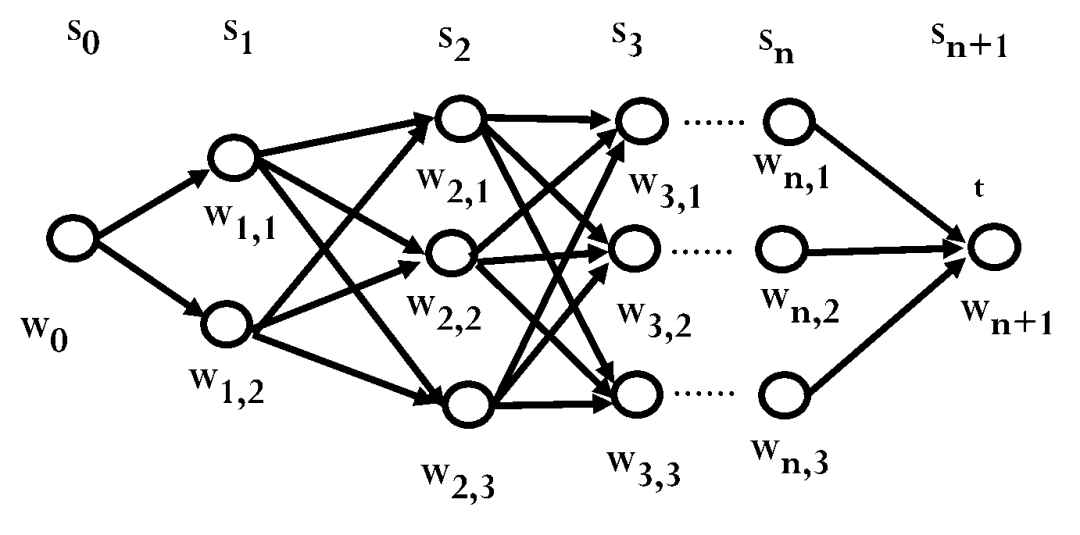
图3.31 篱笆型有向图示意图
艾博士：Viterbi算法是求解该类问题的有效算法，Viterbi算法按列从左向右依次计算到达每个节点的最短路径，直到求得到达 wn+1 的最短路径为止。
以图3.31为例，先计算到达 w1,1、w1,2 两个节点的最短路径，由于到达这两个节点都只有一条路径，所以最短路径分别为 w0-w1,1、w0-w1,2 。接下来计算到达第2列 w2,1、w2,2、w2,3 三个节点的最短路径。对于w2,1 来说，可以通过 w1,1 到达，也可以通过 w1,2 到达，我们从两条路径中选取一个最小代价的路径作为到达 w2,1 的最短路径。由于前面已经求出了到达 w1,1 的最短路径，所以通过 w1,1 到达w2,1 的最短路径代价为到达 w1,1 的最短路径代价加上w1,1 和 w2,1 之间的代价，这样就求出了通过 w1,1 到达 w2,1 的最短路径。同样的方法可以计算出通过 w1,2 到达 w 2,1的最短路径代价。从两个最短路径中选取一个代价最小的路径就得到了到达 w2,1 的最短路径，并记录该路径是通过 w1,1 还是 w2,1 到达的。同样的方法可以求出到达 w2,2、w2,3 的最短路径。依照此方法，利用到达左边一列节点的最短路径计算出到达右边一列节点的最短路径，依次推算下去，就求得了到达终点节点 wn+1 的最短路径，也就是从 w0 到 wn+1 的最短路径。这就是Viterbi算法。
综合以上过程，我们可以得到求解到达每个节点最短路径的递推公式：
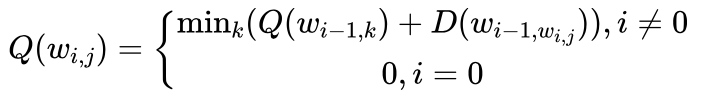
其中 Q(wi,j) 表示从初始节点 w0 到达节点 wij的最短路径的代价，D(wi-1,k , wi,j) 表示节点 wi-1,k到节点 wi,j 的代价。
小明：大概理解了Viterbi算法的求解过程，可以举一个具体的求解例子吗？
艾博士：好的，我们下面就给一个具体的求解例子，问题如图3.32所示。
从S到a、b两个节点都只有一条路径，所以到a的最短路径为S-a，到a的最短路径长度Q(a)=3，到b的最短路径为S-b，Q(b)=5。
到达节点c有两条路径，通过a到c的路径为S-a-c，路径长度为Q(a)+D(a,c)=3+4=7，通过节点b到c的路径为S-b-c，路径长度为Q(b)+D(b,c)=5+1=6。两条路径中S-b-c的长度6更短，所以Q(c)=6。
到达节点d也有两条路径，分别是S-a-d、S-b-d，路径长度分别为5和8，前者更短，所以有Q(d)=5。
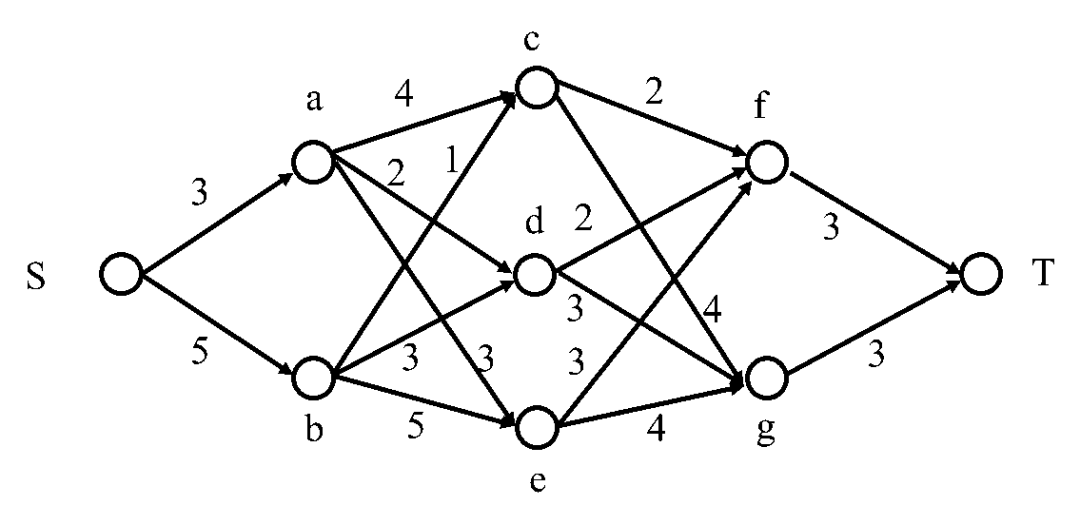
图3.32 Viterbi算法示意图
到达节点e也有两条路径，分别是S-a-e、S-b-e，路径长度分别为6和10，前者更短，所以有Q(e)=6。
至此得到了到达第2列c、d、e三个节点的最短路径。
再看第3列f、g两个节点。有三条路径可以到达f节点，分别通过节点c、d、e。对于通过c到达f的路径长度为Q(c)+D(c,f)=6+2=8，通过d到达f的路径长度为Q(d)+D(d,f)=5+2=7，而通过e到达f的路径长度为Q(e)+D(e,f)=6+3=9。三条路径中通过节点d到达f的路径最短，其路径长度为7，所以该条路径为到达f的最短路径，Q(f)=7。
同理我们可以得到通过节点d为到达g的最短路径，其路径长度为8，所以有Q(g)=8。
最后，到达目标节点T有两条路径，分别经过节点f、g。对于通过节点f到达T的路径，其长度为Q(f)+D(f,T)=7+3=10，而对于通过节点g到达T的路径，其长度为Q(g)+D(g,T)=8+3=11。两条路径中，通过节点f到达T的路径最短，其路径长度为10，所以我们有Q(T)=10。
到此，我们就求得了从初始节点S到达目标节点T的最短路径为S-a-d-f-T，其路径长度为10。
讲解完例题之后，艾博士总结说：Viterbi算法求解最优路径问题最主要的思想就是充分利用第i列已经求得的节点的最优路径，计算第i+1列节点的最优路径，从而有效提高了算法的求解效率。
初学者容易犯的错误是，求到达第i列第j个节点的最优路径时，又从头开始计算求解，没有利用第i-1列已经求解的结果，从而导致求解效率低下。
小明读书笔记
动态规划是求解决策过程最优化的一种方法，Viterbi算法是其中一种常用的算法，是针对篱笆型有向图最短路径问题而提出的一种有效方法。
Viterbi算法从左到右一列列地求解到达每列节点的最短路径，其核心思想是利用左边已有的结果，计算紧邻的右边节点的最短路径，通过递推的方法达到高效求解的目的。这是Viterbi算法最大的特点。
未完待续