第二篇 计算机是如何学会下棋的（二）

清华大学计算机系 马少平

第二节：极小-极大模型

艾博士接着问小明：你会下象棋，请说说你在下棋时是如何考虑走哪步棋的？

小明说：在轮到我行棋时，我会考虑有哪几种下法，再考虑对于我的每种下法对方会如何考虑，我再如何考虑……，然后看几步棋之后的局面如何，我再选择一个我认为好的走步。我水平不太行，大概只能考虑4、5步棋，听说那些职业棋手能考虑到7、8步呢。

艾博士：你的这个思考过程可以用图2.5来示意。图中最上方的方框表示当前棋局，轮到甲方行棋，甲方考虑自己有a和b两种走法，下一步轮到乙方行棋，针对棋局a，乙方可以有c、d两种走法，而对于b，乙方可以有e、f两种走法。下一轮又该轮到甲方行棋……。假设甲方只思考了4步棋，则形成了图2.5的搜索图，最后一行就是双方四步后可能出现的棋局。从甲方的角度来说，他希望最后走到一个对自己有利的局面，而对乙方来说他也希望走到一个对乙方有利的局面。

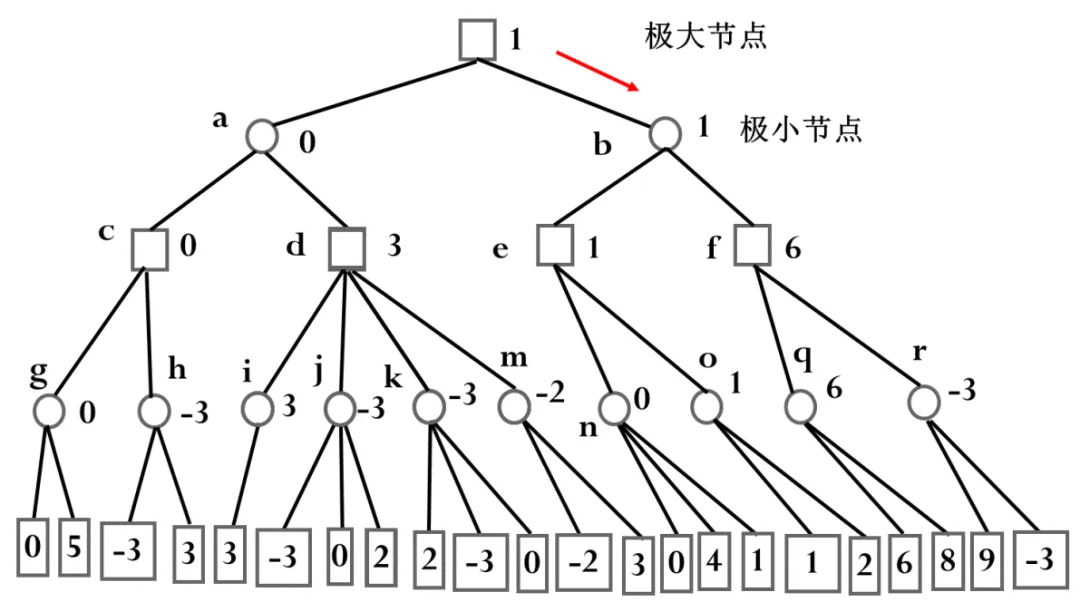
图 2.5 极-小极大模型示意图

假设局面是否有利可以用一个分值表示，大于0的分值表示对甲方有利，而小于0的分值表示对乙方有利，等于0则表示双方势均力敌，是一个双方都可以接受的局面。我们从倒数第二行的圆圈开始考虑，这一行应该轮到乙方行棋。比如对于节点g，乙方可以有两个选择，一个可以得到分值0，一个可以得到分值5。由于分值越小对乙方越有利，所以乙方肯定会选择走获得0分值的那一步，而不会选择走获得5分值的那一步。对于节点h也同样，乙方肯定会选择获得-3分值的那一步。这一行的其他节点也一样，都是从其子节点中选择获得分值最小的那步棋。所以我们可以总结为，对于这一层来说，乙方总是选择具有极小值的节点作为自己的走步。图中倒数第二行节点边标的数字就是乙方所获得的分值。

我们再看倒数第三行的方框，这一行应该轮到甲方行棋。甲方刚好与乙方相反，他肯定会选择子节点中分值最大的那步棋。比如对于节点c，甲方可以选择走到g，可以获得0分值，也可以选择h获得-3分值。由于分值越大对甲方越有利，甲方只会选择行棋到g获得0分值，而不会选择h获得-3分值。这一行的其他节点也同样，图中标出了其他节点可以获得的分值。

最后我们再看a、b两个节点。这两个节点又轮到乙方行棋。乙方同样会从其子节点中选取分值小的节点作为走步，这样a可以获得0分值，b可以获得1分值。而a和b是当前局面下可能的两个选择。如果选择a，无论对方如何行棋，甲方都可以获得至少0分值，如果选择b，无论对方如何行棋，甲方都可以至少获得1分值。虽然0分值对于甲方也是可以接受的，但是1分值结果会更好。所以经过这么一番思考后，甲方决定如图2.5中红色箭头所示的，选择行棋到b。这是一个模仿人类下棋的过程，小明，你下棋时是不是也是类似这样考虑的？

小明说：确实是差不多，只是对于最后可能形成的局面我并没有计算什么分值，只是大概估计一下是否对我有利。

艾博士说：这里之所以用数字表示，一方面是为了量化局面的有利程度，另一方面是为了以后用到计算机下棋上，计算机处理的话，必须表示为数字。

艾博士又进一步讲解说：由于这种方法一层求最小值、一层求最大值交替进行，所以称作极小-极大模型，是通过模仿人类的下棋过程得到的一个模型。其中求最小值的节点称作极小节点，求最大值的节点称作极大节点。

讲到这里，艾博士又进一步强调说：上面说的这些内容，都是甲方为了走一步棋，而在他大脑内的思考过程，并不是甲乙双方真的在行棋。经过一番这样的思考后，甲方选择一步行棋，等待乙方下完一步棋后，甲方再根据乙方的行棋结果再次进行这样的思考。所以上述极小-极大模型只是描述了甲方走一步棋的过程。

小明又迫不及待地问到：我明白了，难道计算机就是采用这种办法下棋的吗？

艾博士回答说：还不是，因为这样做的话，对于实际的下棋过程计算量还是非常大的。以下国际象棋的深蓝为例，基本上要搜索12步，搜索树的节点数在1018量级，据估算，即便在深蓝这样的专用计算机上，完成一次搜索也需要大概17年的时间，所以这个极小-极大模型只是用来描述这样一种模拟人类下棋的过程，并不能真的用于计算机下棋，一些简单的棋类或许可能可以。

小明读书笔记

人类在下棋的过程中，一般是通过向前考虑若干步的方法找到自认为比较好的走法。受人类棋手下棋过程的启发，提出了计算机下棋的极小-极大模型。该模型是在有限搜索深度内穷举出所有可能的状态，从中找出一个在该搜索深度内的最好走法。

由于搜索深度越深计算机下棋的水平越高，极小-极大模型虽然限制了搜索的深度，但是对于真实的棋类问题，要达到与人类大师抗衡的水平，还是因为计算量过大，耗时过多而不能满足实际要求。以深蓝为例，搜索深度限制为12步，用极小-极大方法实现的话，完成一次搜索需要耗时17年时间。这显然是不现实的。

未完待续