第二篇 计算机是如何学会下棋的(一)
清华大学计算机系 马少平
前言
近些年来,人工智能发展很快,再一次掀起了高潮,逐渐渗透到各行各业、各个领域,学习人工智能相关技术的人也越来越多,市面上也出现了很多非常出色的相关书籍。但也经常听到一些朋友抱怨,说这些书太专业了,读起来比较费劲。为此,我利用各种机会写过一些科普文章,介绍人工智能相关的内容,也做过一些科普报告。但也有朋友反馈说,这些科普内容虽然听懂了,但是还是不知道如何实现的,能不能有一本既通俗易懂、又能帮助我们了解具体技术的书,让我们比较容易看懂人工智能究竟是如何实现的。
为此,我思考了很长时间,想写一本能满足这些朋友要求的书。但是几次动笔,都中途而废,写不下去了。这里的关键是如何定位问题。经过很多业内人士、包括我们组内的同学等,在这个过程中给了我很多鼓励和很好的建议,最终我想尝试着写一本有关人工智能入门的初级读物,读者对象定位在具有一定的理工科背景的朋友,用通俗易懂的语言,由浅入深,讲授人工智能的基本原理。在写的过程中,我想到了“一师一生”的具有一定交互的写作方法,书中设计了“艾博士”这样一位博学的老师(“艾”即AI),和一位聪明好学的学生小明,通过二人的对答,讲授人工智能的基本原理和方法。
《计算机是如何实现智能的》计划共由六篇内容组成,每篇内容独立成章。除了文字内容外,每篇内容还配有若干个讲解视频,每段视频在20分钟左右,以利于朋友们学习。
本书作为人工智能的入门性通俗读本,将引领您走进人工智能的世界。
这里推出的是本书的第二篇:计算机是如何学会下棋的。
这是我们的初步尝试,效果如何,还请朋友们多加赐教。欢迎各位朋友留下您宝贵的意见和建议,对于书中出现的任何不当之处或没有说明白的地方,还望不吝赐教,本人将不胜感激。
艾博士导读
下棋一直被认为是人类的高智商游戏,从人工智能诞生的那一天开始,研究者就开始研究计算机如何下棋。著名人工智能学者、图灵奖获得者约翰·麦卡锡在50年代就开始从事计算机下棋方面的研究工作,并提出了著名的α-β剪枝算法。很长时间内,该算法成为了计算机下棋程序的核心算法,著名的国际象棋程序深蓝采用的就是该算法框架。
1996年,正值人工智能诞生40周年之际,一场举世瞩目的国际象棋大战在深蓝与卡斯帕罗夫之间举行,可惜当时的深蓝功夫欠佳,以2:4的比分败下阵来。1997年,经过改进的深蓝再战卡斯帕罗夫,这次深蓝不负众望,终于以3.5:2.5的比分战胜卡斯帕罗夫,可以说是人工智能发展史上的一个里程碑事件。
到了2006年,为了庆祝人工智能诞生50周年,中国人工智能学会主办了浪潮杯中国象棋人机大战,先期举行的机器博弈锦标赛获得前5名的中国象棋系统,分别与汪洋、柳大华、卜凤波、张强、徐天红5位中国象棋大师对弈,人机分别先行共战两轮10局比赛,双方互有胜负,最终机器以11:9的总成绩战胜人类大师队。
转眼到了2016年,又值人工智能诞生60周年,人工智能的发展已不可同日而语,呈现出蓬勃发展之势。沉默多年的计算机围棋界突然冒出个AlphaGo,先是4:1战胜韩国棋手李世石,转年又战胜我国的柯洁。至此,在计算机下棋这个领域,机器已经完全碾压人类棋手,机器战胜人类最高水平棋手已无任何悬念。
三次重要事件均与人工智能提出的秩年有关,三大棋类机器战胜人类顶级棋手的时间顺序也刚好与三大棋类可能出现的状态数的多少一致,这也许只是一种巧合,在本篇正文中你可以看到,状态数的多少并不是棋类难度的主要问题。
那么计算机是如何学会下棋的呢?本篇将逐一解开这个谜团。
本篇内容按照难易程度划分为三个等级,读者可以根据自身需要有选择的读其中几节或者全部内容。
第一级:2.1节到2.4节,主要介绍有关计算机下棋的基础模型,以及α-β剪枝算法、蒙特卡洛树搜索算法。这两个算法构成了当今两个主要的计算机下棋的算法框架,也刚好构成了深蓝和AlphaGo的主要算法框架。
第二级:2.5节,主要介绍AlphaGo的实现原理,通过这一节的学习,读者可以完全掌握AlphaGo战胜人类围棋大师的奥秘。在阅读这一节之前,需要读者掌握有关深度学习、神经网络方面的有关知识,如果你还不具备相关知识,请先阅读本书第一篇《神经网络是如何实现的》。
第三级:2.6节、2.7节,先介绍深度强化学习的有关概念,然后结合计算机围棋的特点,介绍三种典型的计算机围棋中用到的强化学习方法,最后介绍AlphaGo Zero的实现原理,这是一种从零学习的方法,通过自我博弈,利用强化学习方法逐步提高计算机下棋的水平。同第二级一样,需要读者掌握深度学习、神经网络方面的相关知识,如果你还不具备相关知识,请先阅读本书第一篇《神经网络是如何实现的》。
时间定位在2016年3月9日,这一年是人工智能诞生60周年,一场世界瞩目的围棋人机大战正在李世石与AlphaGo之间展开。韩国棋手李世石曾经10次获得过世界冠军,是当今世界上最优秀的围棋手之一,而AlphaGo是谷歌公司旗下的人工智能实验室DeepMind最新推出的围棋系统,在此之前DeepMind曾经在多个游戏人机大战中战胜过人类,因此这场人机大战受到了世界范围的广泛关注。6天以后的3月15日,经过5场比赛之后,AlphaGo以4:1的比分完胜李世石。一年以后,水平更高的AlphaGo Master又战胜了世界排名第一的我国棋手柯洁,轰动了世界。

图2.1 李世石、柯洁分别对战AlphaGo
小明是一位人工智能爱好者,平时就比较喜欢下棋,全程观看了比赛后非常兴奋,求知的欲望又涌现了出来:计算机究竟是如何学会下棋的呢?带着这个疑问,小明又找到了万能的艾博士,请艾博士讲讲这个问题。
第一节:能穷举吗?
艾博士一见到小明,就猜出了他的来意:小明,这几天看了李世石与AlphaGo的人机大战了吧?有什么感想?
小明忍不住说道:艾博士,我看了全部比赛的传播,真是太震撼了,没有想到计算机下棋水平发展的这么快。
艾博士:这次AlphaGo以4:1战胜李世石确实出乎很多人的意外,因为围棋被认为是计算机下棋中最难的问题,可以说是计算机下棋的最后一个堡垒被攻克了。
小明:最后一个堡垒?以前计算机也战胜过人类下棋大师吗?

图2.2 卡斯帕罗夫与深蓝对弈
艾博士:1997年IBM的深蓝,一台会下国际象棋的计算机,就首次在正式比赛中以3.5:2.5的比分战胜了国际象棋大师卡斯帕罗夫,卡斯帕罗夫是当时国际上最顶尖的国际象棋大师,曾经连续十年获得国际象棋比赛的世界冠军。
小明:1997年就有了这样的成绩啊,那时我还没有出生呢。
艾博士:2006年为纪念人工智能诞生50周年,中国人工智能学会主办了浪潮杯中国象棋人机大战,先期举行的机器博弈锦标赛获得前5名的中国象棋软件,分别与汪洋、柳大华、卜凤波、张强、徐天红5位中国象棋大师对弈,人机分别先行共战两轮10局比赛,双方互有胜负,最终机器以11:9的总成绩战胜人类大师队。

图2.3 浪潮杯中国象棋人机大战
左图:比赛前的记者见面会,右图:5人同时在对局室内对战
小明:这次的人机大战有5个不同的软件参赛啊?看来普遍水平都很高啊。但是计算机是如何学会下棋的呢?
艾博士:小明你先别着急,我们先看一个“分钱币”游戏的例子。
分钱币游戏是这样的,桌上有若干堆钱币,每次对弈的一方选定一堆钱币,并将该堆钱币分成不等的两堆,这一过程称为行棋。甲乙双方轮流行棋,直到有一方不能行棋为止,则对方取胜。图2.4给出了初始状态为8个钱币的例子,图中给出了该问题所有可能的走法。
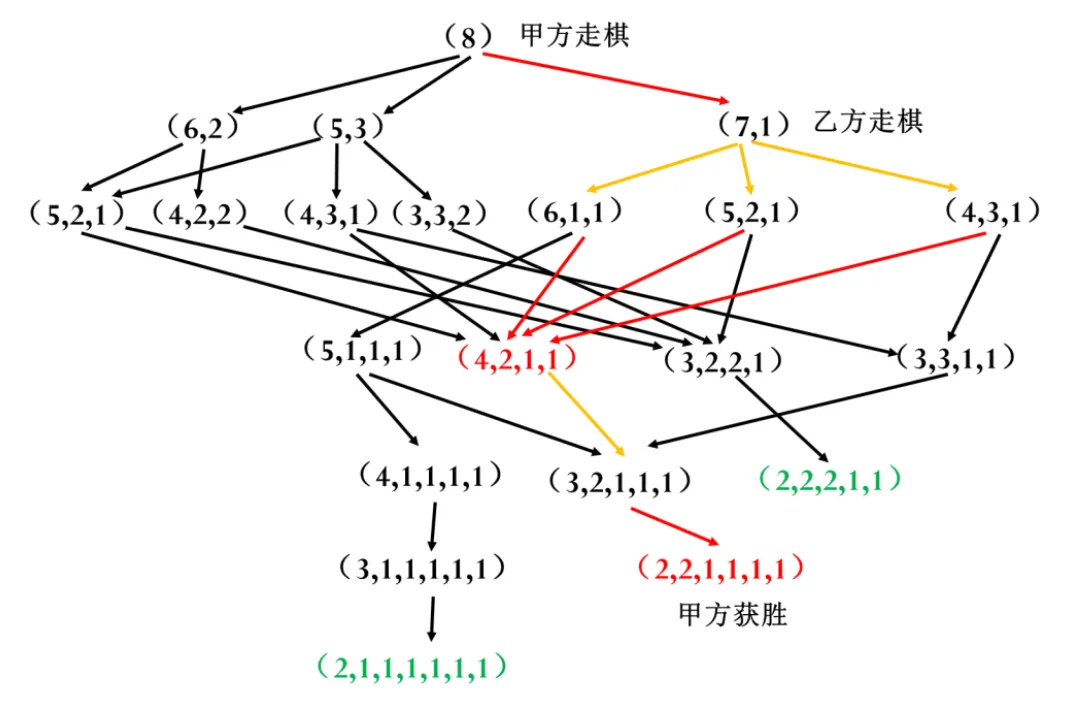
图2.4 分钱币问题状态图
假设甲方先行行棋,甲方可以将8枚硬币分成(6,2)两堆,或者(5,3)两堆,或者(7,1)两堆,但不能分成(4,4),因为这是分成了相等的两堆,这是规则所不允许的。下一步轮到乙方行棋,“1”这堆不能选,因为无法分成两堆,“2”这堆也不能选,因为不能分成不相等的两堆,“6”、“5”、“7”都是可选的,但是要注意“6”只能分成(4,2)或者(5、1),而不能分成(3,3),因为(3,3)是相等的两堆。按照这样的原则,我们在图2.4中给出了所有可能的行棋方法。
艾博士问小明:你能看出什么规律吗?
小明看了看摇摇头说:还看不出有啥规律。
艾博士指着图说:甲方如果按照红色箭头走成(7,1),则乙方只能选择“7”这堆,将“7”分成(6,1)或者(5,2)或者(4,3),也就是图中按照黄色箭头得到(6,1,1)、(5,2,1)、(4,3,1)。无论对于这三种情况的哪一种,甲方都可以按照红色箭头选择行棋到(4,2,1,1),比如乙方行棋到了(6,1,1),则甲方将“6”分成(4,2),如果乙方走的是(5,2,1),则甲方将“5”分成(4,1)即可。而一旦甲方走到了(4,2,1,1),则乙方只能行棋到(3,2,1,1,1),这时甲方只需将“3”分成(2,1),得到(2,2,1,1,1,1),则乙方无棋可走,必输无疑。也就是说,对于这样一个分钱币游戏,甲方是存在必胜策略的。
小明恍然大悟道:还真是这样啊,只要甲方走棋正确,乙方无论如何是不可能获胜的。难道计算机下棋依靠的就是这种穷举方法找到必胜策略吗?
艾博士马上说:不是这样的。对于分钱币游戏这样的简单问题,或者再稍微复杂一点的游戏,依靠穷举所有可能的方法也许可以找到必胜策略,但是对于象棋、围棋这样的变化非常多的棋类,是不可能穷举其所有可能性的。这也是目前在一些人中存在的误解,认为现在计算机速度这么快,存储这么大,对于国际象棋、中国象棋这样的棋类,完全可以依靠穷举战胜人类。其实这是非常错误的看法。
小明不解地问到:我也听说过这种说法,但是为什么是错误的看法呢?
艾博士回答说:我们以中国象棋为例分析一下。在考虑不同的走棋顺序的情况下,总的状态数大约为 10^150 ,假设1毫微秒可以产生一个状态,则产生出这些状态大约需要 10^134 年。这是什么概念呢?从存储上考虑,地球上的原子总数约 10^50个,如果一个原子可以存储一个状态的话,则需要 10^100 个地球才有可能存储得下这些状态。从时间上考虑,按照宇宙大爆炸的理论推算,宇宙年龄大概为1.38*10^10 年,假设从宇宙诞生那一刻起就有一台高速计算机以每毫微秒生成一个状态的速度在运算,到目前为止也只产生了其中的1.38*10^-124 %,也就是0.000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000138%。
小明听着艾博士的讲解惊愕到:中国象棋的状态数竟然有这么大啊,看来依靠穷举所有可能的状态获得必胜策略的想法是行不通的。
艾博士接着讲解说:国际象棋的状态数稍微少一些,但也没有质的差别,围棋状态数则更多。所以结论就是不能靠穷举出所有可能状态的方法找到必胜的行棋策略。
小明读书笔记
棋类历史上有过三次著名的人机大战事件。大家对计算机围棋系统AlphaGo战胜李世石、柯洁,计算机国际象棋系统深蓝战胜卡斯帕罗夫比较熟悉,在这两次人机大战之间,我国的五套计算机中国象棋系统战胜了人类五位中国象棋大师,也是人工智能发展史上的一件大事。
在一些人中经常有这样的误解:认为现在计算机速度这么快,存储这么大,对于国际象棋、中国象棋这样的棋类,计算机完全可以依靠穷举出其所有可能状态的方法战胜人类,这是非常错误的看法。无论是国际象棋还是中国象棋,由于其可能出现的状态数过于庞大,是不可能通过穷举所有可能状态的方法找到必胜策略的。三次人机大战均与人工智能提出的秩年有关,三大棋类机器战胜人类顶级棋手的时间顺序也刚好与三大棋类可能出现的状态数的多少一致(按照可能的状态数多少从小到大排序依次为国际象棋、中国象棋和围棋),这也许只是一种巧合。
未完待续

