第五篇 统计学习方法是如何实现分类与聚类的(十六)
清华大学计算机系 马少平
第十六节:
DBSCAN聚类算法
艾博士:在实际应用中,采集的数据往往是带有噪声的,噪声对聚类结果可能会带来很大的影响,严重影响聚类效果。如图5.59所示,彩色样本点的数据比较可靠,黑色样本点大概率是噪声数据。另外,从直观上看,相同颜色的样本点应该属于同一个类别,聚集后每个类别的形状也存在很大的不同,前面介绍的一些方法难于胜任这种情况下的聚类问题。
观察图5.59中数据的分布情况,数据有梳有密,不同区域包含的样本点的密度不同,我们有理由认为处于密度大的区域的样本应该聚集成一个类别,而处于过于稀疏区域的样本点,大概率属于噪声点。这样就提出了基于密度的聚类算法,DBSCAN是其中的典型代表,不仅可以实现对包含不同“形状”样本的聚类,还可以同时消除噪声样本,是一种常用的聚类算法。
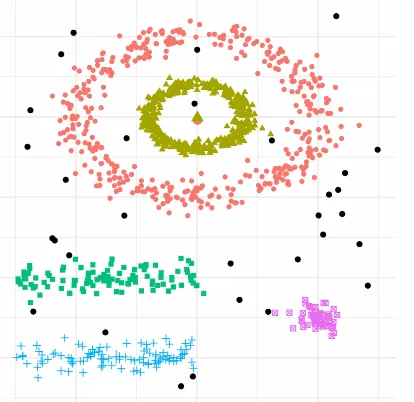
图5.59 不同类别形状并带有噪声的样本示意图
小明:这是一个很有意思的想法。我们看图5.59,之所以认为每种颜色的样本应该组成一个类别,很大程度上是利用了样本分布的密度信息。但是计算机处理问题容易“只见树木不见森林”,DBSCAN算法是如何实现基于密度的聚类呢?
艾博士:为了便于说明,我们先介绍几个基本概念。
(1)核心样本。以某个样本p为圆心、r为半径做圆,如果包括该样本在内圆内至少包含有minPts个样本,则称p为核心样本。圆内的任一样本q称作被p包含,或者说q相对p来说直接可达。其中r、minPts为事先给定的参数。核心样本的物理含义是说明该样本处于一个密度比较高的区域,被核心样本包含的样本应该同属一个类别。
(2)异常样本。如果一个样本既不是核心样本,也不被任何核心样本所包含,则称该样本为异常样本。异常样本说明该样本处于一个比较稀疏的区域,大概率是一个噪声样本。
图5.60给出了一些样本,并以每个样本为圆心、r为半径做圆,为了看起来更直观,图中圆心和圆用了相同的彩色。我们假设minPts为3,则从图中可以看出,c、d、e、f、j、k这几个样本均至少包含了3个样本,所以属于核心样本。a、b、h、n这几个样本包含的样本数均少于3个,而且没有被任何核心样本所包含,所以属于异常样本。g、i、m这几个样本虽然包含的样本也少于3个,但是由于它们被核心样本所包含,所以不属于异常样本,当然也不属于核心样本。

图5.60 核心样本、异常样本示意图
DBSCAN算法的核心思想是,先选取一个核心样本p,将p所包含的所有样本加入到类c中,标记样本p被处理过。从类c中依次选取没有处理过的核心样本q,并将q所包含的样本加入到类c中,标记样本q被处理过。在这个过程中,类c中的样本逐渐增加,新增加的样本有核心样本也有非核心样本。重复以上过程,直到类c中所有核心样本被标记处理过,则完成了第一个类别的聚类,类c中的所有样本为一个类别。再选取一个没有被处理过的核心样本,按照上述方法完成第二个类别的聚类。依次进行下去,直到最后所有的核心样本被处理完,则结束聚类,剩下的异常样本当作噪声被过滤掉。
下面我们以图5.60所示的样本分布为例,说明DBSCAN算法是如何实现聚类的。
假设首先选取的核心样本为c,将c及c包含的样本d、e合并在一起算作类别1,并标记c被处理过。从类别1中选取一个没有被处理过的核心样本,假设是样本d。将d包含的样本c、e加入到类别1中,由于这两个样本已经在类别1中,所以不做操作,标记d被处理过。再次从类别1中选取一个没有被处理过的核心样本,假设是样本e。e包含的样本中只有样本f没有在类别1中,将样本f加入到类别1中,标记e被处理过。接着从类别1中选择核心样本f,将被f包含而且没有在类别1中的样本g加入到类别1中,标记f被处理过。由于g不是核心样本,所以此时类别1中已经没有未被处理过的核心样本,到此我们得到了第一个聚类结果,类别1中包含了样本c、d、e、f、g。
选择一个未被处理过的核心样本,假设是j,将j包含的样本i、j、k一起组成类别2,标记j被处理过。从类别2中选择一个核心样本,由于i不是核心样本,所以只能选择k,将k包含并且没在类别2中的样本m加入到类别2中,标记样本k被处理过。此时类别2中已经不存在未被处理过的核心核心样本,所以聚类结束,得到第二个聚类结果,类别2中包含了样本i、j、k、m四个样本。
至此所有的核心样本均已经被处理,得到了聚集而成的两个类别。剩余的样本a、b、h、n均为异常样本,不在任何聚类结果中,算法结束。
小明:通过算法介绍和例题讲解我明白了DBSCAN算法的聚类过程,简单说就是以一个核心样本为基础,把该核心样本所包含的样本加入到一个类别中,然后再一步步地将该类别中其他核心样本所包含的样本也加入到这个类别中,直到该类别中所有的核心样本均被处理过为止,这样就完成了一个类别的聚类。然后再按照同样的方法,完成所有类别的聚类。在这个聚类过程中似乎没有要求事先知道类别数K,DBSCAN算法可以自动获取类别数K吗?
艾博士:小明你观察得很仔细,DBSCAN算法确实不需要知道类别数K就可以实现聚类。我们前面提到过,任何聚类算法或者需要知道类别数K,或者转化为了其他的参数。DBSCAN算法虽然不需要类别数K,但是要事先定义圆的半径r和核心样本包含的最小样本数minPts,这两个参数对最终获得的聚类结果和类别数会产生影响,不同的取值会有不同的结果。
小明思考了一会儿说:确实是这样的,以图5.60为例,如果minPts为2的话,那么a、b就可以聚为一类,就多了一个类别。如果r再小一点的话,类1或者类2被分为两个类别也是有可能的。
小明读书笔记
DBSCAN算法是一种基于密度的算法,按照数据分布的密度,实现不同“形状”的聚类,可以消除噪声,减少噪声数据对聚类结果的影响。
该算法需要设定一个半径r以及圆内至少包含的样本数minPts。以一个样本为圆心r为半径画圆,如果圆内包含至少minPts个样本,则该样本称作核心样本。
DBSCAN算法的核心思想是,选取一个核心样本,将该样本所包含的所有样本作为一个类别。如果类别中还有其他的核心样本,则将这些核心样本包含的其他样本也加入到这个类别中,直到类别中所有的核心样本都被处理完,则完成了一个类别的聚类。再选择其他的没有处理过的核心样本完成下一个类别的聚类,直到所有的核心样本被处理完。剩余的没有被任何类别所包含的样本则认为是噪声样本。
未完待续

