第三篇 计算机是如何找到最优路径的(三)
清华大学计算机系 马少平
第三节:迪杰斯特拉算法
小明:在单位代价下,宽度优先搜索算法可以找到代价最小的路径,但是很多问题并不是单位代价的。比如说对于八数码问题,如果移动将牌的代价为将牌的数码,如数码为5的将牌移动一次的代价为5,每个将牌的数码不一样,移动的代价也不相同。再比如,如果步行或者骑车去某个地方,相对于红绿灯最少来说,可能距离最短更重要。即便是开车,距离也是一个重要的影响因素。那么是否有办法求解一般情况下总代价最小路径的方法呢?
艾博士反问小明:小明,宽度优先搜索是如何选择被扩展节点的?
小明马上回答说:优先选择深度最浅的节点扩展。
艾博士:小明回答的很好。如果我们用g(n)表示从初始节点到节点n的一条路径的代价,节点n的深度就相当于单位代价下的g(n)。所以,宽度优先搜索优先选择深度浅的节点,就相当于单位代价条件下优先选择g(n)小的节点扩展。我们修改一下宽度优先搜索算法,优先选择g(n)小的节点扩展,宽度优先搜索算法就变成了迪杰斯特拉算法。但是需要修改一下结束条件:当目标节点的g(n)值最小时,算法才结束,而不是只要目标一出现就马上结束。
小明问:为什么要加上这样的条件呢?
艾博士:这个条件很关键,我们后面再讲为什么要有这样的条件。
我们还是通过图3.2的例子介绍迪杰斯特拉算法,为了看起来方便,我们将图3.2的状态连接图重画在下面的图3.9中,图3.10给出了该问题的搜索图。同样,红圈里的数字表示节点被扩展的顺序,连接线旁边的数字表示的是两个节点间的距离。
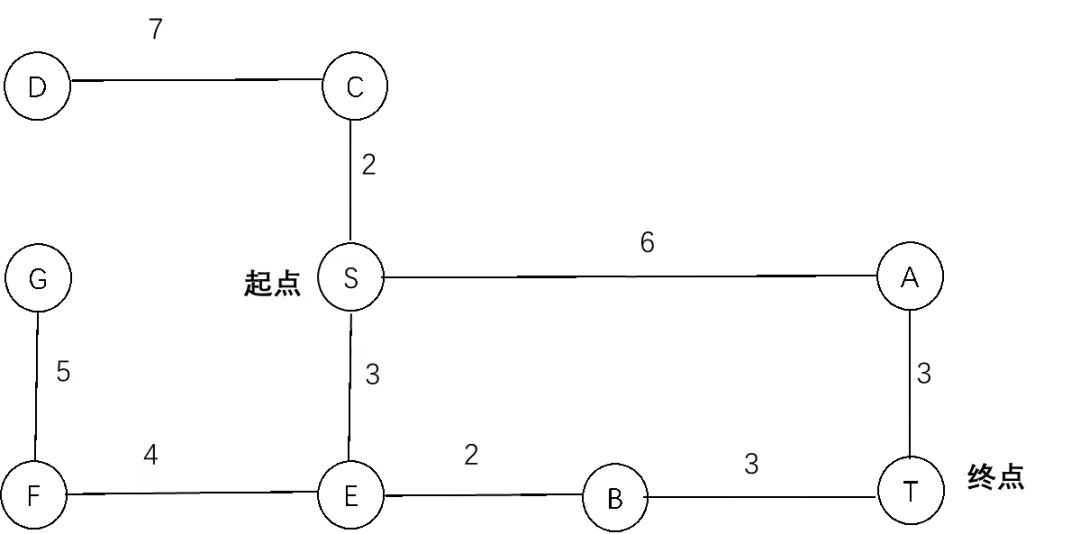
图3.9 状态连接图示意
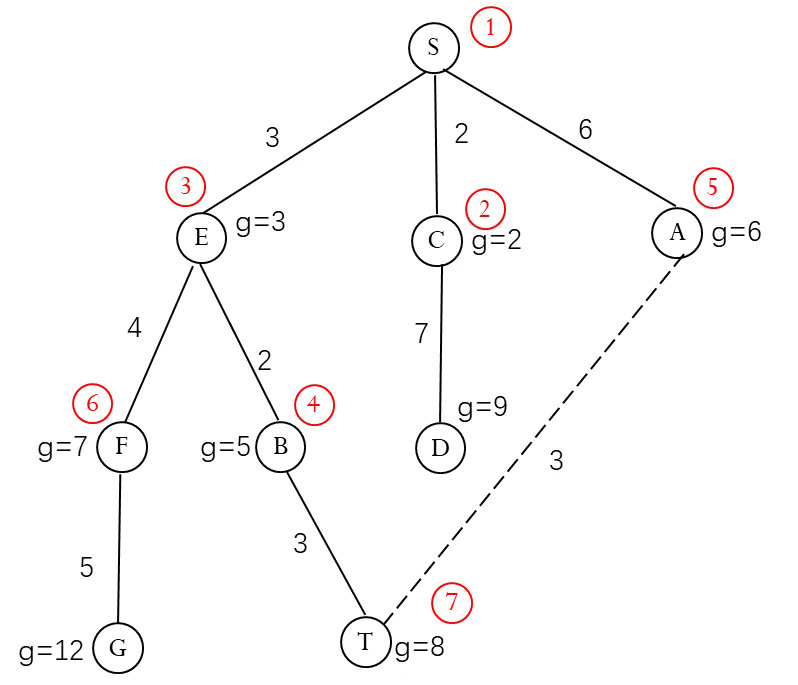
图3.10 迪杰斯特拉算法搜索示意图
在图3.10中,首先扩展初始节点S,生成出节点A、E、C,按照S到这三个节点的距离,分别得到:
g(A) = 6
g(C) = 2
g(E) = 3
由于g(C)最小,所以第二次选择C扩展,生成出节点D,并得到g(D)=g(C)+7=9。
接下来从A、D、E中选择一个g值最小的节点,g(E)=3被选中第三个扩展,产生节点B、F,分别计算出:
g(B) = 5
g(F) = 7
在A、D、B、F几个节点中,g(B)=5最小,成为第四个被选择扩展的节点,生成出节点T,经计算有:
g(T) = 8
这时虽然已经找到一条从初始节点S到目标节点T的路径S-E-B-T,但是由于g(T)并不是最小的(g(A)=6、g(F)=7均小于g(T)=8),所以算法并不停止,继续选择g值最小的节点扩展。
接下来第五个被选择扩展的节点是A,再一次生成出节点T。这时找到了两条到达T的路径,一条是之前找到的S-E-B-T,另一条是刚找到的S-A-T。这种情况下,需要做一次选择,保留代价最小的路径,由于通过路径S-E-B-T计算g(T)为8,而通过路径S-A-T计算g(T)为9,所以保留前者,而忽略后者,图中用虚线表示。
这时g(F)又成为了最小的,所以第六次选择节点F扩展,生成出节点G,并计算g值为:
g(G) = 12
这时,已经生成但还未被扩展的节点有F、G、T,三个节点中T的g值最小,而T又是目标节点,算法结束。
这样就找到了从初始节点S到达目标节点T的路径S-E-B-T。
小明:艾博士,迪杰斯特拉算法每次选择g值最小的节点扩展,当问题是单位代价时,与宽度优选搜索算法是等价的。那么在一般情况下,迪杰斯特拉算法一定能够找到最小代价的路径吗?
艾博士:可以证明,迪杰斯特拉算法可以找到代价最小的路径。即便不满足单位代价条件,找到的也一定是代价最小的路径。
但是一定要记住前面我们提到过的迪杰斯特拉算法的结束条件,当目标节点的g(n)值最小时,算法才结束。这是迪杰斯特拉算法能找到最小代价路径的一个重要条件。因为迪杰斯特拉算法总是从搜索图的叶节点(即搜索图中已经产生但是还没有被扩展的节点)中选择一个节点扩展,当目标节点的g值最小时,其他节点还没有到达目标节点,其g值就已经比目标节点的g值大了,所以通过其他节点到达目标节点的路径代价肯定不会比目前得到的这条路径小,从而找到的一定是代价最小的路径。不过这里也需要做一个补充说明,即代价都是大于0的,不存在负的代价。
小明还是有些不太明白地问到:在上面的例子中,最初就找到了路径S-E-B-T为什么不能马上结束呢?最终找到的最短路径也是这一条路径啊。
艾博士解释说:小明你看图3.10所示的搜索图,图中虚线部分的代价如果不是3而是1,会出现什么情况?这时从S到T的最短路径应该是S-A-T,而非S-E-B-T,如果开始找到了S-E-B-T就马上停止,还能找到最短路径吗?
小明想了想明白了:确实是这样的,所以迪杰斯特拉算法的这个结束条件是必须有的,否则就不能保证找到最优路径。
艾博士进一步补充说:我们还需要强调一下,一般介绍迪杰斯特拉算法时,叙述方法可能与我们这里介绍的不太一样,但是其核心思想是一样的。我们之所以这样讲解,主要是为了从宽度优先搜索算法扩展到迪杰斯特拉算法,后面还要将再次扩展到启发式搜索方法,将这几个方法采用同一个框架连贯、统一起来。事实上,宽度优先搜索算法没有利用两个节点间的代价信息,所以只能在单位代价下找到最优路径。而迪杰斯特拉算法利用了两个节点间的代价信息,适应面更加广泛,在非单位代价情况下,也同样能找到最优路径。
小明读书笔记
迪杰斯特拉算法充分利用了到达每个节点的代价信息,优先选择代价最小的节点扩展,即便问题是非单位代价时,也可以找到最优路径。需要强调的是,当被选择扩展的节点是目标节点时算法才结束,而不是一发现目标节点马上就结束,只有这样才能保证算法找到最优解。
未完待续

