第二篇 计算机是如何学会下棋的(七)
清华大学计算机系 马少平
第七节: AlphaGo Zero是如何自学成才的
艾博士继续介绍说:AlphaGo Zero是继AlphaGo之后的一个升级版本,完全抛弃了人类数据,实现了从零学习,这也是其名称的由来,英文“Zero”是零的意思。
小明不解地问:从零学习是什么意思呢?
艾博士:AlphaGo有策略网络和估值网络两个神经网络,训练时用到了大约16万盘的人类棋谱,虽然也用到了一些深度强化学习技术,但是主要还是从人类棋谱中学习。而AlphaGo Zero不再用任何人类棋谱,利用深度强化学习方法,从开始的随机下棋开始,不断的总结学习,逐步提高其下棋水平,并且最终达到了远高于AlphaGo的水平。从零学习指的就是在训练过程中不用任何人类提供的相关数据。
小明:这也太神奇了,AlphaGo Zero是如何做到这一点的呢?
艾博士:为了实现从零学习,AlphaGo Zero从总体框架上做了一些改进,在构建策略网络和估值网络时,采用了性能更好的残差网络ResNet,并且将策略网络和估值网络整合在一起构建了一个“双头”神经网络,即同时包含策略网络输出和估值网络输出两个“头”,而共用残差网络组成的神经网络“体”。又将深度强化学习与蒙特卡洛树搜索紧密地结合在一起,使得深度强化学习更加有效。
小明着急地说:艾博士,您就快讲讲是如何改进的吧,我都有点等不及了。
艾博士:小明,着急吃不了热豆腐,我们一点一点地讲起。小明,先问问你,策略网络和估值网络各自的功能是什么?
小明回忆了一下说:这两个网络输入的都是当前棋局,策略网络输出在每个可落子点行棋的概率,估值网络输出当前棋局的收益。
艾博士:对!我们先看看AlphaGo Zero是如何将这两个网络融合在一起的,为了说明方便,我们将整合后的网络称作策略-估值网络,图2.23给出了策略-估值网络的示意图。
图中上半部分是一个残差网络,组成了策略-估值网络的“体”,称作策略-估值网络体,输入为17个大小为19×19的通道。与AlphaGo的策略网络有48个输入通道和估值网络有49个输入通道不同,AlphaGo Zero的策略-估值网络只有17个输入通道,而且这些通道都是围棋中很自然的特征,排除了一些人为抽取的特征,以体现AlphaGo Zero从零学习的特性。这17个通道分别为:(1)一个通道记录当前棋局黑棋在棋盘上的位置,有黑棋的位置为1,否则为0;(2)一个通道记录当前棋局白棋在棋盘上的位置,有白棋的位置为1,否则为0;(3)用14个通道分别记录前七个棋局,每个棋局用两个通道分别记录有黑棋的位置和有白棋的位置,七个棋局共14个通道。(4)一个通道记录当前的行棋方,轮到执黑棋方行棋则全部填1,轮到执白棋方行棋则全部填0。这样共17个通道,完全是对棋局的自然记录,没有任何人工的处理。
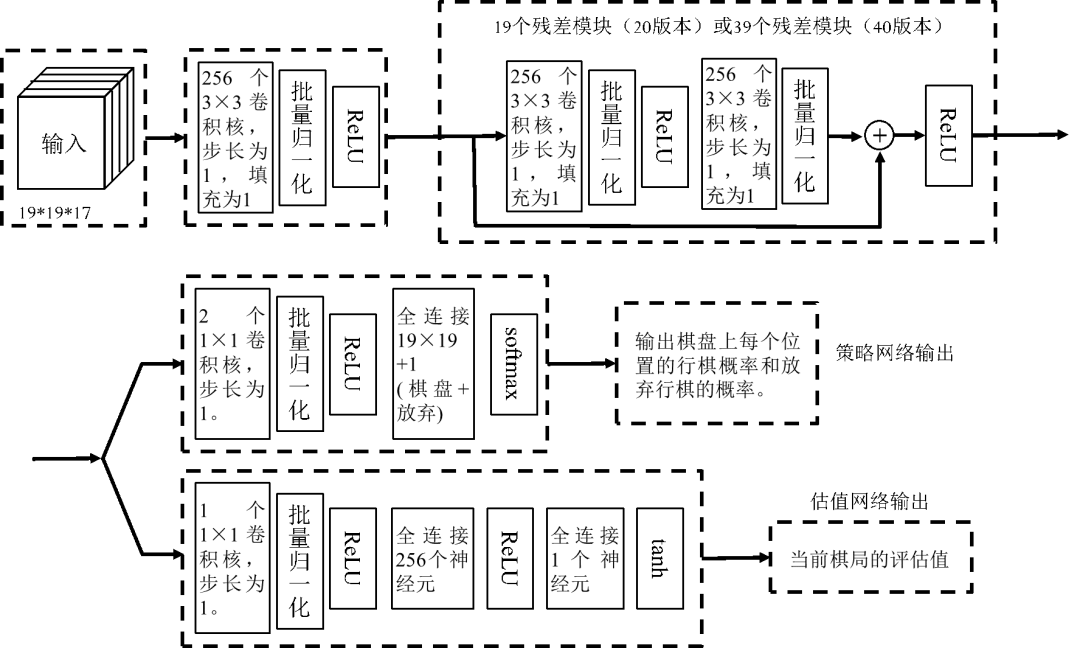
图2.23 策略-估值网络示意图
策略-估值网络的第一层是256个3×3的卷积核,步长为1,填充为1,后接一个批量归一化后再接ReLU激活函数。
小明不解地问:什么是批量归一化呢?
艾博士解释说:这里的批量指的是采用BP算法进行训练时,每次选取的样本个数,在每个批量完成之后,对卷积层的输出做一次均值为0、方差为1的归一化,以防止训练过程中数据产生过大的变化。批量归一化的引入可以有效提高训练速度,并减少过拟合现象的发生。相关内容我们就不讲解了,有兴趣的话可以查看相关资料。
接下来是连续19个残差模块或者39个残差模块,对应AlphaGo Zero的策略-估值网络的两个不同版本。除了组成的残差模块数量不同以外,其他部分都是相同的。每个残差模块由两层卷积网络组成,第一个卷积层为256个大小为3×3的卷积核,步长为1,填充为1,经批量归一化后接ReLU激活函数。第二个卷积层同样是256个大小为3×3的卷积核,步长为1,填充为1,经批量归一化后,与该残差模块的输入相加后再接ReLU激活函数。这是策略-估值网络共用的“体”部分,接下来分成两路分别组成策略网络和估值网路两个“头”部输出。对于策略网络部分来说,其头部由两层组成,第一层是2个1×1的卷积核,步长为1,经批量归一化后接ReLU激活函数,第二层是19×19+1个神经元组成的全连接层,接softmax激活函数后作为策略网络的输出。
小明又有些不明白了,急忙问道:策略网络的输出是在每个可落子点行棋的概率,围棋棋盘大小是19×19,有19×19个输出就可以了,为什么要加1呢?
艾博士解释说:在围棋中,甲乙双方在下棋过程中都可以选择放弃行棋,如果双方都选择了放弃,那么这局棋就结束了。在AlphaGo中何时选择放弃是通过一段程序判断的,AlphaGo Zero为了突出从零学习的特点,尽可能减少人为的干预,“放弃”也作为一步行棋,通过学习获得。所以这里的策略网络的输出就需要多一个,用来表示放弃行棋的概率。
小明:原来是这样啊,我明白了。
艾博士:对于估值网络部分来说,其头部由三层组成,第一层是1个1×1的卷积核,步长为1,经批量归一化后接ReLU激活函数,第二层是256个神经元组成的全连接层,后接ReLU激活函数,最后一层是只有一个神经元的全连接层,经tanh激活函数后得到估值网络的输出。
小明问艾博士:这里为什么要用tanh激活函数呢?
艾博士解释说:估值网络输出的是当前棋局的收益,收益的取值范围在-1、1之间,大于0时表示正的收益,小于0时表示负的收益。所以通过tanh激活函数将估值网络的输出变换到-1、1之间。
小明:我明白了,刚才没有转过弯来。那么这个策略-估值网络是如何训练的呢?
艾博士:小明,我们先假定策略-估值网络已经训练好了,至于如何训练得到的,我们留待后面再说。我们先讲讲AlphaGo Zero是如何将策略-估值网络与蒙特卡洛树搜索相结合实现下棋的。
AlphaGo Zero中的蒙特卡洛树搜索与AlphaGo的基本差不多,只有一个变化,我们只讲这个变化就可以了,其他相同的部分就不再讲解了。
在AlphaGo中,当选择到一个叶节点后,会通过两种办法计算该节点的收益,一个是通过估值网络计算,一个是通过随机模拟获得,并将二者的加权平均值作为该节点的收益。而在AlphaGo Zero中,去掉了随机模拟过程,直接用估值网络的计算结果作为该节点的收益。其他地方基本就与AlphaGo一样了,我们不再详细讲解了。
小明:为什么可以去掉模拟过程呢?
艾博士解释说:在AlphaGo中最后选择要模拟的节点,其收益通过下式将估值网络的计算结果和随机模拟结果进行加权平均获得: 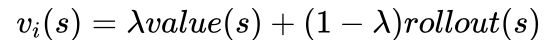
其中value(s)表示通过估值网络计算得到的收益,rollout(s)表示通过随机模拟得到的收益,0≤λ≤1为加权系数。
而在AlphaGo Zero中直接使用估值网络的计算结果作为该节点的收益,相当于λ取1的情况。之所以这么做,是因为AlphaGo Zero的设计者认为估值网络的结果已经足够可信,不再需要进行随机模拟了。这样一来,当需要随机模拟的时候,直接通过估值网络计算就可以了,加快了蒙特卡洛树搜索的速度。
小明想了想说:似乎是很有道理的。

图2.24 AlphaGo Zero中的深度强化学习流程
艾博士:下面我们说说AlphaGo Zero是如何实现深度强化学习的。
在AlphaGo Zero中采用的深度强化学习方法与我们前面介绍过的深度强化学习方法总体上思路差不多,通过自我博弈产生样本,用以训练策略-估值网络,从而提高系统的下棋水平。在以前的AlphaGo的强化学习中,自我对弈只使用了策略网络和估值网络,并通过深度强化学习方法改善策略网络和估值网络的性能,在强化学习阶段并没有与蒙特卡洛树搜索结合在一起。既然策略网络和估值网络与蒙特卡洛树搜索结合后可以表现出更强的下棋能力,为什么不在强化学习阶段就将蒙特卡洛树搜索结合进来呢?AlphaGo Zero正是采用了这样的方法。
图2.24给出了AlphaGo Zero中采用的深度强化学习流程。开始时先随机设置策略-估值网络中的参数,作为当前版的策略-估值网络使用。复制两套系统作为甲乙双方进行对弈,对弈时均结合蒙特卡洛树搜索,获得若干盘对弈结果,作为棋谱保留。用得到的棋谱采用深度强化学习方法对策略-估值网络进行调整训练,得到更新版策略-估值网络。为了测试更新版策略-估值网络的性能,用更新版和当前版策略-估值网络进行若干盘对弈,如果更新版胜率大于给定值ε,则接受更新版,用更新版代替当前版策略-估值网络,否则保留当前版策略-估值网络,甲乙双方再次进行对弈。重复以上过程直到达到了一定的更新次数,获得了一个高水平的策略-估值网络为止。
小明:原来AlphaGo Zero是这样进行从零学习的,看起来计算量非常大,需要花费很长时间吧?
艾博士:计算量确实大,AlphaGo团队也一直在改进他们的方法,使得训练更加有效。在比较早期的版本中,采用了176个GPU进行训练,而与李世石比赛的版本用了几台机器和48个TPU(TPU是谷歌公司专门用于深度学习的加速器)。到了AlphaGo Zero其效率有极大提高,只用了一台配备4个TPU的机器就完成了训练,不过用时还是比较长的,虽然训练3天后就可以战胜与李世石比赛的版本了,但是需要训练40天才能赶上与柯洁比赛的版本。这也说明了和柯洁的比赛版本具有更好的性能。
小明:AlphaGo Zero是怎么训练的?采用什么损失函数呢?
艾博士:首先AlphaGo Zero在自我对弈的过程中,要记录下全部棋谱用于强化学习,用这些棋谱当作训练样本,对策略-估值网络进行训练。
策略-估值网络有两个输出,分别用了两个不同的损失函数组合在一起。对于估值网络部分,其输出只有一个收益,用的是误差的平方损失函数,即:
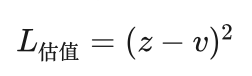
其中z为自我博弈的结果,获胜时为1,失败时为-1;v为估值网络的输出,其值在-1和1之间,v的值要尽可能与z接近。
策略网络部分的损失函数在AlphaGo Zero中又使用了一个小技巧。小明,是否记得在蒙特卡洛树搜索结束后,如何选择一个最佳行棋点?
小明考虑了一下:我印象中是选择选中次数最多的节点作为最佳行棋点。
艾博士赞许地说:对,前面我们解释过这样选择可以使系统性能更稳定。我们刚才说过了,AlphaGo Zero在进行强化学习时,是和蒙特卡洛树搜索紧密结合在一起的,既然搜索结束后是选择选中次数最多的节点为最佳行棋点,那么我们在用BP算法优化时,也可以按照选中次数进行优化。
小明有些不太明白地问:怎么对选中次数进行优化呢?
艾博士解释说:假设s是当前棋局,在完成蒙特卡洛树搜索之后,其每个子节点,也就是在棋局s下所有可能的行棋点,都有一个选中次数,最佳走步就是选中次数最多的子节点。为了优化选中次数,AlphaGo Zero将选中次数转换为概率,并训练策略网络的输出尽可能与该概率一致,从而实现优化选中次数的目的。
小明有些疑惑地问到:具体怎么做的呢?还是不太明白。
艾博士:我们举个例子说明吧。
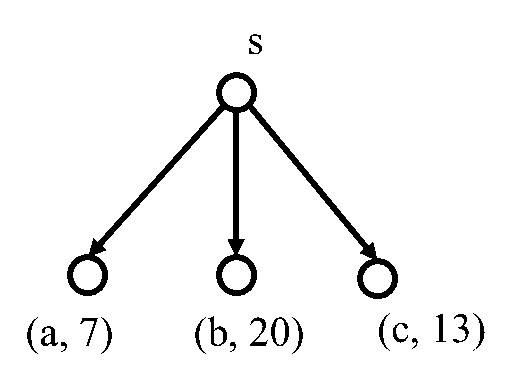
图2.25 选中次数转化为概率示意图
如图2.25所示,假设a、b、c是当前棋局s的3个子节点,在蒙特卡洛树搜索结束时,三个子节点被选中的次数为别为7、20、13,每个节点被选中的概率就是该节点的选中次数除以三个节点选中的总次数。这样a、b、c三个节点的选中概率我们用π表示,分别为:
π(a)=7/(7+20+13)=0.175
π(b)=20/(7+20+13)=0.5
π(c)=13/(7+20+13)=0.325
这3个概率是通过蒙特卡洛树搜索得到的。对于策略网络部分来说,当输入当前棋局s后,对a、b、c三个子节点也会输出概率值,我们记为p(a)、p(b)、p(c)。p(a)、p(b)、p(c)的值应该尽可能与π(a)、π(b)、π(c)的值接近,这是我们的训练目标。为此可以采用交叉熵损失函数达到这一目的,因为交叉熵损失函数可以衡量两个概率分布的差异性。
L=-π(a)log(p(a))-π(b)log(p(b))-π(c)log(p(c))
在AlphaGo Zero中,策略网络部分也采用同样的损失函数。为了表达方便,我们用 πi(i=1,2,...,162) 表示通过蒙特卡洛树搜索得到的当前棋局s的每个子节点的选中概率,之所以共有162个,是因为在19×19的围棋盘上共有161个行棋点,然后将是否放弃行棋也作为一个行棋点对待,所以共有162个。策略网络部分的输出也是162个,分别用 pi(i=1,2,...,162) 表示,这样交叉熵损失函数可以表示为:
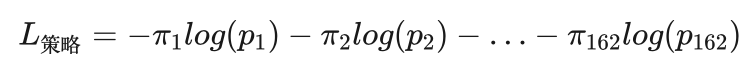
因为在AlphaGo Zero中策略网络和估值网络融合在一起形成了一个神经网络,所以需要将两个网络的损失函数合并在一起,同时为了减少过拟合现象的发生,在损失函数中又增加了一个正则化项,综合以后的损失函数为:
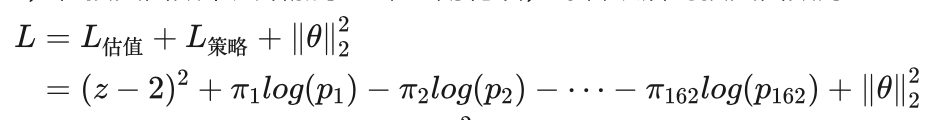
其中θ表示神经网络的所有参数, 是2-范数正则化项。有关过拟合与正则化项的关系,可以参看第一篇《神经网络是如何实现的》相关内容。
小明:谢谢艾博士的讲解,这些内容实际上您之前都讲过,这样综合起来使用,不但了解了AlphaGo Zero是如何从零学习的,也对以前学过的知识有了更深入的理解。
艾博士:是这样的,很多创新都是在已有工作的基础上完成的,所谓站在巨人的肩膀上,做研究一定要对前人的工作有深入的了解,不能闭门造车。
艾博士又继续补充说:通过自我对弈实现从零学习是AlphaGo Zero的最大特点,由于这种学习是完全没有人类指导的随机学习,就像人会迷路一样,可能会走向错误的方向。为了防止这种现象的发生,一种有效的方法就是在蒙特卡洛树搜索过程中,对策略网络得到的概率增加一定的噪声,人为加大某些落子点的行棋概率,探索更多的行棋可能性。
小明问:这样会不会造成学习到一些不太好的走法?
艾博士解释说:不会的。因为如果这些落子点不是一个好的行棋点的话,经过多次蒙特卡洛树搜索的选择之后,其收益会逐步降低,选择过程最终还是会选择那些更好的行棋点,而放弃不好的行棋点。但万一是好的行棋点呢?就会像发现新大陆一样,探索出一片新天地。这也是蒙特卡洛树搜索的特点之一,在多次搜索之后,是有机会摆脱掉那些不好的探索方向的。
小明问:那么如何增加噪声呢?
艾博士回答说:AlphaGo Zero采用了利用狄利克雷分布抽取噪声的方法。狄利克雷分布是一个关于概率分布的概率分布,在参数的控制下,可以产生一些符合一定条件的概率分布。狄利克雷分布有两个参数,一个是向量长度n,即产生的概率分布由多少个元素组成,这n个元素组成的向量构成了狄利克雷分布的抽样结果。由于抽样结果也是一个概率分布,所以应该满足概率分布的一些性质,比如n个元素值之和为1。另一个参数是分布浓度α,当α比较大时,产生的概率分布比较平缓,也就是说n个元素的概率值相差不大,当α比较小时,产生的概率分布具有“突变”性,也就是说n个元素中绝大部分的取值接近于0,但有少量几个元素值比较大。在AlphaGo Zero中,利用α比较小时狄利克雷分布采样的这种性质,通过狄利克雷分布产生一个与策略网络输出同样大小的向量作为噪声,然后在策略网络输出与狄利克雷分布输出之间做加权和,用以代替策略网络的输出。由于这样得到的狄利克雷分布采样的绝大部分元素接近于0,所以策略网络的绝大部分输出并没有受到什么影响,只有哪些个别的处于“突变”点上的概率被人为加大了,这也刚好符合我们对落子概率增加噪声的初衷。
小明:狄利克雷分布,又是一个以前不知道的知识点,看来需要广泛地学习各种知识,以备不时之需。
艾博士:从以上介绍可以看出,AlphaGo Zero将深度学习与蒙特卡洛树搜素巧妙地融合在了一起,神经网络部分也简化成了一个,并在蒙特卡洛树搜索中取消了随机模拟,用估值结果代替。不但性能得到极大的提高,计算量反而降低了,在一台服务器上加4个TPU就可以完成训练。这也是不断磨练,精益求精的结果。
小明读书笔记
AlphaGo Zero完全摆脱了人类数据,实现了从零学习,这不仅体现在训练时不再使用人类棋谱,完全依靠自我对弈产生的数据进行学习,还反应在输入上,由原来的48个通道减少到17个通道,而这17个通道除了一个通道表示黑白方谁走棋外,其他16个通道就是到目前为止的8个棋局,每个棋局用两个通道表示,不需要任何认为构造的特征。另外就是,对于是否需要“放弃”行棋,也作为一个“行棋”来考虑,通过搜索得到,而不是像以前那样依靠程序判断。某种意义上真正做到了从零学习。当然这种从零学习利用了下棋可以自行判断胜负这一特点,并不容易推广到其他的应用方面。
AlphaGo Zero将深度强化学习与蒙特卡洛树搜索融合在一起,在自我对弈时就用到了蒙特卡洛树搜索,这样可以获得质量更好的训练数据。而由于最后选择的是根节点所有子节点中被选择次数最多的子节点作为最佳走步,所以在训练时也是将选择次数转化为概率进行训练,从而策略网络学习追求的目标是被选择次数的最大化。
AlphaGo Zero将策略网络和估值网络合并在一起,组成了一个策略-估值网络。该网路由共用的网络“体”和两个独立的网络“头”组成,网络体部分采用残差网络,然后分开成两个头,分别对应策略网络的输出和估值网络的输出。策略网络的输出为162个,其中161个为可落子点的行棋概率,另一个为放弃行棋的概率,这是AlphaGo Zero特有的一个输出,以判断什么时候就不再下棋了。当对战双方都选择放弃时,对局结束。估值网络的输出只有一个介于-1和1之间的值,是当前棋局收益的估计。
训练采用的损失函数,对于策略网络部分,采用的是交叉熵损失函数,由选择次数转化的概率作为标记,与策略函数的输出计算交叉熵。对于估值网络部分,采用误差的平方作为损失函数,以对局的胜负作为训练目标,与估值网络的输出构成误差的平方。两个损失函数加权平均后作为策略-估值网络的总的损失函数,用BP算法进行统一优化。
由于深度强化学习并不能保证总是沿着正确的方向优化,为此采用了两个策略。一是利用狄利克雷采用,随机地加大策略网络某些输出的概率,以便进行更广泛的探索。二是每训练一个周期后,都要与之前得到的模型进行若干次对弈,以便评判哪个模型更好,只有新模型显著好于旧模型时,新模型才会被接受,并在此基础上继续进行强化学习。
未完待续

