
很多人工智能算法最后会表示成一个组合优化问题,即给定一些限制条件,对某一个目标函数f(x)求最优解,其中x是需要优化的变量。在实际问题中,这一优化问题往往非常复杂,很难直接推导出求解公式。研究人员提出了很多特殊的求解方法,其中遗传算法是很有趣的一种。
众所周知, “物竞天择、适者生存”是达尔文进化理论的基本原则。依这一理论,生物之所以能够不断进化,基本上是靠“试”出来的:种群不断繁衍出新个体,自然选择把优秀的个体留下,把劣质个体淘汰,周而复始,整个种群的质量就一点点提高了。这一自然选择过程不仅使单个种群质量提高,同时也催生了适应环境更强的新物种,演化出了地球上丰富多彩的生物形态,也使物种越来越高级,最终诞生了人类。
图1:生物进化过程[1]

总体来说,生物进化可以归结为三个过程:(1)选择:适应环境者有较大可能性存活下来,不适应者则可能被淘汰;(2)繁殖:父母婚配,繁衍下一代种群;(3)变异:在繁衍过程中,某些基因可能会出现突变。生物进化是这三个过程的往复运行,进化后的种群对环境的适应性越来越好。
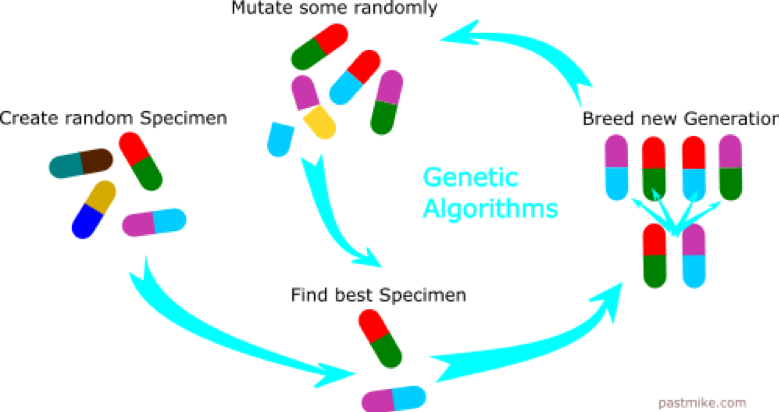
受生物进化过程的启发,美国密歇根大学J. Holland教授提出了一种称为“遗传算法”的优化方法【2】。这一算法的基本思路是随机生成一些新的解,保留那些比较优质的解,去掉那些质量较差的解,这样慢慢提高解的质量。遗传算法的基础流程如图2所示。
图2:遗传算法基本流程[4]。由一个初始种群开始(左),选择优质个体(下), 交叉繁衍新一代种群(右),经过随机变异(上)后进入新一轮选择。
具体来说,如果我们要最大化某个函数f(x),可以将x的不同取值视为生物个体,f(x)视为个体x对环境的适应性,那么对f(x)的优化问题将等价于一个生物进化问题:即通过生物进化过程逐渐改善个体x的适应能力,从而逐步提高f(x)的取值。
更加具体来说,我们首先需要对x进行编码,编码方式有二进制编码、整数编码、二叉树编码等。这有点类似于用DNA来代表个体,DNA即是x的编码。有了这个编码,就可以模拟生物进化的三个过程来对个体x进行优化了。这三个过程分别是:
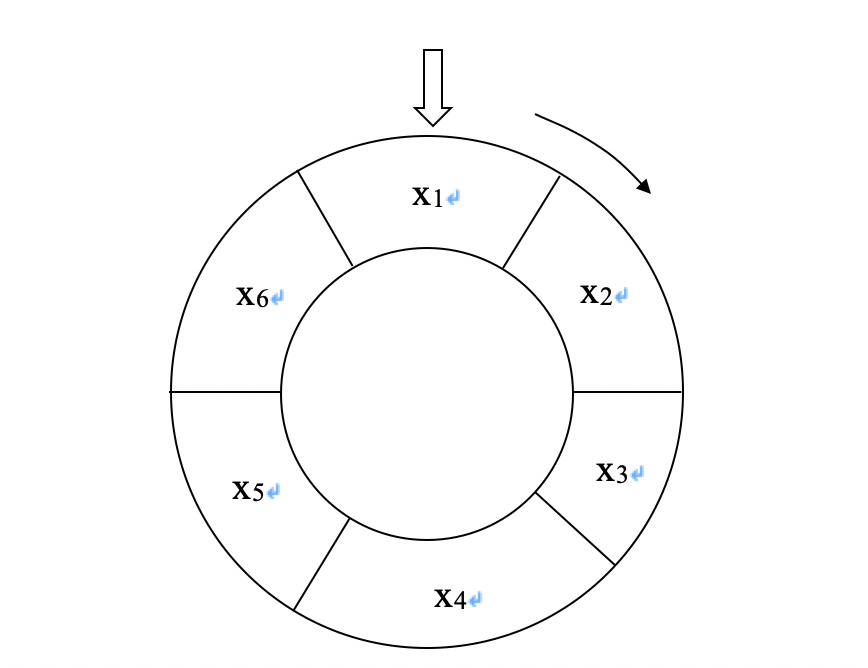
1.选择:按照概率对群体中的个体进行优胜劣汰的选择,选中者进入下一代种群,否则被淘汰。常用的选择方法是“轮盘赌”(如图3所示)。在这一方法中,选择个体x的概率与该个体的适应函数f(x)成正比。这样,适应函数值较大的个体被选择的概率更大。
图3:基于适应函数f(x)的个体选择
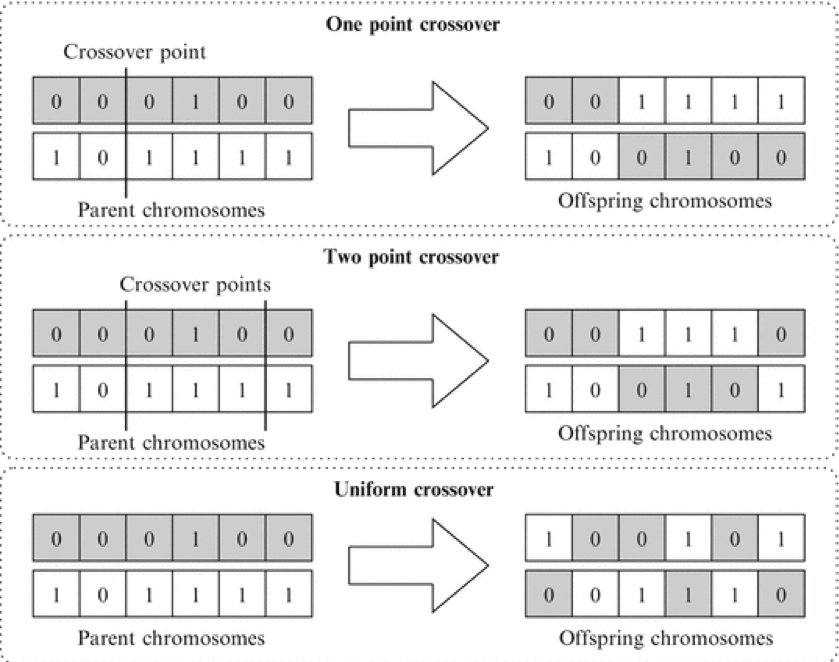
2.交叉:类比于生物进化中的繁殖过程,由父母两个个体的DNA交换片段产生后代。当使用二进制编码时,每个个体的DNA表示为一个0/1串,交叉操作如图4所示。
图4:遗传算法中的交叉操作[3]
3.变异:类比于生物进化中的变异过程,DNA中某一位或某几位的取值发生随机改变。在二进制编码情况下,这一操作将某一位的取值由1变成0或者由0变成1。
遗传算法从一个随机产生的群体(x的一些取值)开始,反复应用上述三种操作,一代代遗传下去,直到繁衍到一定的代数为止。遗传算法属于随机算法,每次运行得到的结果都不一样。如果参数选择合理且繁衍的代数足够多,遗传算法得到最优解的概率趋近为1,意思是几乎肯定可以得到最优解[5]。
遗传算法通过不断尝试来优化目标函数,通常效率比较低,然而,它的优势在于可以优化任何形式的函数f(x),特别是很复杂的函数或不连续的函数。从这个角度看,遗传算法是一种通用的优化方法,在人工智能领域有广泛应用。
参考文献:
[1].https://labs.sogeti.com/natures-evolutionary-intelligence-genetic-algorithms-and-its-practical-applications/biological-evolution/
[2].Holland JH (1992) Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. MIT Press
[3].Sastry K., Goldberg D.E., Kendall G. (2014) Genetic Algorithms. In: Burke E., Kendall G. (eds) Search Methodologies.
[4].What is a genetic algorithm? https://pastmike.com/what-is-a-genetic-algorithm/
[5].Eiben A E, Aarts E H L, Van Hee K M. Global convergence of genetic algorithms: A Markov chain analysis[C]//International Conference on Parallel Problem Solving from Nature. Springer, Berlin, Heidelberg, 1990: 3-12.
