1997年IBM公司研制的深蓝首次在正式比赛中战胜国际象棋大师卡斯帕罗夫,轰动了世界。这次胜利背后的一大功臣是大名鼎鼎的α-β剪枝算法,该算法的基本思路是选择一条即使对方做出了最佳应对,己方依然可以得到最大获胜概率的走棋路径,从而在对战中保持走棋优势。
然而,在国际象棋中奏效的α-β剪枝算法在计算机围棋中却没有得到同样惊艳的效果,这是为什么呢?一个重要原因在于α-β剪枝算法严重依赖于对局面评估的准确性,不幸的是,对围棋的局面评估比国际象棋困难的多,不准确的局面评估限制了α-β剪枝算法的性能发挥。
图1:围棋有更复杂的搜索空间,且对局面的评估更加困难

2006年,Rémi Coulom提出了蒙特卡洛树搜索并将其应用于围棋程序中[1],极大提高了计算机围棋的水平,使之拥有了业余高手的棋力,并为AlphaGo最终战胜人类顶尖棋手[2]奠定了基础。那么,这个神奇的蒙特卡洛树搜索到底是个什么东西呢?
1. 蒙特卡洛树搜索
总体而言,蒙特卡树(MCT)搜索算法通过大量随机模拟走棋过程来评估局面,并依评估结果决定走棋位置。更具体来说,基于当前棋局,对每种可能的落子形成的新棋局进行评估,进而选择己方优势最大的落子。如何对每种可能的新棋局进行评估呢?最简单的方法是考虑所有可能的后续落子方式,并依这些走法的最终胜负进行综合打分。但在围棋里不同走法实在太多了,把他们全部模拟出来是不可能的。蒙特卡树搜索采用一种随机模拟的方法,在计算量可控的前提下尽量模拟那些收益最大的走棋方式。
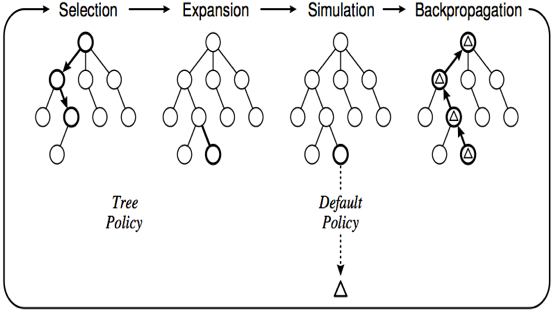
图2给出蒙特卡树搜索算法的一次模拟采样过程所包括四个步骤:
1, 选择(Selection):以当前棋局作为根节点,按照某种路径选择策略(Tree Policy)自上而下依次选择节点,直到遇到第一个存在未扩展子节点的节点A(即A还有未扩展出来的子节点)。
2, 扩展(Expansion):生成A的子节点B,相当于在A所对应的棋局状态下走了一步棋,得到节点B对应的棋局状态。
3, 模拟(Simulation):对B节点进行采样模拟,即按照缺省走棋规则(Default Policy)随机地一步一步下棋,直到决出胜负。该胜负值作为B节点此次模拟获得的收益。
4, 回传(Backpropagation):对B的一次模拟也是对其父节点A以及A的所有祖先的模拟,所以B获得的收益要逐层上传,直到到达根节点。
反复重复上述过程,树中每个节点累积的收益将代表该节点所对应的棋局的己方胜率。当模拟完成后,根结点中收益最大的子节点所对应的走棋方式即为最优落子。
图2:蒙特卡洛树(MCT)搜索算法的四个步骤
2. 基于信心上限决策的路径选择
蒙特卡洛树搜索过程有点类似于人类下棋时的计算过程,搜索树的深度相当于向前看多少步棋,对棋局的判断则是通过多次“模拟”这个走棋过程实现的。人在计算的过程中,对可能的走棋点会分轻重缓急,重要的点多考虑,次要的点少考虑,甚至不考虑。通过在蒙特卡树搜索算法的“选择”步骤中引入信心上限决策,可以实现类似的重点节点选择。
信心上限决策是研究多臂老虎机问题时提出的一个统计决策模型,该问题的设计如下:多臂老虎机拥有K个手臂,拉动每个手臂所获得的收益遵循一定的概率分布且互相独立;要解决的问题是如何找到一个策略,依这一策略每次选择拉动一个手臂,使得最终获得的整体收益最大化。在围棋问题中,每个落子点相当于多臂老虎机的一个臂,拉动哪个手臂相当于对相应节点进行选择。信心上限决策方法在选择节点时会考虑两个因素:
1,实用性(Exploitation):优先选择到目前为止胜率最大的节点,以保证搜索的质量。
2,探索性(Exploration):优先选择到目前为止模拟次数比较少的节点,以保证搜索的增覆盖度。
信心上限决策方法选择Ij最大的节点,其中Ij是上述两个因素的加权和,计算如下:
其中,Xj是节点j目前的收益(即获胜概率),n是到目前为止总的模拟次数,Tj(n)是节点j目前的模拟次数,C是加权系数,对二者的重要性进行调节。
3.AlphaGo
图3:AlphaGo中的神经网络和蒙特卡树搜索[3]
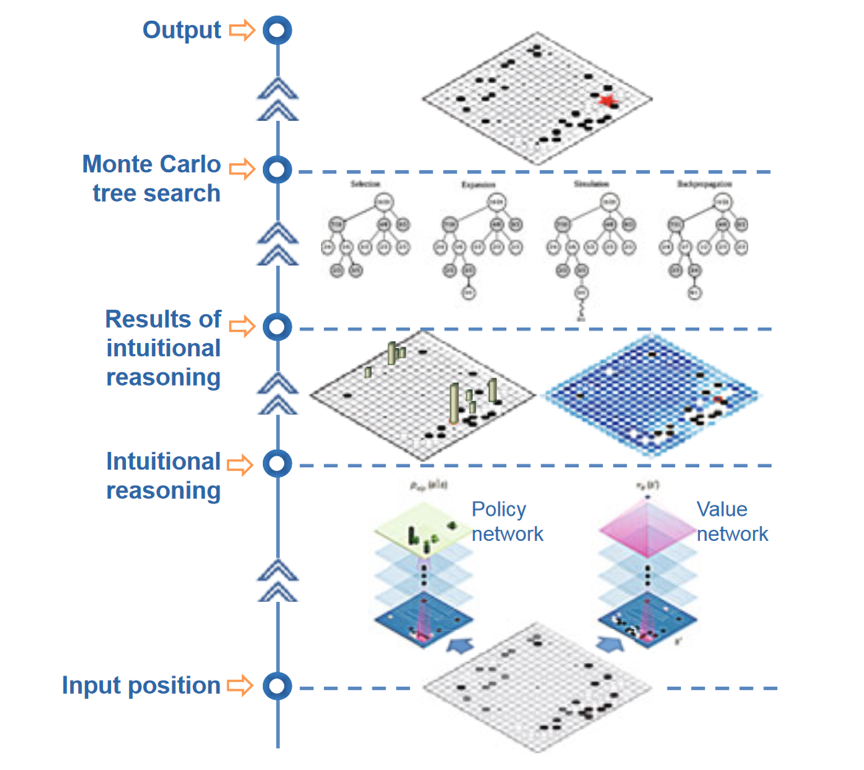
蒙特卡洛树搜索极大提高了计算机围棋的水平,但并没能占胜人类顶尖棋手。一个原因是在模拟的过程中没有引入任何启发信息,完全是随机的模拟。由于围棋的状态空间巨大,模拟次数相地来说严重不足,从而影响了模拟的准确性,限制了计算机围棋水平的提高。
AlphaGo将深度学习方法引入到蒙特卡洛树搜索中,主要设计了两个深度学习网络,一个为策略网络,用于评估可能的落子点;另一个为估值网络,可以对给定棋局的胜负进行估值。AlphaGo将这些信息融合到盘面估值、节点选择和模拟走棋过程中,实现了更高效的搜索和更准确的估值,从而进一步提高了围棋程序的棋力。在训练过程中,AlphaGo学习了人类3000万步走棋,还把增强学习和自我对弈引入到模型训练中,有效提高了深度神经网络模型的精度。
最后,AlphaGo集成了强大的计算能力,征用了一个由1920 个 CPU 和 280 个 GPU 组成的分布式计算系统。这一强大的算力使得AlaphGo在做蒙特卡树搜索时可以模拟更多棋局,对盘面的估值也更精确。
总结起来,AlphaGo综合了蒙特卡洛树搜索和深度神经网络的优势,并利用了强大的计算能力,最终战胜了人类最高水平的棋手。
参考文献:
[1] Coulom R. Efficient selectivity and backup operators in Monte-Carlo tree search[C]//International conference on computers and games. Springer, Berlin, Heidelberg, 2006: 72-83.
[2] Silver, David; Huang, Aja; Maddison, Chris J.; Guez, Arthur; Sifre, Laurent; Driessche, George van den; Schrittwieser, Julian; Antonoglou, Ioannis; Panneershelvam, Veda. Mastering the game of Go with deep neural networks and tree search. Nature: 484–489. [2016-01-31].
Zheng;, Nanning & Liu, Ziyi & Ren, Pengju & Ma, Yongqiang & Chen, Shitao & Yu, Siyu & Xue, Jianru & Chen, BD & Wang, Feiyue. (2017). Hybrid-augmented intelligence: collaboration and cognition. Frontiers of Information Technology & Electronic Engineering. 18. 153-179.
