近年来人工智能领域最火爆的词无疑是“深度学习”了。所谓深度学习,可以简单理解为基于深度神经网络的学习。那么什么是深度神经网络呢?
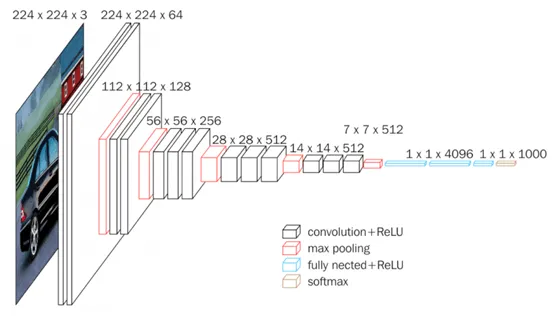
最直接的理解是,深度神经网络(Deep Neural Network, DNN)是层数超过三层的神经网络。例如,用于图像识别的VGGNet层数达到19层[1],而ResNet达到152层。
图1:用于图像识别的VGGNet-16网络架构[1]
把神经网络变深有什么用呢?最直观的好处是深度网络具有更强的表达能力,用同样个数的神经元可以实现更复杂的功能。人们很早就发现了这一点,但一直没有引起足够的重视。这不得不从神经网络的一个重要定理讲起。
早在上个世纪80年代, George Cybenko 等人就发现[3],如果选择合理的激发函数且隐藏层的节点数足够多的话,一个三层的神经网络可以逼近任何连续函数,这一结论称为通用近似定理(Universal approximation theorem)。这意味着一个三层网络就可以包打天下了,既然如此,为什么还要费力去设计更深层的网络呢?大不了多用些神经元就是了。
另一个原因是人们在实验中并没有发现深度网络有更好的效果。事实上从Hinton等人提出反向传播(BP)算法以来,深度网络的训练就没有了理论上的障碍:不论多少层的网络,BP算法都可以训练出来。于是就有人尝试用BP算法来训练三层以上的网络,但大多数实验效果都一般,慢慢的人们也就失去了兴趣。
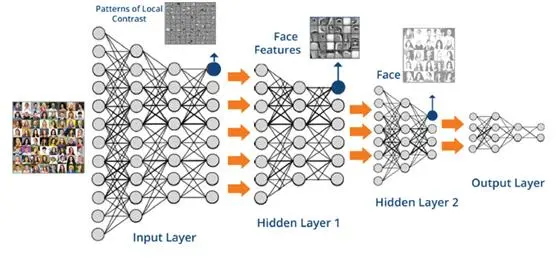
革命性的变革发生在2006年,Geoffrey Hinton 在Science上发表了一篇文章[2],提出了一种预训练方法来训练多层神经网络。他首先利用一种叫RBM的生成模型来提取数据中的显著特征,并将得到的特征送入另一个RBM,提取更高级的特征。这样一层层学下去,就得到了一个深度神经网络的“原型”,层次越深,学习到的特征就越高级。以人脸图片为例(图2),在较低层次学到的特征可能只是一些简单的线条,再深一层可能学到口鼻等构件的模样,再深层会学到人脸的大致轮廓,等等。有了这个原型网络,再结合人脸识别这一目标任务进行微调(称为Fine Tuning),即可得到非常强大的人脸识别模型。
图2:用于人脸图像处理的深度神经网络
Hinton的工作打开了一扇大门,让人们看到了层次性特征的重要性。在传统观念中,神经网络只是函数拟合的工具,人们用它来构造各种分类器或预测模型,但忽视了不同层次神经元所代表的特征应该是有层次性差异的。Hinton用RBM将这些特征学习出来,并置于神经网络的不同层次,从而显著提高了网络的表达能力。事实上,这种多层特征学习的思路和人的神经系统具有共通之处,我们的听觉、视觉等感知过程就是通过逐层处理,由浅入深地完成感知任务的。从这一角度看,深度神经网络不应该简单地视为浅层网络的技术性扩展,而是一种观念上的革命。正因为如此,很多学者将基于深度神经网络的学习方法称为“表示学习”。
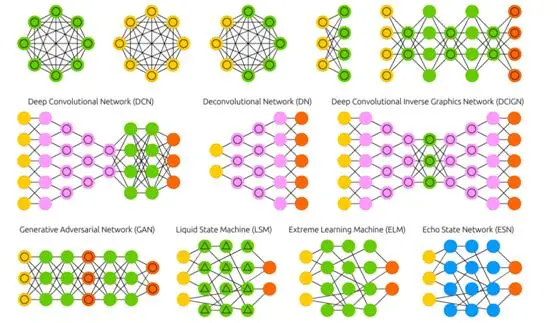
大门打开了,人们的思路也就打开了。从此以后,研究者从各个角度对深度神经网络展开了全方位探索,提出了各种高效的训练方法和各种复杂的网络结构,在语音信号处理、图像视频处理、自然语言处理等众多领域取得了巨大成功。
图3:各种神经网络变种[4]
今天深度学习的进展也许已经远远超出了Hinton在撰写那篇Science论文时所能想象的边界,甚至他当初提出的预训练方法在很大程度上已经不必要了。人们逐渐认识到,“深度”本身也许并不是最重要的事情,更重要的是当前海量的数据积累所提供的资源优势使得基于学习的人工智能方法更加强大,而复杂神经网络模型正是目前已知最高效的学习模型。从这个意义上说,深度学习事实上是大数据学习时代到来的第一声号角。这是一个崭新的时代,数据和学习无疑是这个时代的主角。通过从海量数据中学习知识和规律,机器可能获得远超人类的技能,从而极大扩展了机器智能的边界,而Hinton在2006年的那篇论文无疑具有划时代的意义:没有那篇文章带来的信心,人们恐怕还无法想象当复杂网络和海量数据相结合后所带来的翻天覆地的变化。
十几年过去了,深度学习的发展依然生机勃勃。同时,人们也开始意识到单纯从数据中学习带来的风险,数据的代表性问题,模型的可解释性问题,可持续学习问题,领域泛化问题等都还没有得到很好解决。一些新的方法开始出现,包括结合知识的学习和推理方法,基于因果关系的模型框架等等。可以想见,未来二十年机器学习领域将更加风起云涌,在改变我们生活方式的同时给我们的世界观带来更加深刻的变革。
参考文献:
[1]. Karen Simonyan, Andrew Zisserman, Very Deep Convolutional Networks for Large-Scale Image Recognition, https://arxiv.org/abs/1409.1556
[2]. Hinton, G. E. and Salakhutdinov, R. R. (2006) Reducing the dimensionality of data with neural networks. Science, Vol. 313. no. 5786, pp. 504 - 507, 28 July 2006.
[3].Cybenko,G(1989)"Approximationbysuperpositionsofasigmoidal function", Mathematics of Control, Signals, and Systems, 2(4), 303–314.
[4].TheNeuralNetworkZoo,https://www.asimovinstitute.org/neural-network-zoo/
