第三篇 计算机是如何找到最优路径的(一)
清华大学计算机系 马少平
艾博士导读
最优路径问题是人工智能研究中的一个重要问题,很多问题都可以转化为最优路径求解问题,如语音识别、汉字识别后处理、拼音输入法等。
A*算法是求解最优路径的一个重要算法,在人工智能中具有重要地位,曾经被列为计算机领域最重要的32个算法之一。
那么都有哪些最优路径搜索算法呢?这些算法各自的特点是什么?每种算法是否可以找到最优路径?或者在什么条件下可以找到最优路径?本篇将逐一介绍,解开这些谜团。
本篇内容按照难易程度划分为三个等级,读者可以根据自身需要有选择的读其中几节或者全部内容。
第一级:3.1、3.2节、3.3节和3.5节。介绍什么是最优路径问题,然后通过一个实际例子,引出了宽度优先搜索算法,介绍宽度优先搜索算法具体过程,有哪些性质,以及存在的不足。在此基础上,引出迪杰斯特拉算法,介绍该算法的求解过程以及所具有的性质,并分析该算法存在的不足。介绍什么是深度优先搜索算法及其性质。
第二级:3.4节。针对迪杰斯特拉算法的不足,引入启发函数的概念,给出了A算法,介绍A算法的求解过程。然后通过对启发函数加以必要的限制,引出A*算法,介绍A*算法的性质,介绍如何设计启发函数的基本思路,并给出几个具体例子。介绍如何评价两个不同的启发函数的方法。针对A*算法存在的问题,引出单调启发函数的概念,分析单调启发函数的性质。最后介绍如何克服A*算法存在的不足,提出改进的A*算法。
第三级:3.6节到3.8节。针对宽度优先搜索算法、A*算法存在的占用空间过大的问题,提出迭代加深式搜索的概念,利用深度优先搜索占用空间比较小的优势,与宽度优先搜索算法、A*算法相结合,提出迭代加深式宽度优先搜索算法、迭代加深式A*算法,实现在占用较小空间的情况下求解最优路径问题。介绍一种常用的动态规划算法Viterbi算法,介绍算法适用的问题和实现的基本原理。最后通过一个拼音输入法问题实例,介绍如何将该问题转换为一个最优路径问题,并给出用Viterbi算法求解拼音输入法问题的方法。
秋天到了,正是看红叶的季节。北京香山的红叶最为著名,小明计划周末和同学们一起骑车去香山看红叶。小明虽然以前多次和父母去过香山,但是每次都是爸爸开车去的,小明并不熟悉如何到达香山。不过这也难不倒小明,手机上有导航软件,输入目的地香山后,很容易就可以找到到达香山的路线。现在的导航软件做的是真好,可以提供好几条路线供选择:有距离最短,有花费时间最短,还有经过的红绿灯最少等,给出的是不同条件下的最优路径。这引起了小明强烈的好奇心:计算机是如何找到最优路径的呢?
游玩香山回来之后,带着这个问题,小明又来找艾博士请教。
图3.1 从清华大学到香山公园路线
第一节:路径搜索问题
明白了小明的来意之后,艾博士从书柜里找出了一张很久未用的纸质地图。
艾博士指着地图对小明说:现在真是太方便了,无论想去哪里,导航软件都能很快给出路径出来。以前我们都是依靠这种地图,在地图上查找半天,才能找到一条合适的路线。
艾博士让小明尝试着找到一条去香山的路。小明由于是第一次使用这种纸质地图,在地图上探索半天,才好不容易找到了一条到达香山的路线。
艾博士问小明:小明,你刚才是怎么找到去香山的路线的呢?
小明回答说:刚开始我有些不得要领,完全是无规律地乱找。后来我发现主要是找路口,重要的是在哪个路口应该向哪个方向走,因为相邻的两个路口之间只有一条路,是不需要考虑如何走的。
艾博士夸奖到:小明你真聪明!其实所谓的路线,就是将经过的路口——包括道路的入口和出口——连接在一起。所以找路线,重要的就是找到这些必须经过的路口。
为此,我们可以将路口看做是一个状态,相邻的路口用称作“边”的连线连接在一起,这样地图就可以用这种状态连接图表示了。如图3.2所示,就表示了一个简单的地图,图中A、B、C等表示的是路口,两个相邻路口用边连接在一起。边旁边的数字表示两个路口之间的距离。比如S到A的距离为6。这里的状态,在图中又称作是节点。
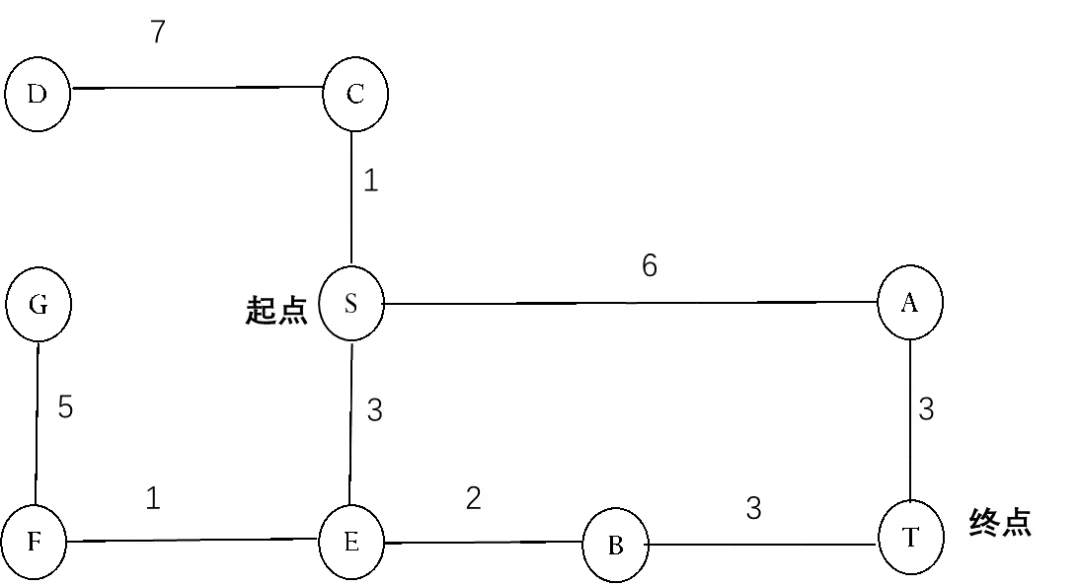
图3.2 状态连接图示意
艾博士总结说:在地图上找出从起始地点S到目标地点T的路线,就是在这样的状态连接图上寻找出几个状态,这些状态连接在一起,可以从起始点S到达目标地点T。这就是路径搜索问题。如果找到的路径满足一定的最优条件,则是最优路径搜索问题。由于这种搜索是在状态连接图上进行的,所以又可以称为状态搜索问题。
小明着急地问到:艾博士,那么如何通过状态连接图搜索到路径呢?
艾博士:小明,我们先不着急介绍具体的搜索算法,先来看看这里的关键问题是什么。以图3.2为例,假设S是所在的起点,T是要去的终点。从S出发可以到达A、C、E,我们用图3.3所示的搜索图表示。图中由于A、C、E三个节点是从S生成出来的,所以这三个节点称作是S的子节点,S称作这几个节点的父节点。父节点产生子节点的过程称作扩展。
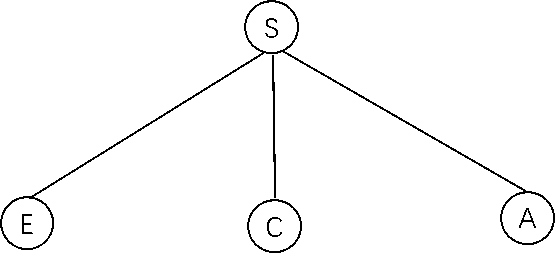
图3.3 从S扩展出三个子节点A、C、E
由于连接S的只有A、C、E这三个路口,所以要到达目标T的话,必须经过这三个路口中的一个,那么下一步应该选择哪个节点扩展呢?假设选择了节点E扩展,则生成子节点B和F,得到的搜索树如图3.4所示。
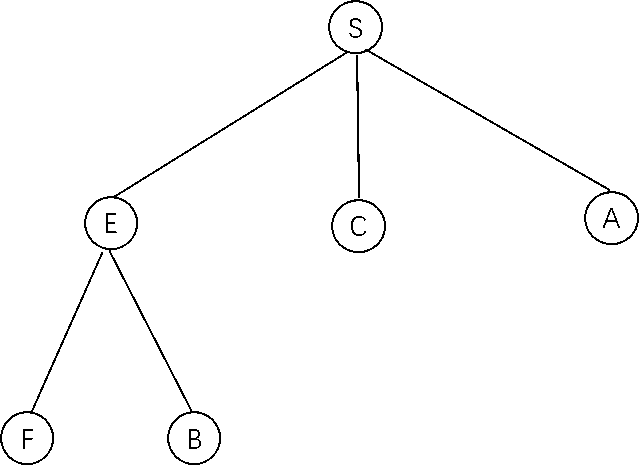
图3.4 扩展节点E生成出子节点B、F
到这一步之后,又面临选择哪个节点扩展的问题,从可能经过的A、B、C、F四个路口中选择一个节点扩展。
讲到这里,艾博士问小明:小明,你说说看,这里的关键问题是什么?
小明想了想回答到:这里的关键问题应该是如何选择哪个节点优先扩展。
听了小明的回答,艾博士非常高兴:小明,你说的很对。如何选择节点优先扩展是状态搜索问题的关键所在。事实上,不同的选择方法,就构成了不同的搜索算法。不同的算法具有不同的性质,下面我们分别介绍几个常用的方法。
另外我们需要强调的是,通过状态搜索不只是可以求解路径问题,很多问题都可以转化为状态搜索问题进行求解。比如八数码问题。
小明不解地问:八数码问题是个什么问题呢?
艾博士解释说:八数码问题是一个智力游戏问题。在3×3组成的九宫格棋盘上,摆有八个将牌,每一个将牌都刻有1—8数码中的某一个数码。棋盘中留有一个空格,允许其周围的某一个将牌向空格移动,这样通过移动将牌就可以不断改变将牌的布局。这种游戏求解的问题是:给定一种初始的将牌布局(初始状态)和一个目标布局(目标状态),问如何通过移动将牌,实现从初始状态到达目标状态的转变。图3.5给出了一个八数码问题的示意图。
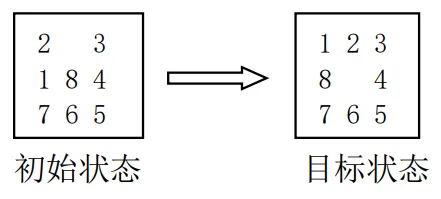
图 3.5 八数码问题示例
小明:我明白什么是八数码问题了,但是这与路径搜索问题有什么关系呢?
艾博士解释说:这个问题实际上跟路径搜索问题是一样的。初始状态可以认为是出发点,在这个状态下走一个将牌形成的新状态可以看做是与初始状态相邻的“路口”。八数码问题的解就是找到若干个相邻的“路口”(状态),可以从初始状态一步步达到目标状态。
小明恍然大悟到:经您这么一解释,八数码问题还真是和路径搜索问题是一样的。
艾博士:还有定理证明问题,从搜索的角度来说,也可以认为是寻找路径的过程。
小明:定理证明也跟路径搜索问题有关?
艾博士:你们正在学习几何吧?几何证明题一般是怎么描述的?又是怎么证明的?
小明想了想回答说:一般都是先给几个已知条件,然后要求证明某个结论,比如证明两条直线平行、两个角相等等。证明过程一般是用某个定理,从已知条件推理出某个结论,然后再反复运用已知的定理得出更多的结论,直到最终得出了要求证明的结论。
艾博士:这里的已知条件就相当于路径搜索问题中的起始状态,而要证明的结论就相当于目标状态。运用定理推导出的一些中间结果可以认为是搜索过程中出现的中间状态,从一个状态推导出另一个状态所用的定理,就相当于连接两个状态的边。所以从搜索的角度描述定理证明的话,就是找到一条从初始条件出发,通过一系列定理连接的、到达要证明的结论的路径。
小明认真思考后说:仔细想想还真是这么一回事。
艾博士:很多问题都可以转化为路径搜索问题,在下面的讲解中,除非特殊说明,我们均以状态连接图上的路径搜索为例做介绍。
小明读书笔记
路径搜索问题就是在一个状态搜索图上,如何选择被扩展的节点,不同的选择方法就构成了不同的搜索算法。
路径搜索方法不仅适用于求解地图上查找路线问题,这里的“路径”是广义的路径概念,很多问题可以转化为路径搜索问题来求解。
未完待续

