
什么是人工智能?从实现的角度现有人工智能可以刻画为“描述+算法”,所谓的描述就是用某种方式告诉计算机求解什么,而算法则是依靠描述将智能问题转化为计算问题,通过计算实现智能。比如现在热门的深度学习就是用数据通过“举例”的方式描述问题,而算法就是深度学习相关的模型和算法,如反向传播算法(BP)等。这里的算法就完全是数学问题。
举例来说,现实问题中绝大多数的推理都具有不确定性,不确定推理问题是构建专家系统的重要问题之一。比如“如果阴天则可能下雨”、“如果湿度大则可能下雨”是两条与下雨有关的规则,这里不仅“阴天”、“湿度”具有不确定性,这两条规则本身也具有不确定性,这么多不确定的内容组合在一起,如何确定是否下雨的可能性呢?这就是不确定推理问题,涉及概率、可能性理论等数学问题,需要用数学来解决。
专家系统
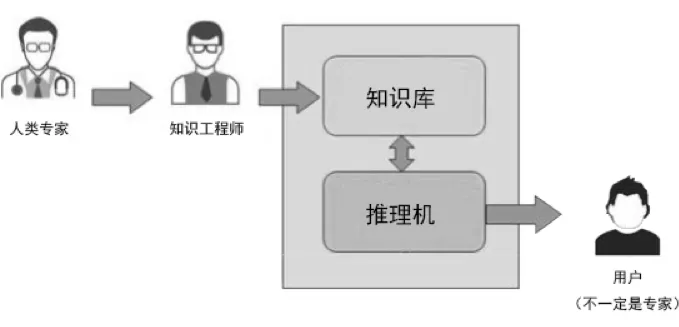
图片来源于网络侵删
九十年代发展起来的统计机器学习方法,对推动人工智能走向应用起到了很大的作用。而统计机器学习的背后则完全依靠数学的支撑。其中最具代表性的支持向量机方法,涉及求解具有不等式约束的最优化问题,要用到拉格朗日乘子法求解,这种方法本身就是数学的产物。但是即便有了拉格朗日乘子法这个数学工具,当数据量大时还是难于求解,直到以序列最小最优化(SMO)算法为代表的快速算法的出现,才使得支持向量机方法得到广泛的应用。无疑快速算法的背后还是数学。
现在最热门的深度学习是在人工神经元网络方法的基础上发展而来,由于曾被认为不存在一种通用的学习算法而被打入冷宫几十年,直到“反向传播算法(BP)”的出现,才重新回到“人间”,又经过二十几年的发展,才有了今天的辉煌,这其中涉及到线性代数、微积分等很多数学的内容。目前深度学习还属于“黑盒子”,还有很多问题需要探讨,无疑这又需要更多更深的数学。
神经网络

图片来源于网络侵删
黑盒子
图片来源于网络侵删
总之一句话,人工智能的发展离不开数学,要想学好人工智能离不开数学,要想发展人工智能更离不开数学。
