贝叶斯公式在机器学习中占有重要地位,是基于概率的推理方法的基础。例如:如果某个地方发生地震的可能性表示为一个概率P(地震) ,而发生地震时井水发混的可能性表示为概率P(井水发混|地震) 。那么,如果有一天发现井水变混了,有多大的可能性会发生地震呢?贝叶斯公式就是用来计算这个可能性的,记为概率P(地震|井水发混)。
基于概率论的基本原理,这个概率可以计算如下:

地震井水变混地震,井水变混井水变混井水变混地震地震井水变混 地震井水变混地震,井水变混井水变混井水变混地震地震井水变混
这样我们就通过“井水变混”这样一个观测结果得到了会发生地震的概率。上面这个公式就是贝叶斯公式,由英国数学家Thomas Bayes于1763年提出。
图1:英国数学家Thomas Bayes

写的更形式化一些,用变量 Y 和 X 代表“地震”和“井水变混”这两件事,贝叶斯公式写成如下形式:
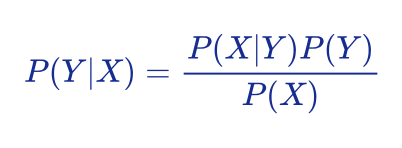
上面公式中,P(Y)是我们没有进行任何观测时对Y发生的可能性的估计,这是我们对 Y 的经验知识,因此称为“先验概率”;P(X|Y) 是当 Y 确定后,观测量 X 的概率分布,因此称为“条件概率”。P(X) 可以理解为在 Y 的所有取值范围内,X 发生的证据。如果 Y 只取0或1,则 P(X) 可以计算如下:
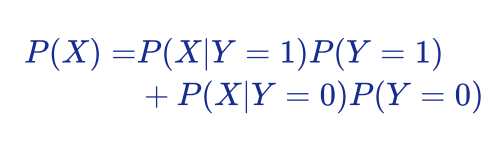
最后,计算的结果 P(Y|X) 表示观察到 X 这一现象后, Y 的发生概率。这个概率和 P(Y) 一样,都是 Y 发生的可能性。不同的是,P(Y) 是没有观察到任何现象时的“先天经验”,而 P(Y|X) 是观察到 X 后对 Y 发生可能性的重新估计。因为这一概率是观察到 X 后得到的,因此称为“后验概率”。很显然,后验概率中包含了新的观察信息,因此更加准确。
贝叶斯公式虽然看起来很简单,但内涵却非常深刻。首先,它将人的经验和观察结果结合起来,得到更符合实际的概率估计。如果我们将经验当成知识,把观察作为数据,贝叶斯公式事实上提供了一种将知识和数据结合起来进行推理的方法,这一方法有坚实的概率基础;第二,如果有更多观察,这些观察可以统一纳入到贝叶斯公式中,提供更多证据,使得对 Y 的概率估计更准确;第三,更多观察数据也可以依次引入贝叶斯公式,将前一次观察得到的后验概率作为后一次估计的先验概率,这样对 Y 的概率估计将随着观察量的累积而越来越准,从而提供了一种逐渐学习的机制。
贝叶斯公式提供的这种推理方法为构造更复杂的概率系统提供了基础工具。基于条件概率,我们可以将成百上千个变量连接起来,形成复杂的概率网络,而贝叶斯公式是在这个网络上进行推理和训练的基础。因此,这一网络也常称为“贝叶斯网络”[1]。
图2:一个贝叶斯网络的例子[2]
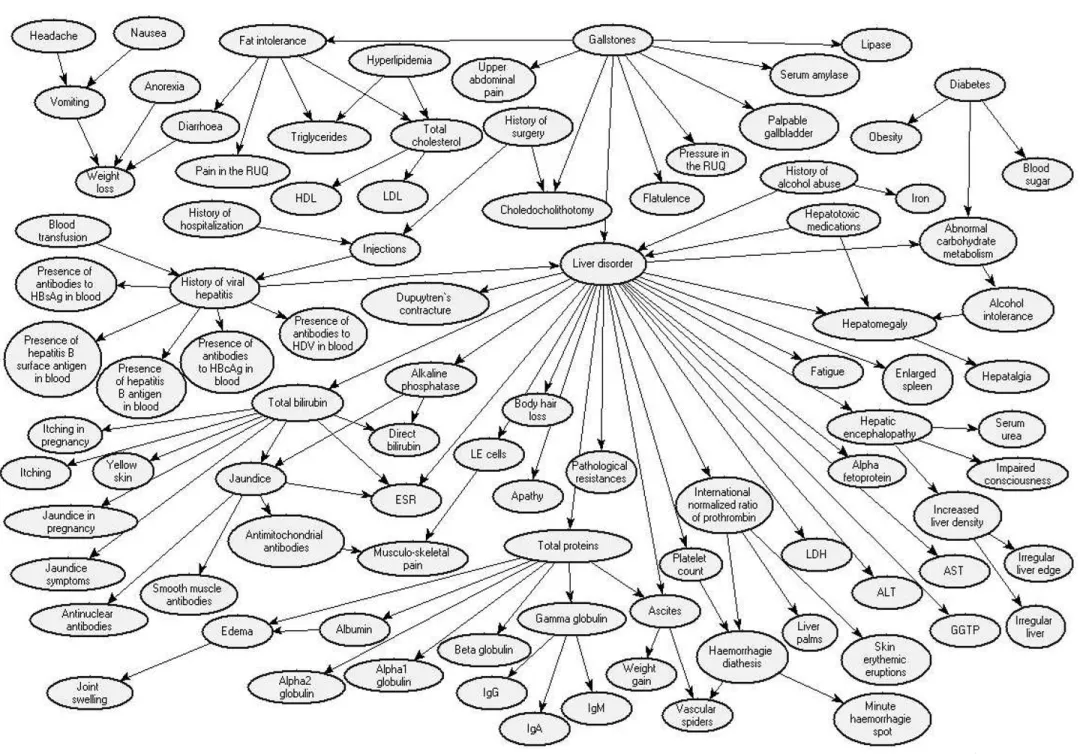
参考文献:
[1] 王东,《机器学习导论》第六章,图模型, 清华大学出版社, 2021.2.
[2] Artificial Intelligence – Bayes Network,https://www.norwegiancreations.com/2018/09/artificial-intelligence-bayes-network/
By:清华大学 王东
