
很多人工智能算法可以归结为对某一函数f(x)的优化任务,其中x为需要优化的变量。模拟退火算法是受金属退火现象的启发而得到的一种函数优化方法。
图1:爬山法可以到达一个山峰,但不能保证到达最高山峰[1]。
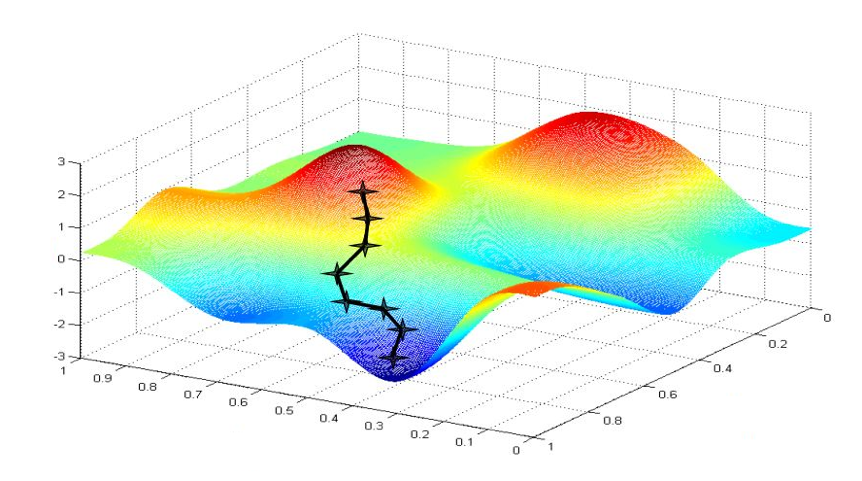
在讨论退火算法之前,我们首先介绍一种称为“爬山法”的优化算法。这一方法将f(x)想象成山的高度,对f(x)的优化过程相当于爬山过程。如图1所示,设想一个在山脚下的盲人,他想要爬上最高峰,问题是他看不到山峰的全局情况,唯一能做的是用手中的拐杖探索自己周围几米的距离,判断哪边高哪边低。为了爬上山顶,他选择了一种方法:每到一个位置,他都用拐杖探索坡起最大的方向,然后试着往这个方向走一步,之后再探索。这样一步一步探索下去,最终总会走到山顶。这一方法称为“爬山法”。
如果只有一个山峰,爬山法必然可以爬到最高峰,对应f(x)最大。但是如果有多个山峰,就未必能爬到最高的那座山峰了,如图1所示。虽然这个小山峰也是不错的,但毕竟和我们想爬到最高峰的目标还有差距。如何解决这一问题呢?计算机科学家们想到了物理学中一种称为“退火”的特殊现象,受此启发设计了一种称为“模拟退火”的算法,取得了很好的效果。
什么是退火呢?比如一根钢丝,被加热到很高的温度后再让它慢慢冷却,冷却后的钢丝将会变得更柔软。其原因是经过这样处理的钢材更趋向于能量平稳状态,从而减少了内部缺陷,这一过程称为退火[4,5]。根据热力学的研究结果,如果钢丝的初始温度足够高,温度下降的足够缓慢,则当温度趋近于绝对0度时,退火后的钢丝将处于能量最低的状态[3]。 退火过程的一个特点是,在温度降低过程中,材料所处的能量并不是持续下降的,而是会以概率跳到一个更高的能量状态,其中T是绝对温度,K>0是波尔兹曼常数,是当前能量与下一状态的能量之差。可以看到,温度越高,越可能跳到一个较高能量状态。
图2:退火过程中,当温度较高时可以跳出能量陷阱;当温度较低时,会约束在当前能量附近[2]。每个小球上面的曲线表示下一次采样时的随机性。可以看到,当温度较高时,小球可以跳出当前能量低谷。
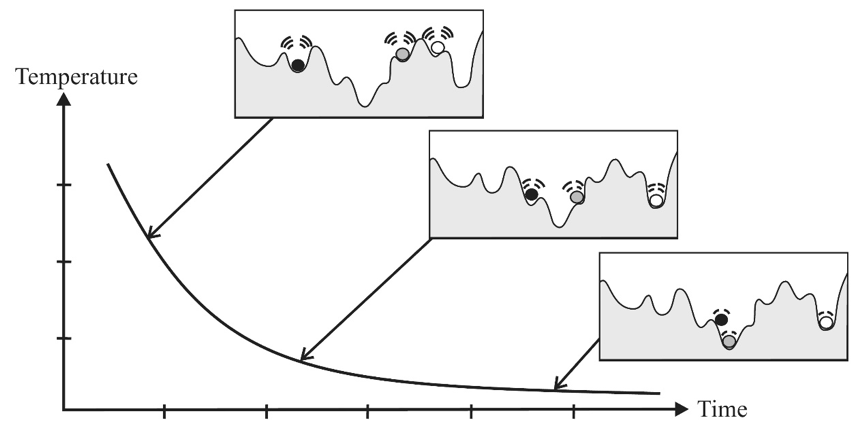
我们利用退火过程来改造爬山法,这种算法被称为模拟退火算法[3]。为说明方便,将爬山改为向低谷搜索,即求目标函数f(x)的最小值。在该算法中,每次搜索不仅向能量更低的方向探索,还保留一定概率向能量较高的方向探索。这样就引入了一个随机性,使得我们可以跳出当前的“能量陷阱”,进入到另一个可能更好的能量低谷中。
具体而言,我们将目标函数f(x)看作是能量函数,用虚拟温度t代替KT。开始时给t一个足够大的值,x取一个随机值作为初始状态。算法首先保持温度t不变,随机的产生一个状态x’。如果该状态的能量f(x’)低于当前能量f(x),即f(x’)<f(x),则接受该状态;如果f(x’)>f(x),并不马上拒绝,而是以概率接受该状态,其中。如果该状态没有被接受,则保持原状态。上述采样过程反复运行,达到稳定后即模拟了金属在温度t下的平稳状态。达到该平稳状态后,我们降低温度t,并在新的温度下重复上述运行过程。不断降低温度t,当t足够低(趋近0)时即得到优化的x。
模拟退火算法属于随机算法,每次的运行结果可能不一样。选择合适的退火方案,则算法将以概率1得到最优解[6]。模拟退火算法和遗传算法有一定相似性,都是通过“尝试“来优化解的质量[7]。不同之处在于,遗传算法是通过群体演化方式寻找最优解,而模拟退火算法通过个体的状态优化寻找最优解。
参考文献:
[1]. Hill Climbing Algorithms (and gradient descent variants) IRL, https://umu.to/blog/2018/06/29/hill-climbing-irl
[2]. Sergio Ledesma, Jose Ruiz and Guadalupe Garcia, Simulated Annealing Evolution, https://www.intechopen.com/books/simulated-annealing-advances-applications-and-hybridizations/simulated-annealing-evolution
[3]. Kirkpatrick, S.; Gelatt Jr, C. D.; Vecchi, M. P. (1983). "Optimization by Simulated Annealing". Science. 220 (4598): 671–680
[4]. Robert E.Reed-Hill、Reza Abbaschian. physical metallurgy principles
[5].https://zh.wikipedia.org/wiki/%E9%80%80%E7%81%AB#cite_note-effrey04-2
[6]. Mitra D, Romeo F, Sangiovanni-Vincentelli A. Convergence and finite-time behavior of simulated annealing[J]. Advances in applied probability, 1986, 18(3): 747-771.
[7]. Eiben A E, Aarts E H L, Van Hee K M. Global convergence of genetic algorithms: A Markov chain analysis[C]//International Conference on Parallel Problem Solving from Nature. Springer, Berlin, Heidelberg, 1990: 3-12.
