主成分分析是一种基础的数据分析算法,常用于数据降维和可视化。我们知道,机器学习中的数据往往是高维的。例如,在描述一个水果时,要考察它的形状、大小、颜色、味道等才能判断它是什么水果,这就至少需要四个维度。
在实际场景中,数据的维度可能更高。维度过高不仅使模型训练变得困难,也难以让我们把握数据分布的整体情况。幸运的是,绝大多数数据处于一个低维空间,意思是只有少数几个维度是关键的。主成分分析的目的就是找到那些最关键的维度。例如,对水果来说,仅仅通过“形状”这一个维度,我们就可以大致判断出它是什么水果。

图1. 基于“形状”一个维度即可判断大部分水果
主成分分析是一种寻找关键维度的常用方法。它的基本思路是在数据空间中画一条线,看数据投影到这条线上后与原始数据的误差是多少。
如下图所示,黑色直线就是我们在数据空间中所画的线,而每个数据点到这条黑线的误差,可以用垂直于这条黑线的红色线段来表示。很显然,当黑色直线旋转到某一方向时,所有投影的误差总和最小。此时,黑色直线的方向就是主成分的方向。从直观上看,这个方向也是数据分散度最大的方向,因此也最能代表数据的整体分布特性。
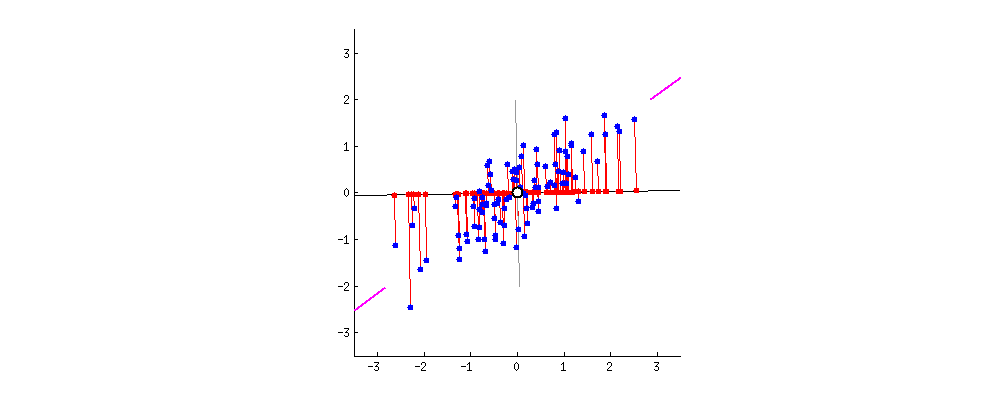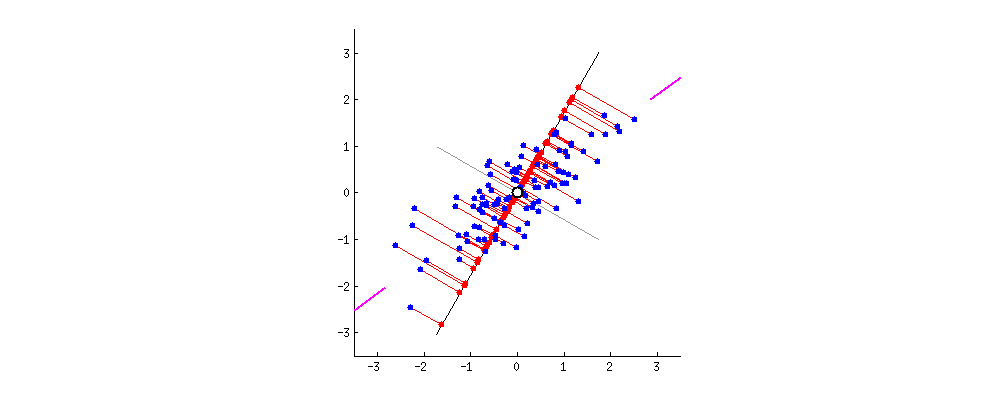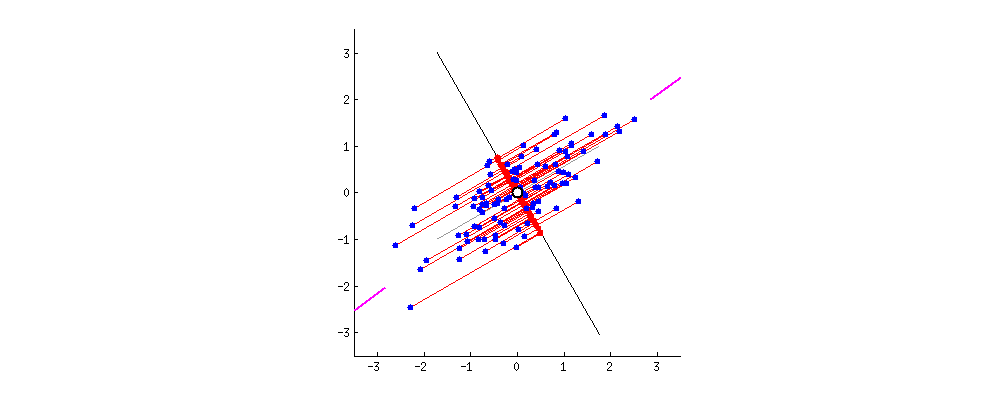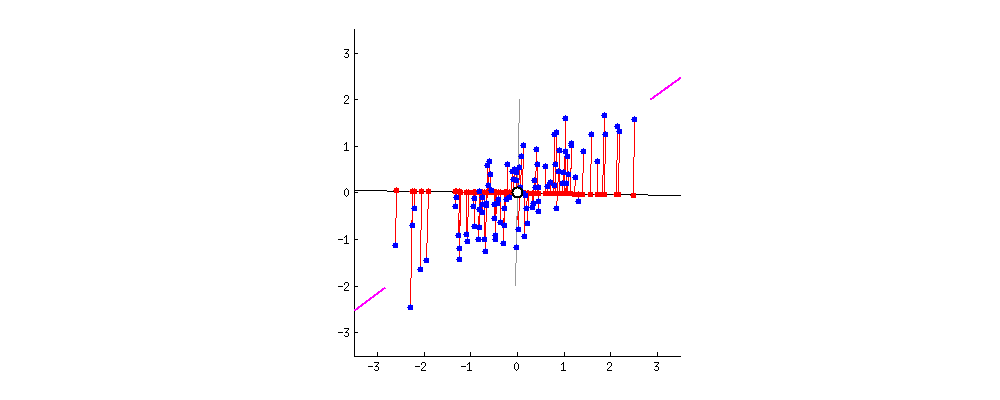
图2. 主成分分析寻找误差最小的投影方向
通过类似的方法,我们可以找到更多的主成分方向,这些方向互相垂直。这就是主成分分析的基本思路。在实际应用时,这些主成分方向可以通过数值计算方法快速得到,而不需要像图中那样对所有方向逐一尝试。
如果我们找到两个主成分方向,就可以在这两个方向定义的平面上呈现数据,从而直观地观察数据的整体分布和不同类别数据之间的关系。这对于理解数据的整体特性、设计相应的学习算法具有重要意义。
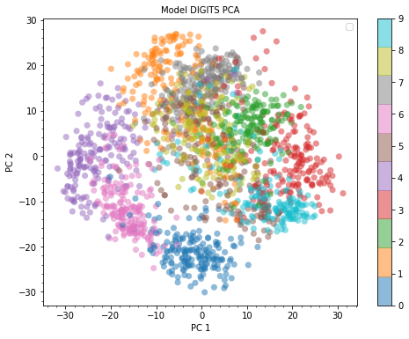
图3. 用主成分分析将数字图片映射到二维空间,实现可视化
供稿:清华大学 王东
制作:北京邮电大学 戴维
审核:北京邮电大学 李蓝天
