所谓维度灾难,从最通常的意义上讲,是指当维度升高时,会产生与低维场景很不相同的现象。这一概念最早由Richard E. Bellman在研究动态规划算法时提出[1]。对机器学习来说,维度升高带来的一个明显“灾难”是数据稀疏。
1. 高维度带来数据稀疏
我们知道,基于统计的机器学习模型要对数据的“真实分布”进行估计,估计的好,模型可以在实用场景得到较好的效果,估计的不好,模型基本就不能用了。这就要求训练数据的密度达到一定程度,才能区分高密度区和低密度区,从而实现对真实分布的合理估计。如果只有三两个数据点,是无法刻画数据分布的真实情况的[2]。
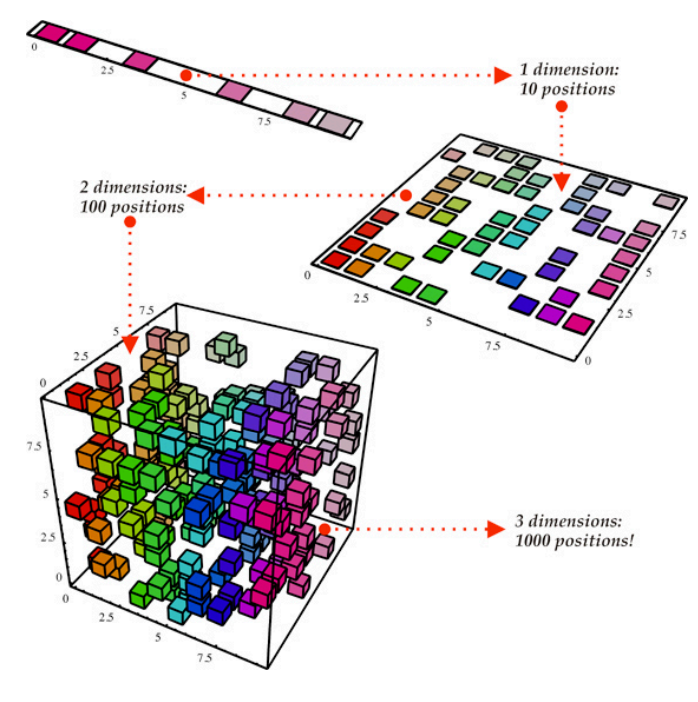
那么问题就来了,要想数据密度达到一定程度,所需要的数据样本个数将随着维度的增加而快速增长。图1给出了一个形象解释:当只有一维时,只有10个位置,为这10个位置估计密度可能用几百个样本就够了;如果升到二维,同样数据范围内就有100个位置了,为这100个位置估计密度,怎么也得上千个样本吧。如果维度再上升,需要估计的位置会呈指数增长,需要的样本点也会越来越多。在实际任务中,我们所能收集到的训练样本数总是有限的,因此过高的维度总会带来模型训练上的困难。
图1:随着维度增加,需要更多数据点以形成合理的密度估计[3]
2. 几点误解
有人会问:维度越高,难度不是信息量越大,带来的性能应该越好吗?这个是没错,但前提是得有足够多的训练数据,这个信息量大的优势才能体现出来。
还有人问:如果我要把特征复制N份,维度提高了N倍,那是不是也要增加数据需求了?答案是不会,虽然复制了N份,但数据是分布在受限空间的,所以密度估计的难度并没有提高。
还有人问:像支持向量机(SVM)这种模型把维度都提高到了无限维,要求的数据量不是无穷大了吗?这个倒不是,看似提高到了无限维,但数据在高维空间中是受核函数限制的,并不会自由分布。
3. 解决办法
因为维度高,所以模型对数据分布估计不准,因此只对训练数据有效,没有可扩展性。因此,维度灾难本质上是过拟合问题。那么,解决过拟合问题的方法就可以用来解决维度灾难了。比如,可以用简单的,不易过拟合的模型(如PCA)选出显著的维度来,再用较复杂的、容易过拟合的模型建模。再比如,可以利用贝叶斯方法,为模型参数引入先验概率,让这些参数不要乱动,也可以解决维度灾难问题。
4. 其它有趣的高维现象
低维空间中习以为常的事情,可能在高维空间中被颠覆。我们来看两个例子。
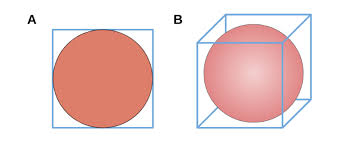
第一个例子是内接球占方框的比例。如图1所示,不论是在二维还是三维空间中,方框的绝大部分体积被内接球占据。如果我们将维度升高,你会发现内接球所占的比例会趋近于零。举个例子,如果你是个木匠,要从一个方木中削出个球,在三维空间中你是幸运的,因为需要削去只是很少一点;如果在高维空间,那就很悲惨,你会发现削去了成百上千吨木头,最后只剩下一个几克的小球。
图2:当维度升高时,内接球的体积占比越来越小
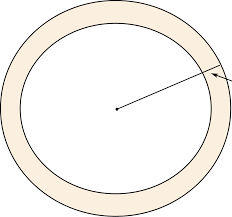
第二个例子是球体积随半径的分布。如图3所示,在二维空间或三维空间中,绝大部分体积会集中在球的内部,但是当维度升高时,绝大部分体积都会集中在球壳附近,维度越高,越向球壳集中。举个剥柚子的例子,在三维空间中你是幸运的,因为你会发现虽然把皮剥了,肉还是蛮多的;如果你剥的是一个高维柚子,那就比较惨烈,你会发现剥掉的皮可能成百上千吨,然后剥完就剩下几克可吃。
图3:当维度升高时,绝大部分体积集中在球壳上
参考文献:
[1]Bellman, Richard Ernest; Rand Corporation (1957). Dynamic programming. Princeton University Press. p. ix. ISBN 978-0-691-07951-6.
[2]王东,“机器学习导论”,清华大学出版社,2021.2.
[3]https://towardsdatascience.com/that-cursing-dimensionality-ac317fb0fdcc?gi=a41bd13bb5da
By:清华大学 王东
