二十年前开车还是靠一张地图走天下,现在如果没有导航几乎是寸步难行了。早期导航还存在一些缺陷,现在的导航还是非常靠谱的,绝大多数情况下不会出错。
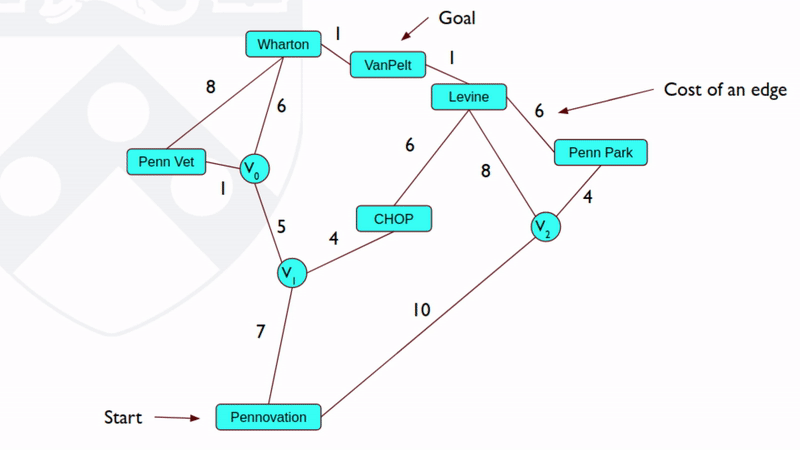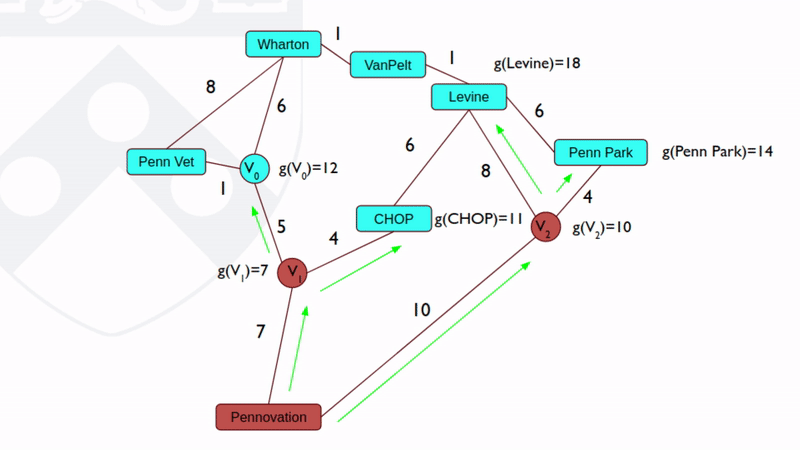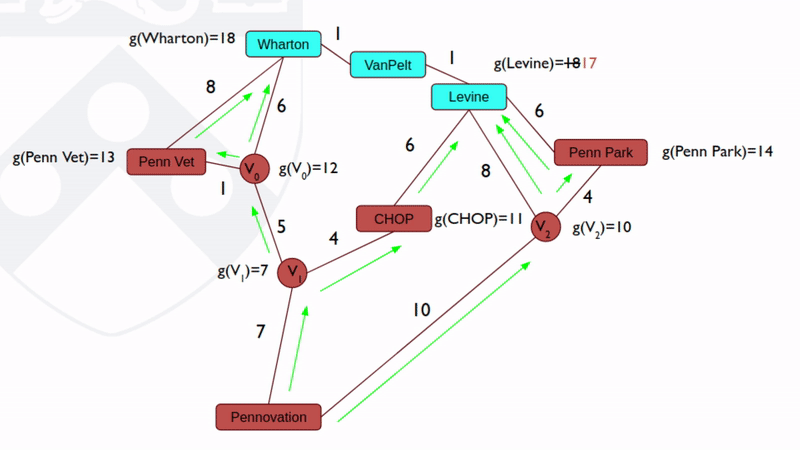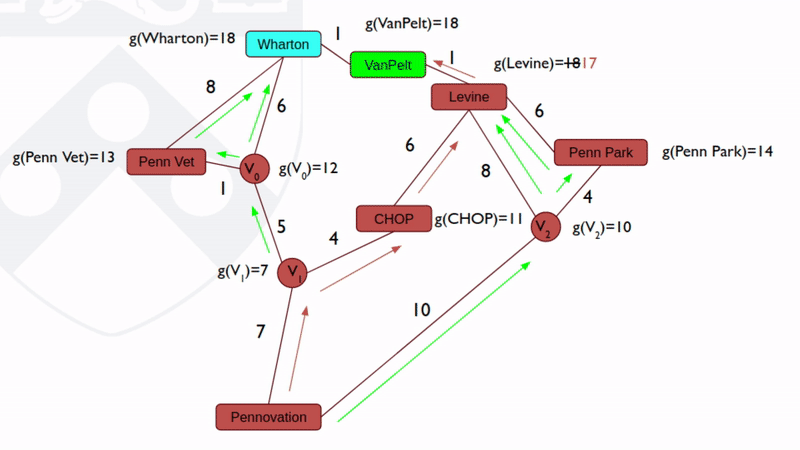
导航的核心任务是在地图上找到一条从起点到终点的路径,称为路径规划。最简单的路径规划是找到一条从起点到终点的“最短路径”。Dijkstra算法是一个经典的最短路径搜索算法。如图1所示,这一算法的基本思路是从起点开始,每次取当前所有路径中的最短路径进行扩展,并对扩展得到的节点更新其最短路径方案。这一扩展直到找到终点为止。
例如,如果当前的最短路径的终节点是A,那么扩展A到B;如果B以前没有被扩展过,那么由A扩展出的路径就是目前到达B的最短路径;否则就要比较一下由这条由A扩到B的新路径和原来记录的到B最短路径哪个更短,并选择更短的那条记录下来。这事实上是一个动态规划算法。
图1:Dijkstra 算法[1]
Dijkstra算法由波兰计算机学家Edsger W. Dijkstra 于 1956提出。这一算法是“精确”的,意思是如果起点和目标之间确实是连通的,那么肯定能找到一条路径,且这条路径一定是最短的。但是,Dijkstra算法的效率不高,如果图很大而起点和终点之间距离较远, Dijkstra算法会很慢,因为它要对很多节点进行扩展。例如我们想规划一条从北京到上海的最短路径,如果用Dijkstra算法来做,它几乎会把北京到周围城市的所有路径都找一遍,如图2所示。
图2:Dijkstra 算法效率较低 [2]
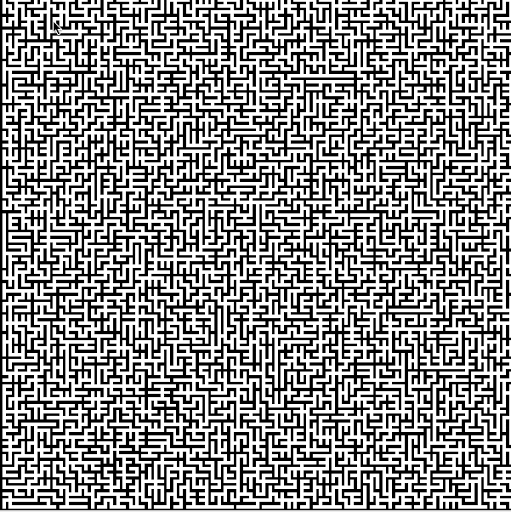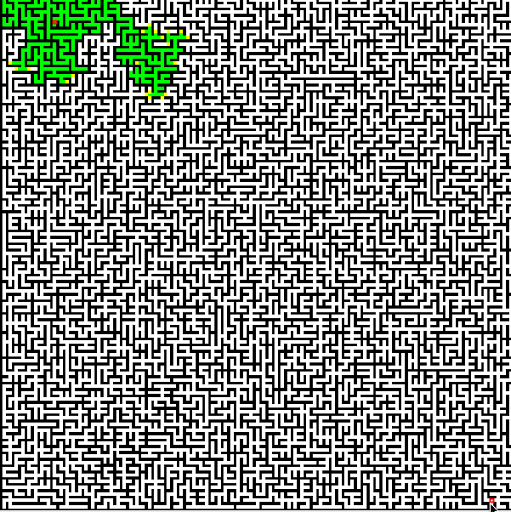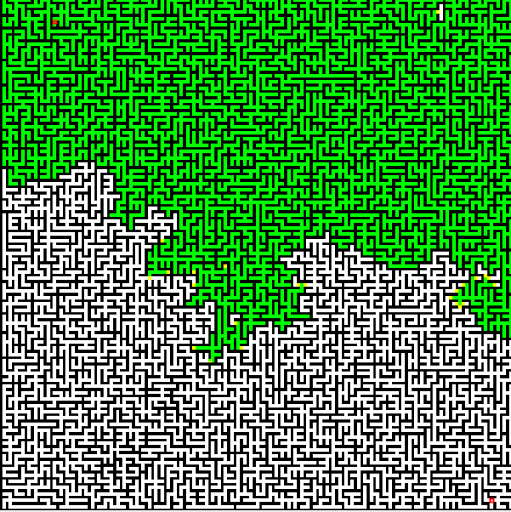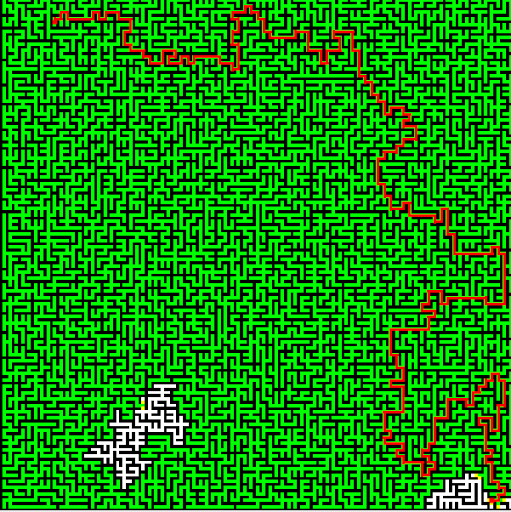
Dijkstra之所以效率不高,因为它是一种“盲目搜索”,在搜索时没有用到目的地信息,而是盲目地选择最短路径进行扩展。要用到目的地信息,可以从起始点和终点同时运行Dijkastra,直到他们在中间会师。还有一种办法是在搜索时考虑终点位置,选择那些往目的地靠近的节点进行扩展。
A*即是这样一种算法,它在选择扩展哪条路径时首先“估计”一下当前节点离终点的距离h,并将已经扩展的路径长度m和这个距离估计h加起来,选择h+m最小的路径进行扩展。算法中的h称为启发信息,这一信息指导算法始终往终点方向进行搜索。A*算法要求估计值h小于当前节点到终点的实际路径长度。研究表明,在这一条件下,算法找到的一定是最短路径。
图3:A* 算法效率较高 [3]
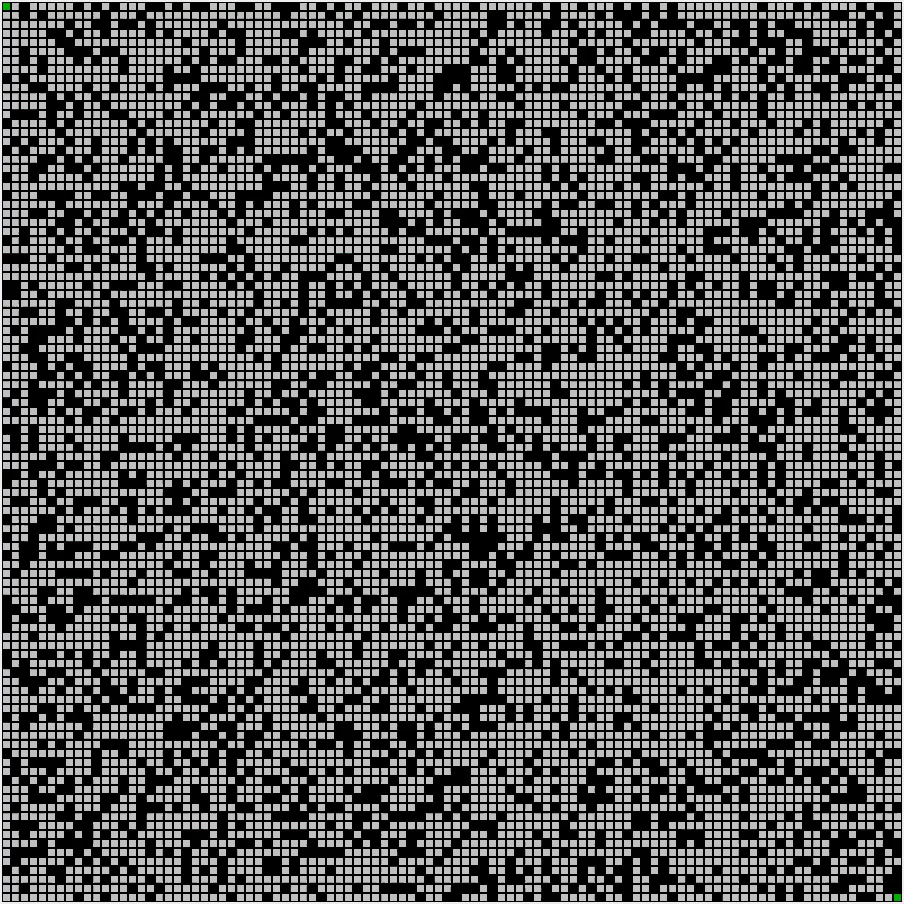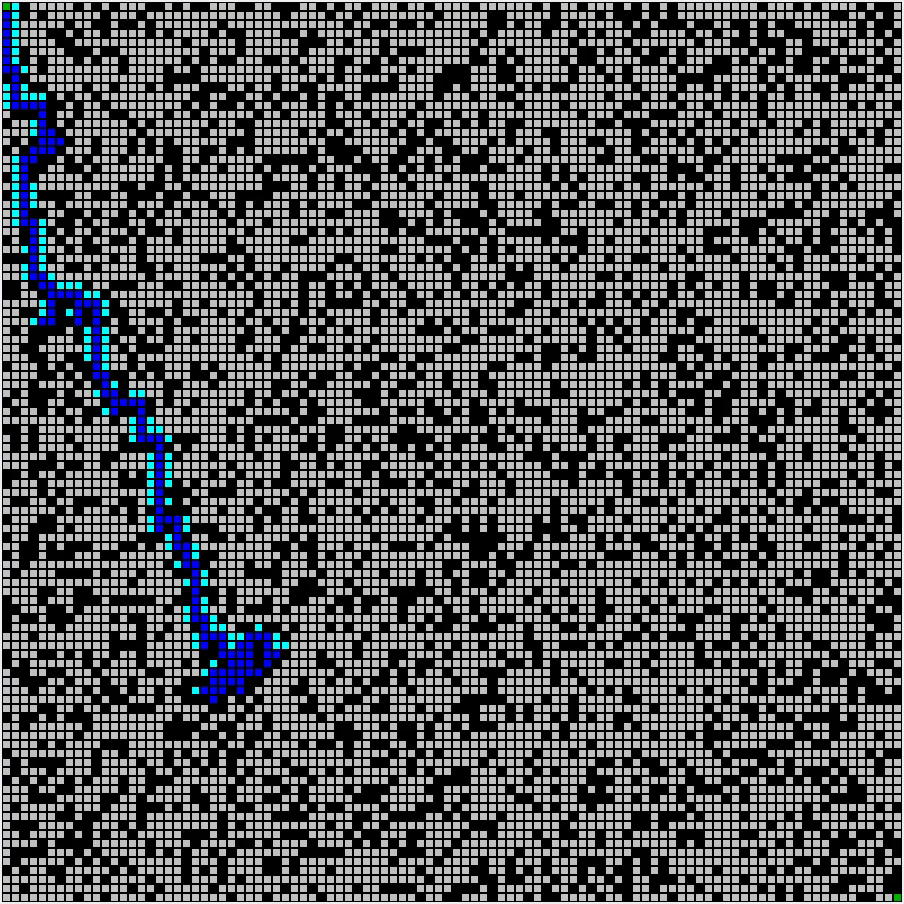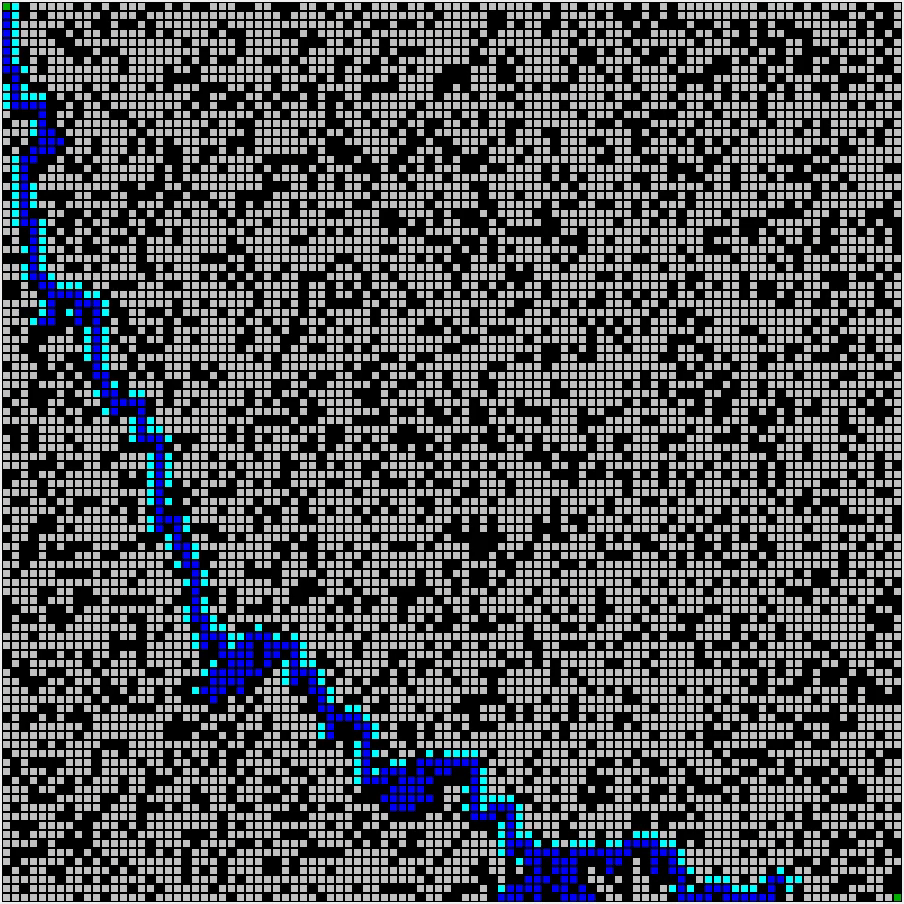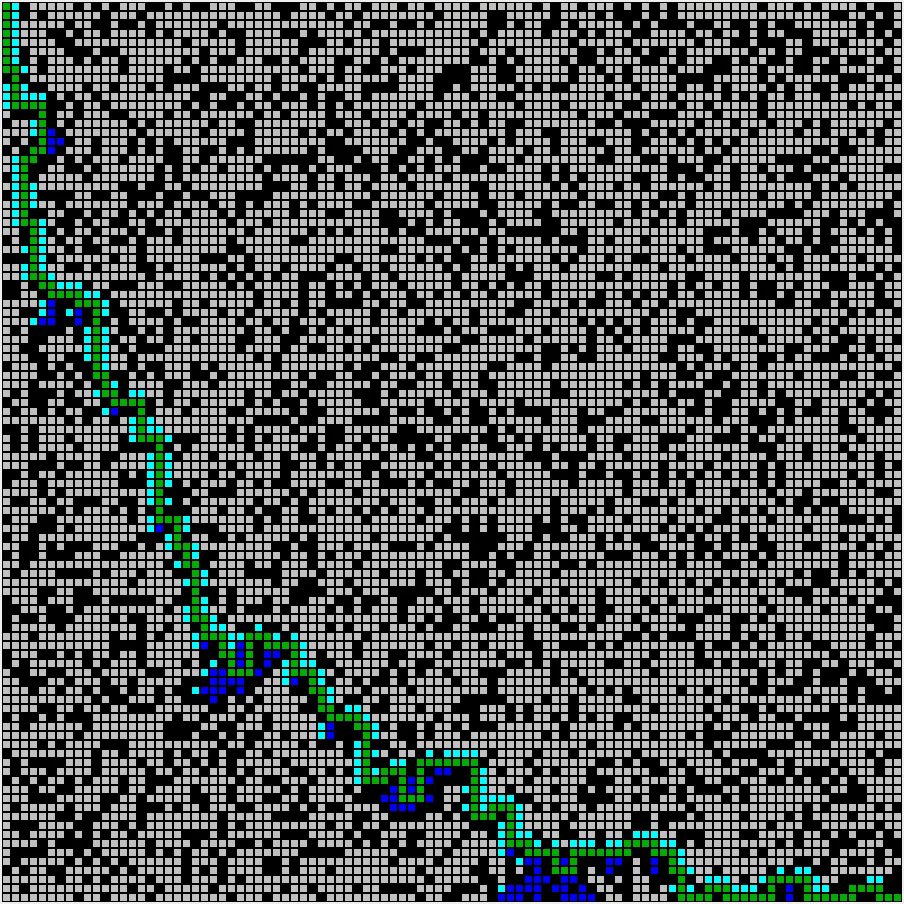
Dijkstra和A*只是基础算法,在实际导航系统中还需要做很多工作。比如如何对地图分层以实现快速规划;如何对热点目标的规划进行暂存,以供大量用户并发访问;如何加入用户需求,例如速度更快,红灯更少等;如何依路况即时更新路径;如何进行群体调度以平衡交通负载,开辟应急车道等等。总之,现在的导航系统已经不仅是人们出行的智能向导,还是一个可信赖的城市交通调度员。
参考文献:
[1]Motion Planning with F1/10, https://miro.medium.com/max/700/1*hDpECc95t4QizeB6fDXOuQ.gif
[2]https://lh6.googleusercontent.com/-nKFr72KsFfw/U4e6u41fb4I/AAAAAAAAAxg/IaM-X8CuVFU/551a4aed76904284b27b5b764d6412fd-2014-05-29-23-53.gif
[3]https://imgur.com/gallery/BS38gMt/comment/304144875
By:清华大学 王东
