支持向量机(Support Vector Machine, SVM)是一个非常特立独行的存在,它和符号学派不沾边,既不属于贝叶斯学派,也不属于连接学派,基本的假设就是样本离哪个类近,就属于哪个类。尽管假设如此简单,SVM却是机器学习中应用最广泛的分类器,在绝大多数任务中表现出优异的性能。
事实上,很少有一个模型能包含两种天才思想,SVM却是个例外,而这两个天才思想都是由Vladimir Vapnik本人或联合其他合作者提出的,不得不说Vapnik是天才中的天才。
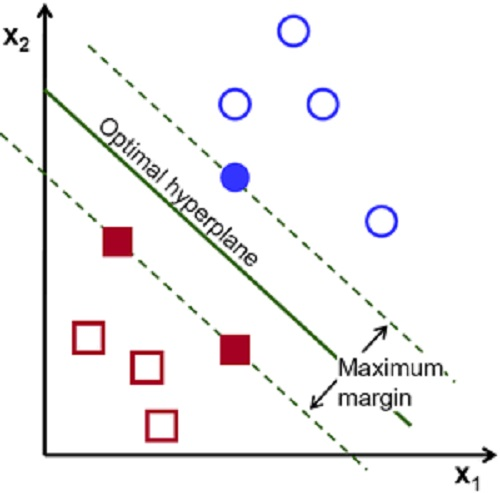
1963年,Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis首先提出了第一个天才思想,后人称之为“最大边界准则”。如图1所示,我们的目的是要找一条直线将蓝圈和红框分开,怎么做呢?Vapnik建议这样:首先找到每一类中离分类面最近的点,这些点到分类面的距离称为“边界”,然后想办法调整分类面,使得边界越来越大。换句话说,“让最近的点越远越好”, 这就是“最大边界准则”。看起来似乎很自然,但这一准则的内涵却非常深刻。
列举几点如下:
(1)我们在选择分类面时,只需考虑边界上的点,类内的点则不需考虑。换句话说,SVM是“捡硬柿子捏”的,硬柿子都捏了,软柿子就更不在话下。因此,SVM具有天然的鲁棒性;
(2)只考虑边界点意味着SVM不受数据分布假设的限制,因而可应用于分布复杂的真实数据;
(3)只考虑边界点使得训练不受训练样本量的影响,因而对类间的数据不均衡具有天然鲁棒性。
图1:SVM模型最大化两类的边界
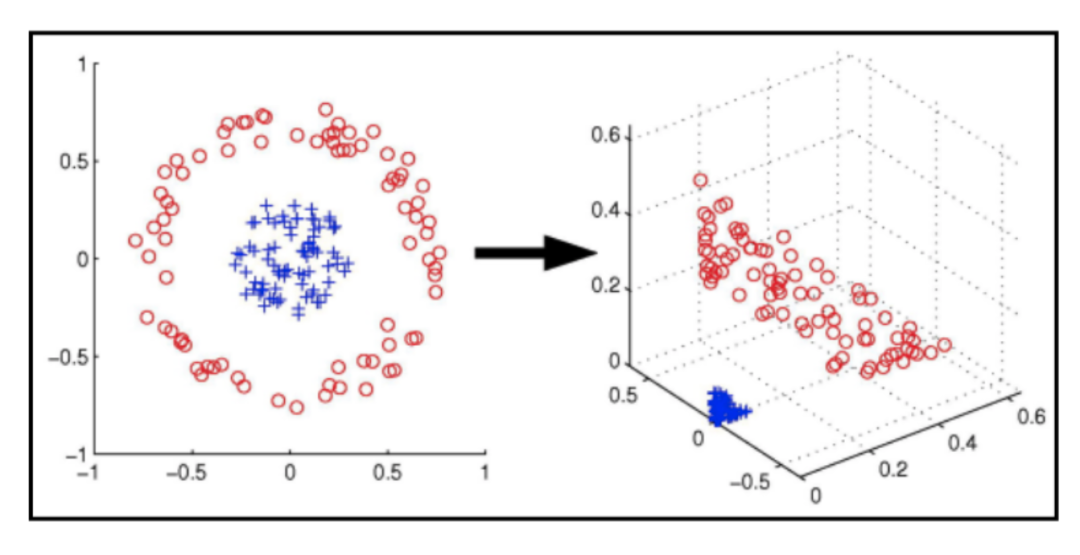
1992年,Bernhard Boser, Isabelle Guyon and Vladimir Vapnik等人提出了第二个天才思想,后人称之为“核方法”。我们知道数据如果比较复杂的话,线性模型是无法实现合理分类的。如图2左图所示,一类数据围绕在另一类数据周围,这时无法找到一个线性模型将这两类分开。一种办法是用一个非线性映射将数据映射到一个高维特征空间,并在该空间中训练线性分类器,如图2中右图所示。
图2
如何得到这个非线性映射呢?Vapnik采用了一种非常新奇的思路:设计一个“核函数”k(x,y),使其等价于x,y经过某一特征φ映射后的内积,即k(x,y)= <φ(x) ,φ(y)>。基于这一关系,即可将数据空间中的非线性建模问题归结为特征空间中的线性建模问题。值得说明的是,我们只需知道核函数k(x,y)隐性定义了某一映射φ,但并不需要获得φ的具体形式,因为所有计算都是基于k(x,y)进行的。
利用核函数来定义映射是个非常有趣的思路,一是核函数对关系的定义相对直观、简单,且有很多先验知识可用;二是通过定义核函数可以得到非常复杂的映射,从而把数据映射到极高维度的特征空间甚至是无穷维空间,极大提高了模型的表达能力;第三,也是最重要的,即便核函数定义的再复杂,在映射空间中建立的依然是线性模型,因此依然可得到全局最优解。保持训练过程的全局可优化是核方法对神经网络模型的最大优势。
核方法极大扩展了SVM模型的建模能力,使SVM的性能大幅提高。1993年,Corinna Cortes 和 Vapnik引入松驰变量来处理错分类的训练样本,进一步扩展了SVM模型,奠定了目前广泛使用的SVM模型的基础。值得说明的是,SVM中的两大思想--最大边界和核方法--是互相独立的,各自都有广泛应用。
By:清华大学 王东
